正準相関分析 CCA を用いた図書推薦

https://www.kaggle.com/ruchi798/bookcrossing-dataset
に公開されているデータのうち、Preprocessed_data.csv を利用して、正準相関分析の練習を行う。

データクレンジング

Preprocessed_data.csv には非常に多くのデータが登録されており、全件を使うと非常に大変（というか、CCAで処理しきれない）なので、データ量を削減する。

import pandas as pd

df = pd.read_csv("Preprocessed_data.csv")

# 読者に関する情報の整理：アメリカに在住している50歳以下のみを対象とする
df = df[df.age <= 50]
df = df[df.country=="usa"]
df = df[~df.city.isnull()] #住んでいる都市が登録されている人に限定

# 新しい書籍に注目する
df = df[df.year_of_publication >= 1985]

# 高レーティングになっているものに注目する
df = df[df.rating >= 8]

ついでに、少しデータを処理しやすくする。Category列は配列を文字列化したような構造になっているものの、全ての書籍で1つのカテゴリしか割り当てられていないので、単なる文字列に加工する。

df.Category = df.Category.apply(lambda s: s[2:-2]) # ['fiction'] -> fiction
df = df[df.Category != ""] # Category == "9" となっているデータが存在している

これでもまだデータ件数が多すぎるため、より沢山の書評を行っている人、より沢山の書評を受けている書籍を選抜する。

# 書評を書いたtop 100 人を選抜
top_users = list(df.user_id.value_counts()[:100].index)
df = df[df.user_id.apply(lambda x: x in top_users)]

# top 100 人に沢山読まれた top 100 冊を選抜
top_books = list(df.isbn.value_counts()[:100].index)
df = df[df.isbn.apply(lambda x: x in top_books)]

# あとでindexがずれていると困るので、indexを0スタートに修正
df.reset_index(inplace=True, drop=True)

これを解析の対象とする。

正準相関分析 (CCA) のためのデータ準備

このデータセットには様々な文字列情報が含まれているが、CCAは行列に基づく手法であるから、数値しか扱うことができない。ここでは、用いる特徴量を絞り、さらに文字列情報についてone-hot encodingなどの処理を行うことでCCA実行可能な状態にする。

まず、今回用いる情報を抜き出す。

df_users = df[["user_id", "age", "city"]]
df_books = df[["isbn", "year_of_publication", "Summary"]]

もちろん、user_idやisbnには学習すべき情報は含まれない（その人やその本の性質はこれらの情報には含まれていないはずだ）。したがって、学習にはさらに情報を絞る必要がある。

df_users_cca = df_users[["age", "city"]]
df_books_cca = df_books[["year_of_publication", "Summary"]]

続いて、文字列情報の数値化を行う。今回のデータでは、city, Summary が文字列情報に該当する。cityはその人の在住する都市であり、必ず1つに定まる。one-hot encodingをすれば良さそうである。一方、Summaryはその書籍概要文であるから、文章となっている。これをone-hot encodingすると、書籍ごとに異なるone-hotとなってしまうだろう（全く同一の概要になる書籍はおそらく存在しない）。こちらについては、bag-of-words（出現する単語をカウント）を用いることにする。

# cityのone-hot encoding
df_users_cca = pd.get_dummies(df_users_cca, columns=["city"])

# Summaryのbag-of-words生成
from sklearn.feature_extraction.text import CountVectorizer
cnt = CountVectorizer()
bag_of_words = cnt.fit_transform(df_books_cca.Summary)
df_bag_of_words = pd.DataFrame(bag_of_words.toarray(), columns=cnt.get_feature_names())
df_books_cca = pd.concat([df_books_cca[["year_of_publication"]], df_bag_of_words], axis=1) # 横方向に結合

これで、数値だけからなるデータが作成された。それぞれの次元を見てみよう。

print(df_books_cca.shape) # -> (804, 1010)
print(df_users_cca.shape) # -> (804, 87)

このことから、804件の rating >= 8 の書評が選ばれたことがわかり、書籍に関しては1010次元、読者に関しては87次元で表現されていることがわかる。

正準相関分析 (CCA) の実行

ここまでで準備したデータを用いて、正準相関分析を行ってみる。

from sklearn.cross_decomposition import CCA

X = df_users_cca.values
Z = df_books_cca.values

cca = CCA(n_components=2)
cca.fit(X, Z) # それぞれ2次元に射影

これで正準相関分析を実行できる（相変わらず、機械学習の実行部分はあっけない）。結果を可視化してみる。

import numpy as np
import matplotlib.pyplot as plt
def plot(X, c=None, title=None, cbar=True):
    plt.figure(figsize=(5,5))

    plt.scatter(X[:,0], X[:,1], cmap=plt.cm.rainbow, c=c)
    if cbar:
        plt.colorbar()
    plt.title(title)
    plt.show()

# 重複を除去したものをtransformする
X_uniq, X_uniq_ind = np.unique(X, axis=0, return_index=True)
Z_uniq, Z_uniq_ind = np.unique(Z, axis=0, return_index=True)
Xc, Zc = cca.transform(X_uniq, Z_uniq)

# X_uniq_ind, Z_uniq_ind を使って、dfについてもunique処理を行う
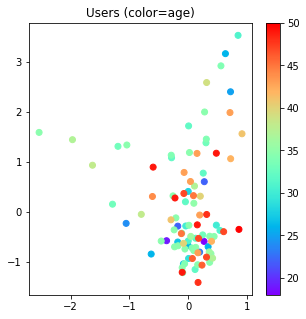
plot(Xc, title="Users (color=age)", 
     c=df_users_cca.iloc[X_uniq_ind].age)
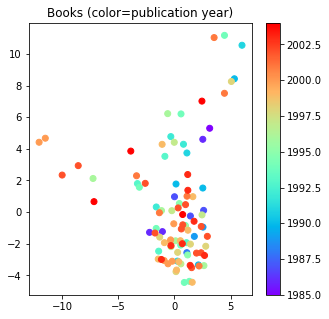
plot(Zc, title="Books (color=publication year)", 
     c=df_books_cca.iloc[Z_uniq_ind].year_of_publication)

結果はこのようになった。少なくとも読者、書籍の広がりが類似していることから、適切に書評関係がある人ー書籍がこの射影された空間で近づくように学習されているように見える（実際に書評関係のある読者ー書籍ペアがこの射影空間上でどのくらいの距離になっているのかを確認すると良いだろう）。

正準相関分析の結果を用いた書籍推薦

CCAは単なる行列による射影、すなわち $\boldsymbol{A}$と$\boldsymbol{B}$をそれぞれ行列として$ \boldsymbol{X}_c = \boldsymbol{A}\boldsymbol{X} $, $\boldsymbol{Z}_c = \boldsymbol{B}\boldsymbol{Z}$ と変換しているだけなので、似た性質を持つ読者 $\boldsymbol{x}_1$, $\boldsymbol{x}_2$はこの射影された空間においても近接するはずである。
この性質と、高レーティングの書評を付けた人ー書籍の関係がこの空間で近接することを利用すると、
射影された空間で近接している読者＆書籍は高レートを付ける可能性が高いと考えることができる。

今回はテストケースとして、Xc[10]の人について、次に推薦する書籍を考えてみることにする。もちろん、すでに書評を付けている書籍を推薦しても仕方がないので、まだ書評関係が存在していない書籍について抜き出す必要があることに注意する。

target = Xc[10]
dists = np.linalg.norm(Xc[10]-Zc, axis=1) #ブロードキャストを利用
near_ind = dists.argsort() # 射影空間上での距離が近い順に書籍のindexを取得

# 射影空間上での距離が近い順に並べられた書籍リストを作成
df_books_uniq = df_books.iloc[Z_uniq_ind]
df_near_books = df_books_uniq.iloc[near_ind]

# 読者の書評リストを作成
target_user_id = df_users.iloc[X_uniq_ind[10]].user_id 
df_target = df[(df.user_id == target_user_id)]

# 書評リストに存在しないisbnを、近接順に列挙
df_near_books = df_near_books[df_near_books.isbn.apply(lambda s: s not in df_target.isbn)]

この結果によると、isbn = 0446608955 の書籍が次に読んでほしい書籍のようだ。書籍名は"A Walk to Remember" と登録されており、Fictionのようである。 この読者は過去に高レーティングを付けた書籍はFictionのみであり、この書籍推薦は悪くなさそうである。