はじめに
超新星残骸の粒子加速理論をざっと整理してみる。まずは、圧縮した要約から紹介してみます。
(注) この記事は、SNRの基礎やHT系など、下記の記事の内容は前提になっています。
■ 粒子加速の最短サマリ
まず、議論を明確にするために座標系を固定します。
一般性を失うことなく、以下のように座標軸をとります:
- x 軸:衝撃波の法線方向(shock normal direction)
- y 軸:衝撃波面内の代表方向(in-plane direction)
- 磁場 $\mathbf{B}$ が x 軸に平行なら parallel shock
- 磁場 $\mathbf{B}$ が x 軸に垂直なら perpendicular shock
この定義だけで、どちらの加速機構も整理できます。
■ 粒子加速の本質:
「反転する速度成分」と「動く壁の方向」が一致すると加速が強くなる
● 1. Diffusive Shock Acceleration(DSA:拡散衝撃波加速)
(いわゆるフェルミ加速)
- 粒子が衝撃波で散乱されると、法線方向の速度成分 $v_x$ が反転する。
- 衝撃波という“動く壁”も、法線方向(x 方向) へ進んでいる。
→ parallel shock(磁場が法線方向)で最も効率的に加速が起こる。
● 2. Shock Drift Acceleration(SDA:衝撃波ドリフト加速)
(de Hoffmann–Teller 系での記述)
- HT 系に移ると粒子は磁場でミラー反射し、
反転するのは 衝撃波面内の速度成分 $v_y$。 - HT 系の“動く壁”の速度($v_{\mathrm{HT}}$)も、
衝撃波面内(y 方向) に向いている。
→ perpendicular shock(磁場が衝撃波面に寝ている配置)で加速効率が最大。
■ 一行でまとめると:
加速が強いのは、粒子の「符号が反転する速度成分」と、加速を生む「動く壁の速度」が同じ方向にあるときである。
- parallel shock → DSA が効率最大
- perpendicular shock → SDA が効率最大
■ 表でまとめると:衝撃波角の依存性
| 加速メカニズム | 反射で変わる速度 | “動く壁”の方向 | 効率最大の角度 |
|---|---|---|---|
| DSA | vₓ(法線) | 法線方向 | parallel |
| SDA / HT | vᵧ(面内) | 面内方向 | perpendicular |
“parallel shock は DSAに強い、perpendicular shock は SDAに強い”
という教科書的事実の根っこは、反射で変わる速度成分と、加速に効く壁の速度方向が一致するかどうか。
補足説明 : 反射で符号が変わる速度成分”と“動く壁の速度”の関係
「符号が変わる速度成分 × 動く壁の速度」 の一致性
粒子が衝撃波でエネルギーを得る仕組みは、フェルミ型(壁との弾性衝突) と同じ構造を持つ。フェルミ加速のエネルギー増加は、
\Delta E \sim 2 m v_{\rm rel} V_{\rm wall}
のように
「反射で反転する速度成分(=壁に向かう成分)」
×
「壁の速度」
で決まる。
ここで重要なのは、どの方向の速度成分が反射で符号反転するかである。
● 1. 反射で符号が変わる成分=“鏡”に向かう成分
粒子が磁場によって鏡面反射されるとき、符号が反転するのは“鏡面に直交する成分” だけである。
-
DSA の場合:衝撃波法線方向 $x$ が反転
→ 反転するのは vₓ -
SDA の場合:ショック面内方向 $y$ に沿った磁力線鏡で反転
→ 反転するのは vᵧ
つまり、加速に関わる“速度成分”は角度 θ_Bn で決まる。
● 2. 加速に効く“動く壁の速度”も方向を持つ
衝撃波そのもの、または HT frame での仮想的な壁(mirror)は、特定方向に速度を持って動く壁とみなせる。
| 加速機構 | “動く壁” | 壁の速度方向 |
|---|---|---|
| DSA | 衝撃波面(upstream → downstream) | 法線方向(x) |
| SDA/HT | HT frame の仮想的 mirror | 面内方向(y) |
● 3. 加速が大きいのは、反転成分の方向 = 壁速度の方向 のとき
フェルミ型のエネルギー増加は壁に向かって飛び込んだ速度成分が反転し、壁の動きと合成速度が増えることで起きる。
よって、
\textbf{反転する速度成分の向き} \quad = \quad
\textbf{壁の速度の向き}
が一致すると、
往復ごとのエネルギーゲインが最大化する。
● 4. これを衝撃波角 θ_Bn に対応づけると:
◆ parallel shock(θ_Bn ≈ 0°)
- 反転するのは vₓ(法線方向)
- 壁の速度 U₁ も 法線方向
→ 一致する → DSA が強く働く
◆ perpendicular shock(θ_Bn ≈ 90°)
- 反転するのは vᵧ(面内方向)
- HT frame の速度 v_HT (= U₁ tanθ_Bn) も 面内方向
→ 一致する → SDA が強く働く
● 5. 結論
粒子加速角度依存の本質は、
✔ 「反射で符号が変わる速度成分」
✔ 「加速に影響する“壁”の運動方向」
この 2 方向が一致したときだけ
フェルミ型の「壁との衝突」でエネルギーが増えるからである。
\Delta E \propto v_{\rm flip} \times V_{\rm wall}
が最大になる角度が、“その加速機構が最も効率良く働く衝撃波角”になる。
このような理解を踏まえた上で、近年の動向を整理してみましょう。
1. ざっくり全体像:何を「近年の進展」と見るか
従来:
- イオンについては
→ Caprioli & Spitkovsky 型のハイブリッド計算で
「準平行ショックがエネルギー変換効率(CR への総エネルギー)が高い」
というのが一つの大きな流れ。
- 一方で、電子の「注入問題」― DSA に乗せる前にどうやって数百 keV〜MeV まで持ち上げるか ― は長く未解決だった。
そこに対して、
[1] 高 Mach 数準垂直ショックの PIC 計算で 電子の二段階加速(Shock Surfing Acceleration → Shock Drift Acceleration) を提案・定量化し、SNR 条件で十分な電子注入が起こり得ることを示した。
"Electron Injection at High Mach Number Quasi-Perpendicular Shocks : Surfing and Drift Acceleration", The Astrophysical Journal, Volume 690, Issue 1, pp. 244-251 (2009).
Amano Takanobu, Hoshino Masahiro
[2] さらに、従来の SDA を乱流込みで一般化した Stochastic Shock Drift Acceleration (SSDA) を理論構築し、そのスペクトルを解析的に出した。PIC計算も様々進展する。
[3] その SSDA を地球衝撃波(MMS 観測)で直接検証が示された。
[4] そして 2022 年のレビュー論文で、準垂直ショックにおける電子加速を「SSA+SSDA+Weibel 支配ショック+磁気リコネクション」という枠組みに整理した。
という流れになっています。
以下、少し丁寧に分解します。
2. 2006〜2013:高 Mach 数準垂直ショックでの電子注入機構(SSA→SDA)
(1) Amano & Hoshino (2006):二段階モデル SSA→SDA
Amano & Hoshino (2006) は 1D PIC で 高 Mach 数準垂直ショック を計算し、電子注入を以下の二段階で説明しました:
[1] ⚡ Shock Surfing Acceleration (SSA)
- ショックで、反射イオンと入射電子の流れの差から Buneman 不安定性が起こり、静電波が立つ。
- 電子はこの静電ポテンシャル井戸に「サーフィン」して、磁場にほぼ垂直方向に一気に加速される。
Buneman 不安定性とは、衝撃波のフット部などで反射イオンと入射電子の間に十分な速度差があるときに励起される静電的な不安定性であり、電子が形成された電位井戸に捕捉されて「サーフィン」するように急加速される機構(SSA: Shock Surfing Acceleration)の駆動源となります。この不安定性は、電子のドリフト速度が熱速度を超える条件で成長しやすく、PIC 計算においても確認されています(例:Amano & Hoshino 2007, arXiv:astro-ph/0612204)。詳しい導出や条件については、該当論文や標準的なプラズマ物理の教科書をご参照ください。
衝撃波のフット部では、反射イオンと入射電子の流れ速度の差 $\Delta v$ により、Buneman 不安定性が励起されます。これにより生成される静電ポテンシャル $\phi(x)$ に電子が捕捉され、以下の式で表される電場 $E = -\nabla \phi$ により加速されます:
\frac{d\boldsymbol{p}}{dt} = -e \boldsymbol{E}
電子はこのポテンシャル井戸を 「サーフィン」 する形で運動し、磁場とほぼ垂直方向に一気に加速されます。典型的には、
\Delta \mathcal{E}_{\rm SSA} \sim e \phi_{\rm max}
で、$\phi_{\rm max}$ はBuneman波によるポテンシャル深さです。
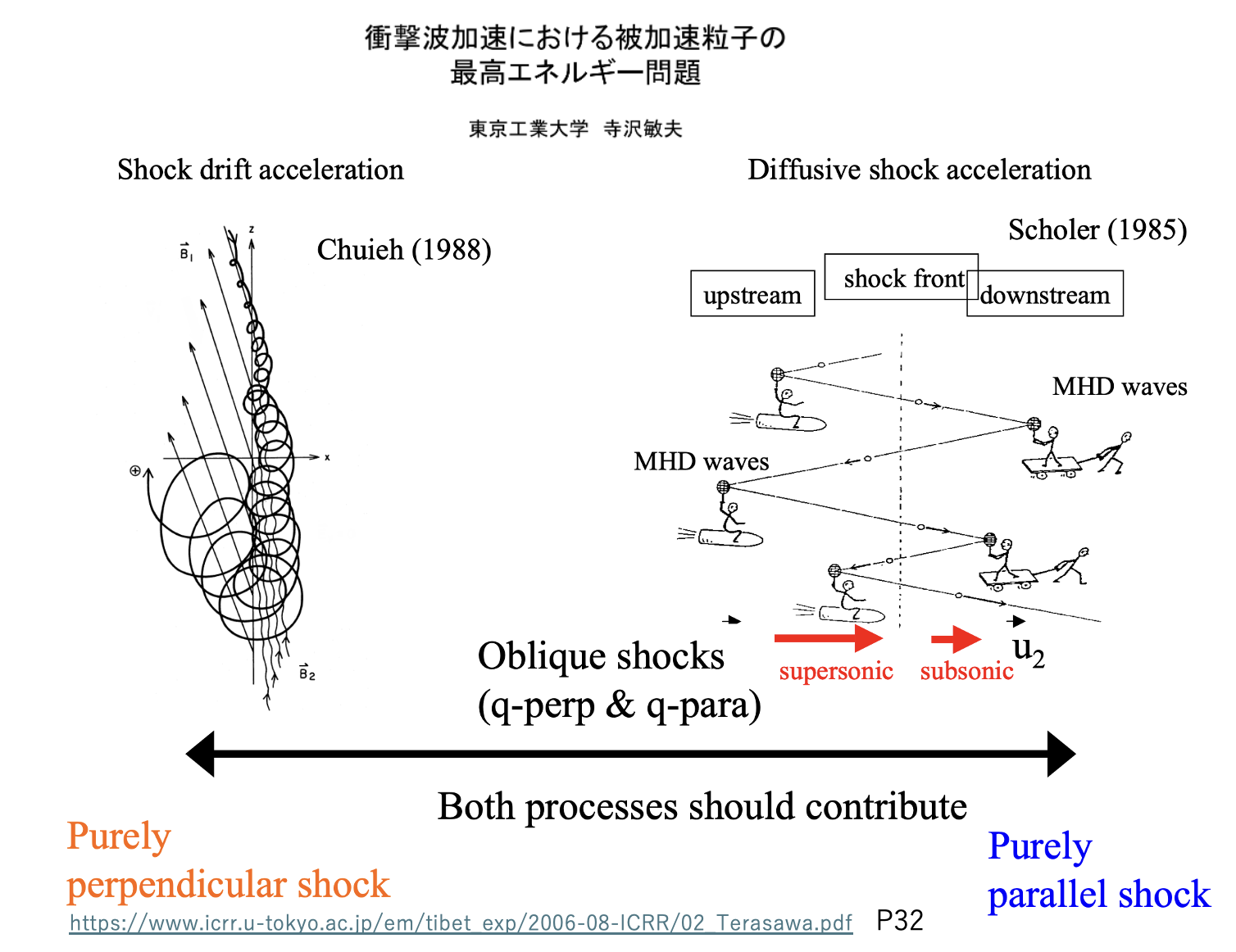
(補足)専門的な説明
専門的に深く知りたい方向けには、2006年の寺沢先生のスライド、
「衝撃波加速における被加速粒子の最高エネルギー問題」 東京工業大学 寺沢敏夫
などご参考ください。
[2] 🔁 Shock Drift Acceleration (SDA)
- SSA である程度高エネルギーになった電子は、ショック面での磁場勾配に沿ったドリフト運動をしながら、モーション電場からさらに仕事を受ける。
- その結果、一部の電子は上流方向へ反射され、DSA に注入可能なエネルギー帯に到達する。
SSA で初期加速された電子は、ショック面での磁場勾配 $\nabla B$ によるミラー反射と、ドリフト運動を通じてさらにエネルギーを得ます。電子のドリフト速度は
\boldsymbol{v}_D = \frac{m v_\perp^2}{2 q B^2} (\boldsymbol{B} \times \nabla B)
で与えられ、この速度でモーション電場 $\boldsymbol{E} = -\boldsymbol{v}_{\rm sh} \times \boldsymbol{B}$ から仕事を受け、エネルギーが増加します:
\frac{d\mathcal{E}}{dt} = -e \boldsymbol{v}_D \cdot \boldsymbol{E}
このように、SSA→SDA の二段階はそれぞれ:
- SSA:静電場による初期急加速($\sim$ $\phi$)
- SDA:磁場勾配によるドリフト加速($\sim$ $\nabla B$)
という異なるメカニズムで電子を加速します。
(2) Matsumoto, Amano & Hoshino (2013):超高 M_A での PIC
その後、Matsumoto et al. (2013, ApJ/PRL) は Alfvén Mach 数 $M_A \sim 45$ の非相対論ショックを 2D PIC で計算し、
- ショックのフット部での Buneman・ion-acoustic、ショック内部での ion-Weibel など、複数の不安定性が空間的に分離して動作すること、
- SSA により MeV 級までの電子が作られ、Weibel 乱流と組み合わさってさらにエネルギーが伸びること
を示しました。
「高 Mach 数 SNR ショックでは、準垂直でも「内部はかなりガチャガチャな Weibel 乱流+電場・磁場構造」 になっていて、1D de Hoffmann–Teller picture では捉えきれない」というメッセージではないかと。
3. 2017:Weibel 支配ショックと 3D SSA+SDA(Matsumoto+ 2017)
Matsumoto et al. (2017, PRL) は、さらに一歩進んで 3D PIC で
「Weibel 支配の高 Mach 数準垂直ショックで、電子がどうやって relativistic まで行くか」
を調べました。
主な結果は:
- ショックフット部で強い Buneman 波 → SSA による初期加速
- ショック内部で self-generated な ion-Weibel 乱流
→ 電子はこの乱流によるピッチ角散乱を受けながら、
ショック面に沿って ドリフトしつつ何度も加速される(stochastic drift) - 結果として、
SSA でシードを作り、続くドリフト+乱流散乱で「確率過程としての SDA」に近い振る舞いをする
この「Weibel 支配ショック」という概念がその後のレビューにも引き継がれていて、
$M_A$ も音速 Mach 数も 20–40 を超えるような超高 Mach 数ショックでは、
上流の磁場は「弱い背景」でしかなく、ショック自体が自分で作った Weibel 磁場に支配される
という描像が提案されています。若い SNR はまさにこのレジームに入る可能性が高い。
4. 2019–2020:Stochastic Shock Drift Acceleration (SSDA) とその観測検証
(1) Katou & Amano (2019):SSDA の理論
Katou & Amano (2019, ApJ 874, 119) は、
従来の SDA を
ショック遷移層内でのピッチ角散乱を取り入れた「確率過程」として一般化
し、これを Stochastic Shock Drift Acceleration (SSDA) と名付けました。
理論的には:
- ショック面近傍の遷移層を一種の「加速領域」とみなし、
- 粒子のエネルギー $E$ と滞在時間の確率分布を記述する輸送方程式を解くと、
-
強い散乱の極限で、定常状態のエネルギースペクトルはパワーローになる
(→ DSA 的な $dN/dE \propto E^{-p}$ の形)。
要は、先述の Matsumoto 3D 計算で見えていたような「SSA された電子が乱流とドリフトの中を何度も回りながら加速される」プロセスを、きちんと Fokker–Planck 的にモデル化したものと考えてよいのでしょう。
(2) Amano et al. (2020):MMS による SSDA の直接検証
Amano et al. (2020, PRL 124, 065101) は、地球ボウショックの MMS 観測から
- ショック面に沿った電子のドリフト運動、
- 遷移層での乱流・散乱、
- それによるエネルギー分布のパワーロー
を解析し、SSDA モデルが実観測の電子スペクトルを非常によく再現することを示しました。
MMS(Magnetospheric Multiscale Mission) は、NASA が 2015 年に打ち上げた 4機編隊の宇宙探査機による科学ミッションで、地球の磁気圏で起こる 磁気リコネクション、衝撃波、乱流 などのプラズマ現象を、電子スケールの微細構造まで直接観測することを目的としています。磁気圏で起こる現象は、時間変化が速く、空間構造も小さいため、1 機だけでは「空間変化」と「時間変化」が区別できません。MMS は 4 機をテトラヘドロン(四面体)型で編隊飛行させることで、ある瞬間の 三次元構造その後の時間変化を同時に捉えることができます。
ここでうれしいのは、
「理論(SSDA)→ PIC → 宇宙機観測(MMS)」
という三角形が閉じていて、
「じゃあ若い SNR の準垂直ショックでも、似たメカニズムで電子の注入が起こっている??」
と考えられるようになってきた、という点です。
5. 2022 レビュー:準垂直ショック電子加速の「統一図」(Amano+ Matsumoto+ Bohdan 他)
Amano, Matsumoto, Bohdan らによる 2022 年のレビュー論文(Nonthermal Electron Acceleration at Collisionless Quasi-perpendicular Shocks)は、ここまでの流れをかなりきれいに整理しています。
簡単に整理すると、準垂直ショックを
-
SSDA:中〜高 Mach 数、ある程度磁化された準垂直ショック
- SDA + ピッチ角散乱 → ショック遷移層内でパワーロー的電子加速
- MMS や衛星観測と対応
-
SSA (Shock Surfing Acceleration):高 Mach 数での Buneman 由来の静電波による初期加速
- SSA → SSDA/DSA への「射出」の役割
-
Weibel 支配ショック:超高 Mach 数で上流磁場が弱い場合
- Ion-Weibel 乱流 + 自発的磁気リコネクション
- 電子は SSA に始まり、乱流中での stochastic drift + reconnection でさらに加速
という三つのレジームに分けて議論し、準垂直ショックでも、電子は十分な注入と加速が可能である(ただし、どのメカニズムが主役かは Mach 数・β・obliquity で変わる)という統一的な絵を描いています。
6. 「準平行 vs 準垂直」像はどうアップデートされたか?
これまでの話(Caprioli & Spitkovsky など)と合わせて、現在のイメージをまとめると:
-
イオン(陽子)主導の CR エネルギー変換効率
-
準平行ショックで
- 反射イオン → 自己励起 Alfvén/Bell 波 → 強い磁場増幅
- DSA が効率よくまわり、SNR のバルクエネルギーの 10–20% を CR に変換しうる
-
準垂直ショックでは、イオンの上流反射と自己励起乱れが弱く、イオン DSA はあまり効かない。
-
-
電子の「注入と初期加速」
-
準平行でも高 Mach 数ではかなり効くことが bow shock 観測などから示唆されているが
-
特に 準垂直ショック + 高 Mach 数 では、
- SSA + SSDA + Weibel 乱流 + reconnection の組み合わせで
電子の非熱成分が高い効率で生成されうることを Amano & Matsumoto 系の仕事が示している
- SSA + SSDA + Weibel 乱流 + reconnection の組み合わせで
-
-
結果として:「どちらが効率か?」
- イオンのエネルギー変換効率で考えると? → 準平行が勝ち(Caprioli et al. etc.)
-
電子の注入・初期加速能力で考えると? → 高 Mach 数準垂直もかなり強力
Amano/Matsumoto らの結果では Weibel 支配レジームでむしろ「電子は準垂直ショックの方が加速されうる」
という二面構造になっている、というのが近年の整理だと思います。
7. まとめ
ハイブリッド計算(e.g., Caprioli & Spitkovsky ら)により、若い SNR でイオンを効率よく加速するのは主に準平行ショックであることが示された。一方で、電子の注入機構は長らく未解決問題として残っていた。天野・松本らの一連の PIC/理論研究は、準垂直かつ高 Mach 数ショックにおいて、Buneman 不安定性に基づく shock surfing acceleration(SSA)と、乱流とドリフト運動を組み合わせた stochastic shock drift acceleration(SSDA)が連続的に働くことで、電子を DSA に注入可能なエネルギーまで効率良く引き上げ得ることを示し、その理論を地球ボウショックの観測で検証した。さらに Weibel 支配ショックという新たなレジームを提示し、SNR 条件では準平行ショックがイオンの主加速を担い、準垂直ショックが電子の注入・初期加速で重要な役割を果たすという、より精緻な幾何学依存像を与えつつあり、観測との比較においては、磁場の配向が効いてくるので、高空間分解能による偏光観測の進展が突破口になるのであろうか、、という感じだと思います。
参考文献
- 論文
- Qiita関連記事