1. はじめに:1次元最適化とminimize_scalar(bounded)
SciPy の scipy.optimize.minimize_scalar は、1変数関数の最小化を行う定番ツールである。特に
minimize_scalar(method="bounded")
は、探索区間 $[a,b]$ を明示できるため
- 物理パラメータの制約(正値、範囲制限)
- 統計推定(最尤推定:MLE)
- コスト関数最小化(設計最適化)
に対して 堅牢で安全に使える。
ただし、現場で重要になるのはここである:
-
success=Trueは何を意味する? - 得られた解は本当に極小か?
- その誤差バーは妥当か?
- “局所の曲率”だけで誤差を見積もっていないか?
本記事は
数学(Brent法) → 物理(安定点) → 統計(尤度) → 実装(検証作法) → 誤差評価
という順番で、minimize_scalar(bounded) を 論文・レビューに耐える形で使うための実務テンプレを提示してみたいと思います。
scipy.optimize.minimize と minimize_scalar の違い
その前に、scipyの次の2つの違いだけは説明しておきます。
-
minimize_scalar→ 1次元専用の、安全で堅牢な最適化 -
minimize→ 多次元一般の、上級者向け最適化
| minimize_scalar | minimize | |
|---|---|---|
| 対象 | 1変数のみ | 多変数(1変数も可) |
| 主な用途 | 教育・検証・1D推定 | 高次元モデル |
| 主手法 | Brent法(黄金分割+補間) | 勾配法・準Newton等 |
| 導関数 | 不要 | methodにより必要 |
| 初期値 | 不要 | 必須 |
| 発散リスク | ほぼない | method依存であり得る |
安定性・安全性
-
minimize_scalar(bounded)- 区間内に必ず収まる
- 初期値依存なし
- 単純・再現性が高い
-
minimize- 初期値で結果が変わる
- 局所解に依存
- 制約はmethod依存
使い分けのルールとしては、
1変数なら迷わず
minimize_scalar(bounded)
2変数以上になったらminimizeを検討
典型的な誤用
❌ 1次元問題に minimize を使う → 不必要に不安定・複雑・危険
まとめると、
-
minimize_scalarは「1次元最適化で使う」 -
minimizeは「多次元最適化の選択肢」
この記事は、minimize_scalar の話になります。
2. 数学:bounded は「区間制約付きBrent法」
2.1 解きたい問題
bounded が解くのは、制約付き1次元最小化:
\min_{x\in[a,b]} f(x)
導関数が使えなくてもよい(関数値評価だけで進む)のが強い。
2.2 Brent法の思想(速い+安全)
Brent法は基本的に次を混ぜる:
- 黄金分割探索(必ず収束、堅牢)
- 逆放物線補間(当たると速いが外れると危険)
そして
うまくいきそうなら加速(補間)
危なければ必ず収束する道(黄金分割)に戻る
という設計になっている。
method="bounded" は提案点を常に $[a,b]$ に制限するので、
物理的に不正な領域へ飛びにくい。
黄金比については下記を参照ください。
3. 物理:最小化は「安定点を探す」行為
物理では安定状態が
\min_x E(x)
として表されることが多い(ポテンシャル最小、自由エネルギー最小など)。
最小化アルゴリズムは、ある意味
「系が自然に落ち着く場所」を数値的に再現する道具
である。
4. 統計:最尤推定は「NLL最小化」
最尤推定(MLE)は
\hat{\theta} = \arg\max_\theta \mathcal{L}(\theta)
\quad\Longleftrightarrow\quad
\arg\min_\theta \mathrm{NLL}(\theta)
であり、実務では 負の対数尤度 (Negative Log Likelihood; NLL) を最小化する。
このとき「誤差」をどう出すかが重要になる。
5. 誤差評価の2つの流儀:ΔNLL と 曲率(ラプラス近似)
5.1 ΔNLL=0.5 ≈ 1σ(Wilks / ラプラス近似の範囲)
正則条件+十分なサンプル数のもとで、最尤点近傍では
\Delta\mathrm{NLL}(x)
=\mathrm{NLL}(x)-\mathrm{NLL}(\hat{x})
\approx \frac{1}{2}\left(\frac{x-\hat{x}}{\sigma}\right)^2
となり
\Delta\mathrm{NLL}=0.5 \ \Longleftrightarrow\ |x-\hat{x}|\approx\sigma
つまり ΔNLL=0.5 の左右交点が概ね ±1σに対応する
(プロファイル尤度の考え方。詳細はAppendixを参照)。
5.2 曲率(ラプラス近似)σ:局所二次近似の「理想下限」
一方で、最尤点の局所曲率から
\sigma_{\text{Laplace}}=\frac{1}{\sqrt{\partial^2\mathrm{NLL}/\partial x^2}}
も得られる。これは Fisher情報・ラプラス近似に対応する。
ただしこれは
- 最尤点の一点の局所情報
- 二次近似が効くことを暗黙に仮定
- モデルが正しく、十分大きなサンプルという理想条件
のもとで、しばしば 誤差の下限(楽観側、誤差を小さめに評価) になりやすい。
6. 実務テンプレ(最終版コード):最小化+検証+±1σ+可視化
以下が、本記事の結論となる 「論文品質の1次元最適化テンプレ」 である。
設計方針は次の通り:
-
最小性チェックは warning
→ 数値誤差・評価ノイズ・丸めで“完全な極小”にならないことがあるため、即死させない -
曲率チェックは原則 raise(救済付き)
→ 曲率が正でないなら σ の定義が崩れる(誤差推定が破綻する) -
±1σは ΔNLL=0.5 の左右交点を brentq で求める
→ 形状(非対称性・尾の重さ)を反映できる - さらに 曲率σも同じ図に重ねて描く
→ ラプラス近似がどれだけ楽観的かを「見える化」する
サンプルコードが解いている数理問題
このサンプルコードは、観測データ ${k_i}_{i=1}^N$ が 同一のポアソン分布
k_i \sim \mathrm{Poisson}(\lambda)
に従うと仮定し、その 平均パラメータ $\lambda$ を
最尤推定(Maximum Likelihood Estimation; MLE) により求めるものである。
尤度の定義
ポアソン分布の確率質量関数は下記である。
P(k \mid \lambda) = \frac{e^{-\lambda}\lambda^k}{k!}
独立な観測が $N$個あるとき、尤度関数はその積として
\mathcal{L}(\lambda) = \prod_{i=1}^{N}
\frac{e^{-\lambda}\lambda^{k_i}}{k_i!}
と定義される。
なぜ対数を取るのか(対数尤度)
尤度は積の形をしており、データ数が多いと数値的に扱いづらい。
そこで単調変換である 対数 を取り、和の形に変換する:
\log \mathcal{L}(\lambda)
=
\sum_{i=1}^{N}
\left(
-\lambda
+
k_i \log \lambda
-
\log k_i!
\right)
このうち $\log k_i!$ は $\lambda$ に依存しないため、
最適化(最大化・最小化)には影響しない。
最小化問題としての書き換え(NLL)
最尤推定は
\hat{\lambda}
= \arg\max_\lambda \log \mathcal{L}(\lambda)
で定義されるが、数値計算では等価な形として
負の対数尤度(Negative Log-Likelihood; NLL)
\mathrm{NLL}(\lambda)
= -\log \mathcal{L}(\lambda) = N\lambda -\left(\sum_{i=1}^{N} k_i\right)\log\lambda
\quad
(+\ \text{定数})
を 最小化 する問題として解いている。
\boxed{
\hat{\lambda}
= \arg\min_{\lambda>0}
\mathrm{NLL}(\lambda)
}
これが、サンプルコードで minimize_scalar(method="bounded") に渡している
目的関数の正体である。
コード上でやっていること(数式対応)
-
poisson_nll(lambda, counts)
→ 上式の $\mathrm{NLL}(\lambda)$ をそのまま数値関数として実装 -
minimize_scalar(..., method="bounded")
→ $\lambda>0$ という物理的制約のもとで
$\mathrm{NLL}(\lambda)$ を最小化 -
得られた最小点 $\hat{\lambda}$
→ 最尤推定値(MLE)
補足:解析解との関係
この単純な場合、解析的にも
\hat{\lambda}
= \frac{1}{N}\sum_{i=1}^{N} k_i
(=サンプル平均)となることがわかる。
本コードはこの既知の結果を 数値最適化で再現しつつ、
- 尤度曲線の形状確認
- 誤差(ΔNLL = 0.5 による 1σ)評価
- 将来、解析解が存在しないモデルへの拡張
を見据えた 汎用テンプレートとして用意したものです。
※以下のコードは google colab でも動作できます。
import numpy as np
import warnings
import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar, root_scalar
def _bracket_root_on_side(g, x0, side, bounds, *, growth=1.8, max_steps=60):
"""
g(x)=0 の根を x0 の片側(left/right)で brentq できるように符号変化区間を見つける。
- g は連続を仮定(ΔNLL-0.5 なら通常OK)
- bounds=(a,b) の範囲内で探索
"""
a, b = float(bounds[0]), float(bounds[1])
if side == "left":
x1 = x0
y1 = g(x1)
if y1 == 0:
return (x1, x1)
x2 = x0
step = (x0 - a) / 50.0 if x0 > a else 1.0
for _ in range(max_steps):
x2 = max(a, x2 - step)
y2 = g(x2)
if np.sign(y1) != np.sign(y2):
return (x2, x1)
step *= growth
return None
elif side == "right":
x1 = x0
y1 = g(x1)
if y1 == 0:
return (x1, x1)
x2 = x0
step = (b - x0) / 50.0 if x0 < b else 1.0
for _ in range(max_steps):
x2 = min(b, x2 + step)
y2 = g(x2)
if np.sign(y1) != np.sign(y2):
return (x1, x2)
step *= growth
return None
else:
raise ValueError("side must be 'left' or 'right'")
def minimize_scalar_with_checks_plot_and_1sigma(
f,
bounds,
*,
args=(),
xatol=1e-10,
eps_factor=10.0,
curvature_retry_factors=(1.0, 3.0, 10.0),
dNLL_target=0.5,
out_png="near_minimum.png",
):
"""
1) minimize_scalar(method="bounded")
2) 最小性チェック(warnで継続)
3) 曲率チェック(正でなければraise。eps救済あり)
4) ΔNLL可視化(PNG保存)
5) ΔNLL=dNLL_target の左右交点(≈±1σ)を brentq で求め、図に縦線を描く
"""
# 1) 最適化
res = minimize_scalar(
f,
bounds=bounds,
args=args,
method="bounded",
options={"xatol": xatol, "maxiter": 500},
)
if not res.success:
raise RuntimeError(f"Optimization failed: {res.message}")
x = float(res.x)
f0 = float(res.fun)
# 2) 近傍チェック用 eps(x≈0で潰れない)
eps0 = eps_factor * xatol * max(1.0, abs(x))
fL = float(f(x - eps0, *args))
fR = float(f(x + eps0, *args))
tol_f = 1e-12 * max(1.0, abs(f0))
is_min_like = (fL >= f0 - tol_f) and (fR >= f0 - tol_f)
if not is_min_like:
warnings.warn(
"Local-minimum check is suspicious (might be numerical noise or multimodality). "
"Proceeding anyway. "
f"(x={x:.6g}, eps={eps0:.3g}, fL={fL:.6g}, f0={f0:.6g}, fR={fR:.6g})",
RuntimeWarning,
)
# 3) 曲率(>0)チェック:救済付き
curvature = None
used_eps = None
for fac in curvature_retry_factors:
eps = eps0 * fac
fLm = float(f(x - eps, *args))
fRp = float(f(x + eps, *args))
curv = (fLm - 2.0 * f0 + fRp) / (eps * eps)
if np.isfinite(curv) and curv > 0:
curvature = curv
used_eps = eps
break
if curvature is None:
raise RuntimeError(
"Curvature check failed: could not obtain positive curvature with retries. "
f"(x={x:.6g}, eps0={eps0:.3g}, tried={curvature_retry_factors})"
)
sigma_laplace = 1.0 / np.sqrt(curvature)
# 4) ΔNLLの定義(一般fでも可)
def dF(xx: float) -> float:
return float(f(xx, *args) - f0)
# 5) ΔNLL=dNLL_target の左右交点を brentq で求める
def g(xx: float) -> float:
return dF(xx) - dNLL_target
# 左側
brL = _bracket_root_on_side(g, x, "left", bounds)
x_lo = None
if brL is not None:
if brL[0] == brL[1]:
x_lo = brL[0]
else:
solL = root_scalar(g, bracket=brL, method="brentq")
if solL.converged:
x_lo = float(solL.root)
# 右側
brR = _bracket_root_on_side(g, x, "right", bounds)
x_hi = None
if brR is not None:
if brR[0] == brR[1]:
x_hi = brR[0]
else:
solR = root_scalar(g, bracket=brR, method="brentq")
if solR.converged:
x_hi = float(solR.root)
if (x_lo is None) or (x_hi is None):
warnings.warn(
f"Could not find both Δf={dNLL_target} crossings by brentq within bounds. "
f"(x_lo={x_lo}, x_hi={x_hi}). "
"This can happen for shallow curves, non-unimodal shapes, or too-tight bounds.",
RuntimeWarning,
)
# 6) 可視化範囲の決め方:brent交点が取れたらそれを優先
a, b = float(bounds[0]), float(bounds[1])
if (x_lo is not None) and (x_hi is not None):
plot_lo = max(a, x_lo - 0.6 * (x_hi - x_lo))
plot_hi = min(b, x_hi + 0.6 * (x_hi - x_lo))
else:
plot_lo = max(a, x - 5.0 * sigma_laplace)
plot_hi = min(b, x + 5.0 * sigma_laplace)
xs = np.linspace(plot_lo, plot_hi, 500)
ys = np.array([dF(xx) for xx in xs], dtype=float)
plt.figure(figsize=(6.5, 4.2))
plt.plot(xs, ys, label="Δf(x)=f(x)-f(x̂)")
plt.axvline(x, color="k", linestyle="--", label="x̂ (MLE/opt)")
plt.axhline(dNLL_target, color="gray", linestyle=":", label=f"ΔNLL={dNLL_target:g} (~1σ)")
# ±1σ(ΔNLL交点)を描く
if x_lo is not None:
plt.axvline(x_lo, linestyle="--", label="x̂-1σ (ΔNLL=0.5)")
if x_hi is not None:
plt.axvline(x_hi, linestyle="--", label="x̂+1σ (ΔNLL=0.5)")
# 参考:曲率からのラプラス近似σも可視化(欲しければ)
plt.axvline(x - sigma_laplace, linestyle=":", label="x̂-σ (curvature)")
plt.axvline(x + sigma_laplace, linestyle=":", label="x̂+σ (curvature)")
plt.xlabel("x")
plt.ylabel("ΔNLL (or Δobjective)")
plt.title("Near-optimum shape and 1σ interval (ΔNLL method)")
plt.legend(fontsize=9)
plt.tight_layout()
plt.savefig(out_png, dpi=150)
plt.show()
plt.close()
sigma_from_dNLL = None
if (x_lo is not None) and (x_hi is not None):
sigma_from_dNLL = 0.5 * (x_hi - x_lo)
return {
"x": x,
"fun": f0,
"sigma_laplace": sigma_laplace,
"curvature": curvature,
"curvature_eps": used_eps,
"x_1sigma_lo": x_lo,
"x_1sigma_hi": x_hi,
"sigma_from_dNLL": sigma_from_dNLL,
"dNLL_target": dNLL_target,
"result": res,
"png": out_png,
}
def poisson_nll(lam: float, counts: np.ndarray) -> float:
if lam <= 0:
return np.inf
n = counts.size
s = counts.sum()
return n * lam - s * np.log(lam)
rng = np.random.default_rng(0)
lam_true = 7.5
counts = rng.poisson(lam_true, size=200)
out = minimize_scalar_with_checks_plot_and_1sigma(
poisson_nll,
bounds=(1e-12, 50.0),
args=(counts,),
xatol=1e-12,
out_png="poisson_mle.png",
)
print("lambda_hat =", out["x"])
print("sigma (Laplace/curvature) =", out["sigma_laplace"])
print("1σ interval (ΔNLL=0.5) =", (out["x_1sigma_lo"], out["x_1sigma_hi"]))
print("saved figure =", out["png"])
7. 実行結果の読み方:図の3種類の線が意味するもの
lambda_hat = 7.485000089786349
sigma (Laplace/curvature) = 0.00011099584479981405
1σ interval (ΔNLL=0.5) = (7.293207643367668, 7.680125665224874)
saved figure = poisson_mle.png
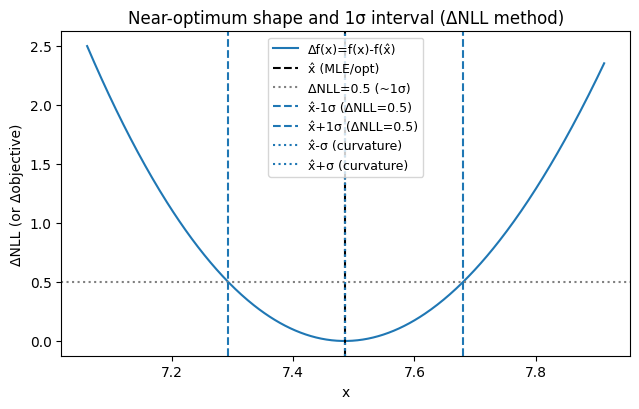
出力される poisson_mle.png(上図)には、最低限次が描かれる:
- 黒破線:最尤点 $\hat{x}$
- 灰点線(水平):$\Delta\mathrm{NLL}=0.5$(概ね 1σ)
- 黒破線(左右):$\Delta\mathrm{NLL}=0.5$ の左右交点(プロファイル尤度の ±1σ)
- 青点線(左右):曲率(ラプラス近似)から得た $\hat{x}\pm\sigma_{\text{Laplace}}$
ここで重要なのは「2つの誤差が一致しているか?」である。
- ほぼ一致
→ NLL が十分に二次的(正規近似が妥当)、誤差評価は堅い - 曲率σが明らかに小さい
→ ラプラス近似が楽観的(誤差過小評価の疑い) - 左右が非対称
→ 対称誤差バー(±σ)でまとめるのは不適切(非対称誤差を使うべき)
8. なぜ「曲率(ラプラス近似)誤差」は過小評価になりやすいのか
ここが本記事の核心である。
8.1 曲率σは「最尤点の一点」しか見ていない
曲率σは
- $x=\hat{x}$ の近傍での
- 二次近似の係数
だけから決まる。
しかし実際のNLLは
- 少し離れたところで平坦化する
- 境界で歪む(例:$\lambda>0$)
- 尾が重い(非ガウス)
- 有限サンプルでギザつく
などが普通に起こる。
その場合、
最尤点の“局所曲率”は鋭く見えても、
±1σ相当の領域は意外と広い
ということが起こる。
8.2 曲率σは「下限」に近い量(Cramér–Rao的)
ラプラス近似や Fisher 情報由来のσは、統計学的には
- 正則性
- モデル正しさ
- 漸近(大標本)
のもとでの理想的な推定誤差であり、しばしば
「これ以上小さくはならない」側の値(楽観側)
になる。
したがって、曲率σを 無検証で論文に出すと、
- 系統誤差やモデル不確かさが吸収されず
- 誤差が不自然に小さく見え
- “検出”や“整合”が過剰に強く見える
という事故の温床になる。
8.3 だから図に「両方」描く
本記事の実装が意図しているのは単純である:
ΔNLL(プロファイル)と曲率σを同じ図に並べ、
誤差過小評価が起きていないかを“目で検査”する
これができるだけで、解析や論文の信頼性は一段上がる。
9. まとめ
minimize_scalar(bounded) を「論文品質」にするチェックリスト
-
minimize_scalar(bounded)は堅牢な1次元最適化だが、success=True は最小性や妥当性を保証しない -
実務では最低限:
- 近傍最小性チェック(疑わしければ warn)
- 曲率>0チェック(誤差推定が目的ならほぼ必須)
- ΔNLL可視化(形状確認)
-
誤差評価は ΔNLL(プロファイル)を主にし、曲率σは比較用に使う
-
2つが乖離するなら、曲率σによる誤差過小評価を疑うべき
Appendix : 補足事項
ΔNLL=0.5 と 1σ、Wilks・ラプラス近似、境界条件、曲率σの限界
A.1 記号と前提
以降、1次元パラメータ $x$ の最尤推定を考える。尤度を $\mathcal{L}(x)$、負の対数尤度を
\mathrm{NLL}(x) \equiv -\log \mathcal{L}(x)
と定義する。最尤推定値は
\hat{x} = \arg\min_x \mathrm{NLL}(x)
である。本Appendixで使う代表的近似は次の2つ:
- ラプラス近似(局所二次近似):$\hat{x}$ の近傍で $\mathrm{NLL}(x)$ を2次で近似
- Wilks の定理:尤度比統計量が漸近的に $\chi^2$ に従う(正則性と大標本が必要)
A.2 ラプラス近似:なぜ ΔNLL が二次形になるのか
最尤点 $\hat{x}$ の近傍で、$\mathrm{NLL}$ をテイラー展開する:
\mathrm{NLL}(x)
= \mathrm{NLL}(\hat{x}) + \frac{1}{2}~\mathrm{NLL}''(\hat{x}) (x-\hat{x})^2
+ O\left((x-\hat{x})^3\right).
最尤点では $\mathrm{NLL}'(\hat{x})=0$ なので一次項が消える。
よって
\Delta \mathrm{NLL}(x)
\equiv \mathrm{NLL}(x)-\mathrm{NLL}(\hat{x})
\approx \frac{1}{2}~\mathrm{NLL}''(\hat{x}) (x-\hat{x})^2.
ここで
\sigma_{\text{Laplace}}
\equiv \frac{1}{\sqrt{\mathrm{NLL}''(\hat{x})}}
と置くと
\Delta \mathrm{NLL}(x)
\approx \frac{1}{2}\left(\frac{x-\hat{x}}{\sigma_{\text{Laplace}}}\right)^2.
したがって
\Delta \mathrm{NLL}=0.5
\quad\Longleftrightarrow\quad
|x-\hat{x}| \approx \sigma_{\text{Laplace}}.
ここまでが「ΔNLL=0.5 が概ね 1σ」という経験則の中身である。
注意:これはあくまで 局所二次近似が十分成り立つ範囲での話であり、尾部・非対称性・境界に弱い。
A.3 Wilks の定理:ΔNLL=0.5 が 68%CI に対応する背景
Wilks の定理は、正則条件のもとで
-2\log\frac{\mathcal{L}(x)}{\mathcal{L}(\hat{x})}
\ \xrightarrow[n\to\infty]{d}\ \chi^2_{k}
($k$ は検定する自由度)を述べる。1次元では $k=1$。
ここで
-2\log\frac{\mathcal{L}(x)}{\mathcal{L}(\hat{x})}
= 2\left(\mathrm{NLL}(x)-\mathrm{NLL}(\hat{x})\right)
= 2\Delta \mathrm{NLL}(x).
したがって、漸近的に
2\Delta \mathrm{NLL}(x)\sim\chi^2_1.
$\chi^2_1$ の 68%点はおおよそ 1 に対応するため(厳密には 68.27%…の点)、
2\Delta \mathrm{NLL}=1
\quad\Longleftrightarrow\quad
\Delta \mathrm{NLL}=0.5
が 約 68%信頼区間(≈1σ) になる、という理屈である。
重要:Wilks は「正則条件」と「大標本」を必要とする。境界・離散性・弱い同定・小標本では崩れる。
A.4 「曲率σ(ラプラス近似)」と「ΔNLL交点σ(プロファイル)」の違い
A.4.1 曲率σ(ラプラス近似)
\sigma_{\text{Laplace}}=\frac{1}{\sqrt{\mathrm{NLL}''(\hat{x})}}
は、最尤点の 1点の局所情報しか使わない。
よって、
- 非線形性(3次以上)
- 非対称性
- 尾の重さ
- 境界の影響
を反映しにくい。
A.4.2 ΔNLL交点(プロファイル尤度)
\Delta \mathrm{NLL}(x)=0.5
の左右交点 (x_-), (x_+) を求め、
\sigma_- = \hat{x}-x_-,\quad
\sigma_+ = x_+-\hat{x}
として 非対称誤差を自然に扱える。
さらに、二次近似が壊れる場合も「壊れた形のまま」反映されるため、実務上はこれが強い。
A.5 境界
(例:$\lambda>0)$があると何が壊れるか
ポアソン率 $\lambda$ は $\lambda>0$ が自然であり、多くの問題で「境界」が本質的に入る。
境界があると:
- $\hat{\lambda}$ が境界近くに張り付くことがある(暗い天体など)
- $\mathrm{NLL}$ の形が対称でなくなる
- Wilks の正則条件が破れやすい(パラメータ空間の内部でなく端点に最適点がある)
このとき、曲率σは特に危険で、
- 曲率は局所的に大きい(鋭く見える)
- しかし片側は境界で伸びない(区間が片側だけになる)
という形で 誤差が小さく見えがちである。
A.6 小標本・離散性での注意点(Poissonは特に)
Poissonは観測が離散で、暗い領域では
- $k_i=0,1,2$ が並ぶ
- NLL が滑らかな放物線に見えない
- “情報量”がそもそも不足する
ことがよく起きる。
このとき、
- Wilks の漸近論が効かない
- ΔNLL=0.5 が 68% と一致しない
- プロファイル区間が不連続に見えることもある
という状況があり得る。
実務上の対処としては:
- 図(ΔNLLカーブ)を必ず出す
- 区間分割スキャンで多峰性・平坦部を検出する
- 必要ならベイズ(事前分布)やブートストラップで頑健化する
が現実的である。
A.7 多峰性のとき:ΔNLL=0.5 が「別の谷」に飛ぶ問題
多峰性があると、
- そもそも $\hat{x}$ が局所最小
- ΔNLL=0.5 の交点探索が、別の谷を拾う
- 「1σ」という概念が1つの谷の局所概念に過ぎない
という問題が出る。
実務上の安全策
- まず区間分割で粗スキャンし、谷が複数あるかを確認
- “最小の谷”を選ぶだけでなく、「次点の谷との差」も記録
- 図に複数の谷が見えたら、誤差以前にモデル・同定性を議論する
A.8 なぜ曲率σは過小評価になりやすいのか(典型パターン)
曲率σが小さく出やすい典型例は次:
- 局所は鋭いが、少し離れると平坦(尾が重い・ロバスト損失)
- 境界の存在(片側が切られている)
- モデルミススペック(誤差モデルが甘い:PoissonなのにGaussian扱い等)
- フィッティングの自由度過多(実質的にデータが拘束していない方向がある)
- “条件付き”曲率をそのまま使う(他パラメータ固定での二次曲率など)
要するに、
曲率σは「理想下限」に近い
現実の不確かさはそれより大きくなる要因が多い
という構造がある。
A.9 実務の推奨:論文での誤差提示の作法
本記事のメッセージを実務ルールに落とすなら:
- 主:$\Delta\mathrm{NLL}=0.5$ の交点(プロファイル尤度)で ±1σ(非対称なら非対称で)
- 副:曲率σ(ラプラス近似)を比較として併記(図に重ねるのが強い)
- 必須:ΔNLLカーブを可視化し、形状(非対称・平坦・多峰性)を確認する
-
注意:境界・小標本・多峰性では「1σ」という言葉自体を慎重に使う
(“profile-likelihood interval” と言ってしまうのも手)
A.10(おまけ)コード側の改善余地:非対称誤差を明示する
本体コードでは sigma_from_dNLL を半幅として返しているが、論文向けには
\sigma_-=\hat{x}-x_-,\quad \sigma_+=x_+-\hat{x}
をそのまま報告するのがより誠実である。
(必要なら return に sigma_minus, sigma_plus を追加するだけでよい。)
まとめ
数値最適化は、「計算機が勝手に答えを出してくれるテクニック」と思われがちですが、
限られた関数評価の中で、どこまで“確信を持って”最小点に近づけるか
という、極めて人間的な設計判断の積み重ねと言えるでしょう。
minimize_scalar(bounded) は、
- 放物線近似で「速く賭け」
- 黄金分割で「安全に戻る」
という、失敗を前提にした現実的な戦略を取っている。
最尤推定でも同様に重要なのは、「最小値が出たか」ではなく、
- その近傍がどれくらい鋭いか
- その鋭さに対して数値精度が十分か
- そもそも他に谷がないと言い切れるか
を自分の言葉で説明できるかどうかでしょう。
最適化結果を“信じる”ためには、
途中の風景(尤度曲線)を一度は自分の目で見ることが何よりの近道。