立教大学 Advent Calendar 2025

はじめてのアドベントカレンダー Advent Calendar 2025

@yamadasuzaku(Shinya Yamada)in

立教大学

2025年のノーベル物理学賞と宇宙観測とのつながりージョセフソン効果から巨視的量子トンネル（MQT）へ

Last updated at 2025-12-24Posted at 2025-12-03

はじめに

宇宙の高精度観測は、量子デバイスの進展とともに大きく進化してきました。しかし、宇宙を観る技術の基盤には、固体物理や量子力学の理解が不可欠です。

2025年のノーベル物理学賞は、巨視的量子トンネル（MQT） の実証と、その電気回路におけるエネルギー準位の量子化の発見に対して授与されました。一見すると「量子デバイス」や「固体物理」の領域の話に思えますが、その本質は“ミクロな現象がマクロな性能を決定する”という、現代の宇宙観測とも深くつながる物理です。1960年代にジョセフソンが示した「量子位相がマクロに現れる」という発見から、1980年代の MQT 実験、そして2025年のノーベル賞に至る流れは、TES をはじめとする量子センシング技術や高精度スペクトル観測がなぜ可能なのかを理解する上で極めて重要な歴史でもあります。

本記事では、ジョセフソン効果 → 巨視的量子トンネル → 量子準位の観測 → 宇宙観測技術への接続という流れを、宇宙天文を学ぶ学生でも読みやすい形で説明してみます。

マクロな量子現象への挑戦

まず、ジョセフソン効果と巨視的量子トンネル現象の違いについて、1960年代の発見から 2025 年ノーベル物理学賞に至るまで、簡単に整理しておきます。

1960年代、ジョセフソン効果（Josephson effect）の発見によって、量子力学的な波動関数の位相という「ミクロ」な物理量が、「マクロ」なスケールで観測できることが示されました（例：Josephson effect - Wikipedia、Brian D. Josephson – NobelPrize.org）。

一方、2025年のノーベル物理学賞は、巨視的量子トンネル現象（MQT: Macroscopic Quantum Tunneling）の発見(代表例がジョセフソン接合を用いた電気回路（rf-SQUID や電流バイアス接合）)と、その系でのエネルギー準位の量子化の実証に対して授与されました（Nobel Prize in Physics 2025 – NobelPrize.org、Popular information）。

本記事では下記を念頭に、1960年代から2025年に至る流れを整理します。

ジョセフソン効果（直流・交流）の基礎と、そこに現れる量子干渉
1980年代に行われた MQT 実験
- 「傾斜した洗濯板型」ポテンシャルによる模型
- 量子化されたエネルギー準位
「量子干渉」と「量子状態の観測」という視点から両者を比較し、その代表例としてジョセフソン接合の位相差が量子力学的自由度として振る舞うことを量子準位とトンネル脱出率の精密測定で直接検証した2025 年ノーベル賞研究の意義を考えます。

(専門家の方向け) 日本物理学会からの解説記事

日本物理学会誌に掲載された、蔡兆申先生の以下の解説記事をご覧ください。

また、日本物理学会誌に掲載された以下の記事もご覧ください。

これらの記事をいきなり読むのは敷居が高いかもしれませんので、以下ではなるべく簡単に解説してみたいと思います。

ノーベル物理学賞から科学史を読み解くときの注意点

科学の進展は通常、「理論・発見」→「検証」→「実用化・改良」という長いプロセスを経る。しかし、ノーベル賞は，多段階の研究プロセスの中で，特定の「象徴的成果」だけを切り出して顕彰することもある。そのため、

ノーベル賞は科学を映す“鏡”ではなく、一部分を強調する“レンズ”である。

という見方もできます。この観点は踏まえた上で、2025 年ノーベル物理学賞（巨視的量子トンネル） を、1960 年代のジョセフソン効果の発見から考えてみましょう。

量子トンネル研究の歴史の概観

1960 年代は、固体中での量子トンネル現象が一気に明確化し、一気に実験的に確立した時代

■ 1. Giaever（1960–61）：超伝導ギャップの“直接観測”に成功

Ivar Giaever は Al/AlOx/Nb 型など，当時実際に用いられていた種々の SIS 接合（典型例として Al の自然酸化膜をバリアとするもの）を用いて、超伝導体の状態密度（DOS）に現れる エネルギーギャップ Δ を I–V 曲線として直接観測した。

BCS 理論の重要な予言である

ギャップ Δ の存在
DOS(=Density of States;状態密度)特異点（コヒーレンスピーク）

を、実験として初めて明示した功績である。

DOS (= Density of States; 状態密度) の補足

DOS は “エネルギーごとの座席数” を表す普遍的な概念ですが、何を座らせるか（電子・原子・中性子など）と、どのような椅子の配置か（結晶格子・量子井戸・超伝導ギャップなど）によって、その計算方法や意味づけは物理系ごとに大きく異なります。
超伝導体の BCS 理論では、特にフェルミ準位近傍の電子状態の DOS が重要で、ペアリング相互作用によって DOS がギャップ構造やコヒーレンスピークを持つ形へと変形されます。
したがって物性物理において「状態密度」と聞いたときには、“どの粒子を扱っていて、どの相互作用を主役にしているか” というその系の"舞台設定"を考えながら意味を解釈することが大切です。

● 当時のバリア形成：主流は “自然酸化 (native oxidation)”

Al を蒸着し、空気に晒すだけでできる自然酸化膜（Al₂O₃）
- 厚さ：1–2 nm 程度
- 制御性：低い（均質性と再現性は限定的）
しかし偶然にも良質なバリアとなり、トンネル分光が成立した。

(勝手な想像) 実験屋の感覚としては「Al を蒸着して放置すれば酸化されてバリアができる」という、今日から見るとかなり素朴なアイディアだったのでしょう。(当時はまだコンピューターもないので、相当な苦労があったのでしょう。)

■ 2. Josephson（1962）：位相が“電流源になる”と理論予言

BCS 理論が導入する巨視的波動関数 $\Psi = |\Psi| e^{i\phi}$ の位相差 Δφ が電流を生む と予言した。

予言内容：

直流ジョセフソン効果（DCJ）：電圧なしで電流が流れる
交流ジョセフソン効果（ACJ）：電圧 V に対し $f = 2eV/h$ の振動電流が流れる

ミクロな量子位相が、マクロな量（電流）に直接現れるという理論であった。

（→ 1973 年ノーベル物理学賞：Giaever, Esaki, Josephson）

Josephson は「Cooper対の位相が電流になる」という理論予言

Giaever は「BCSギャップという超伝導の中身を“直接測った”」という実験的基盤の確立

江崎玲於奈は「固体における電子トンネルの一般原理を実証」

Josephson effect - Wikipedia
R. Gross, Applied Superconductivity – Josephson Effects（PDF）

■ 3. Anderson & Rowell（1963）：DC ジョセフソン効果を実験で検証

フィリップ・アンダーソンと John M. Rowell は、Al/AlOx/S 接合を改良し、
電圧ゼロでも電流が流れるという DC ジョセフソン効果を実験的に確認した。

これにより、

量子位相の実在性
Cooper 対がトンネル障壁を貫通する現象
$I = I_c \sin\phi$ の位相依存性

が明瞭に示され、Josephson 理論が実験的に裏付けられた。

(補足)1960年代には、2つのジョセフソン接合をリング状に配置した SQUID（超伝導量子干渉計） で磁束に対する臨界電流の振動（干渉縞）が観測され、ジョセフソン電流が波動関数の干渉に由来することが明瞭に示されました。

■ 4. Shapiro（1963）：AC ジョセフソン効果を検証（Shapiro ステップ）

RF（マイクロ波）照射下で、

I–V 曲線に量子化ステップが現れる（Shapiro ステップ）

という現象を観測。
そこから、

hf = 2eV

の関係式が実証され、ACジョセフソン効果が決定的になった。

（→ 後に 電圧標準（Josephson voltage standard） として国家標準へ発展）

■ 5. 現代への橋渡し：ジョセフソン接合と低温技術の進化

1970〜80年代には、

Nb/Al–AlOx/Nb の薄膜プロセスが確立
大量生産可能・低ノイズ・高安定な接合が登場

し、ジョセフソン接合は“巨視的量子系の実験舞台”として確立した。

希釈冷凍機の開発史

1960年代半ばに Leiden や Manchester など複数のグループが ³He–⁴He 希釈冷凍機の連続運転に成功し、ミリケルビン温度が実用化された。1970〜80年代には Oxford Instruments や Kölner Gruppe により 液体ヘリウムを用いる湿式（wet）希釈冷凍機が研究用途で普及し、固体物性・超伝導実験の標準装置となった。1990年代後半〜2000年代にはパルスチューブ冷凍機が急速に進歩し、これと組み合わせた 無冷媒（cryogen-free）型希釈冷凍機が 2000 年代半ばに実用化。2010年代以降は Bluefors や Leiden Cryogenics が高信頼化・大型化を進め、量子ビット、超伝導遷移端検出器(TES)など、低温物理の世界的スタンダードとなった。(cf., 100mK冷凍機としてはXRISM衛星などで使われてる断熱消磁冷凍機というのもあります。)

◇ 低温技術が実験の地平を拡張した

1960年代：まだ希釈冷凍機が一般的ではなく、減圧 He を用いた数 K 〜 1 K 程度の実験が主流
1980年代：希釈冷凍機により 100 mK 以下の安定した測定が可能に

→ これが、後の 巨視的量子トンネル（MQT） 研究を支える基盤の一つになったのでしょう。

■ 6. 2025 年ノーベル物理学賞：巨視的量子トンネルと量子準位の観測

ジョセフソン接合を“人工量子井戸”とみなすと、その中の マクロ自由度（位相差）が量子トンネルすることがある。希釈冷凍機・高度化した微細加工技術により、

量子トンネルの直接観測
量子化されたエネルギー準位の同定

がついに実現した。これは、

古典的なポテンシャル井戸に閉じ込められた“マクロ”変数が
“ミクロの量子力学そのもの”に従う

ことを示す象徴的な成果であり、その意義が評価され、2025 年ノーベル物理学賞として結実した。

2025 年ノーベル物理学賞の背景概説

ジョセフソン接合における巨視的量子トンネル（MQT）や準位量子化を理解する上で欠かせないのが、「位相差 φ が、あるポテンシャル面に沿って運動する粒子としてふるまう」 という視点です。これは突然出てくるアイデアではなく、接合を回路として扱ったときの実効的な力学方程式から自動的に現れます。

🚿 洗濯板ポテンシャル（Washboard Potential）の簡単な説明

ジョセフソン接合とRCSJ モデル

RCSJ モデル（Resistively and Capacitively Shunted Junction）は、Josephson 接合の位相差を力学変数とみなす有名なモデルで、以下の電流関係式から始まります：

I = I_c \sin\phi + \frac{\hbar C}{2e}\ddot{\phi} + \frac{\hbar}{2eR}\dot{\phi}

ここで

$I_c$：臨界電流
$\phi$：超伝導位相差
$C, R$：接合の容量・抵抗

第二項は「慣性」、第三項は「粘性（抵抗）」に相当します。この方程式は、傾いた周期ポテンシャル中の粒子の運動方程式と同一の形になります。

座標を φ ではなく磁束 $\Phi = (\Phi_0/2\pi)\phi$ とみなし、
そのときの「質量」を $m = C (\hbar/2e)^2$ と定義する
ことが多いです。ノーベル賞の解説記事
ここでは便宜的に『質量』$\propto C$ とみなす（座標を φ に取るか Φ に取るかで係数は変わる）」

以下では、Josephson 接合の並列回路（3 要素） → RCSJ モデル → 位相の運動方程式 → ポテンシャル → 洗濯板ポテンシャルまでを一気通貫でまとめて説明してみます。

🧩 Josephson 接合 → RCSJ → 運動方程式 → ポテンシャル → 洗濯板ポテンシャル

1. Josephson 接合は“3 要素の並列回路”で表現される

実際の Josephson 接合は、以下の 3 要素が 並列に接続された回路として等価に表すことができる：

純粋な Josephson 素子（非線形素子）：
```
I_J = I_c \sin\phi
```
抵抗 $R$（トンネル障壁を通らないリーク電流）：
```
I_R = \frac{V}{R}
```
容量 $C$（電極間の電荷蓄積）：
```
I_C = C \frac{dV}{dt}
```

外部から流れる電流 (I) は三つの並列経路に分配されるため：

I = I_J + I_R + I_C

2. Josephson の AC 関係式で電圧を位相に置き換える

抵抗と容量の電流に含まれる“電圧 $V$”は、Josephson の第二式（AC Josephson 効果）で位相差と結び付けることができる：

V = \frac{\hbar}{2e}\dot{\phi}.

これを上式へ代入すると：

抵抗電流

I_R = \frac{\hbar}{2eR}\dot{\phi}

容量電流

I_C = \frac{\hbar C}{2e}\ddot{\phi}

3. RCSJ の運動方程式（位相 φ の力学方程式）

三つの電流を足し合わせると、位相 φ の運動を支配する方程式が得られる：

\boxed{
I = I_c \sin\phi

+ \frac{\hbar}{2eR}\dot{\phi}
+ \frac{\hbar C}{2e}\ddot{\phi}
  }

これは

質量：$\frac{\hbar C}{2e}$
摩擦：$\frac{\hbar}{2eR}$
非線形ばね：$I_c\sin\phi$
外力：$I$

をもつ一自由度の力学系：

m\ddot\phi + \eta \dot\phi + F(\phi) = I

に完全に対応する。

4. 復元力からポテンシャルを構成する

復元力は

F(\phi) = -I_c \sin \phi.

力学では

F = -\frac{dU}{d\phi}

なので、積分して

U_J(\phi) = -E_J \cos\phi,

E_J = \frac{\hbar I_c}{2e}.

これが 純粋なジョセフソン接合の位置エネルギー（コサイン井戸）。

5. 電流バイアス（外力）から傾きが加わる

外から流す直流電流 $I$ は一定の外力に対応し、
それに対応するポテンシャルは

U_I(\phi) = -\frac{\hbar}{2e} I \phi.

これは位置と比例する単調増加関数で、
コサインカーブの全体を一定の角度で傾ける効果を持つ。

6. ポテンシャルの完成形（洗濯板ポテンシャル）

純粋な Josephson の位置エネルギーと外力の項を足すと：

\boxed{
U(\phi)
= -E_J \cos \phi - \frac{\hbar}{2e} I~\phi
  }

これは、

コサインの周期的な凹凸（洗濯板の“板の溝”）
バイアス電流による傾き（洗濯板を斜めに立てかけた状態）

を合わせた形であり、

\text{“Washboard potential”（洗濯板ポテンシャル）}

と呼ばれる。

(ここでは '復元力' として Josephson 項 $-E_J\cos\phi$ だけを見る)

Washboard potential の導出の物理イメージのまとめ

並列回路で Josephson + R + C をモデル化する
電圧 V を位相 φ の時間変化に変換する（AC Josephson 効果）
すると I–V 回路式が 位相 φ の運動方程式になる
位相 φ に働く力を積分すると 位置エネルギー U(φ) が出る
そのエネルギーが 周期的で傾いた“洗濯板”の形になる
井戸に閉じ込められる or 井戸を越える → 電圧の有無、MQT が決まる

→ RCSJ の式から洗濯板ポテンシャルが自然に導かれ、Josephson 接合のダイナミクスが説明できる。

RCSJ モデルの補足説明

RCSJ（Resistively and Capacitively Shunted Junction）モデルは、1960 年代後半に Ivanchenko & Zil’berman、Stewart、McCumber らによって整えられた、ジョセフソン接合の標準的なダイナミクス記述です。彼らは、実際の接合は純粋な Josephson トンネル電流だけでなく、漏れ電流を担う抵抗 $R$ と、接合電極間に蓄積される電荷の慣性を担う容量 $C$ を必然的に併せ持つことを明確に示した。これにより位相差 $\phi$ の運動は、慣性$C$、粘性$R$、周期ポテンシャル（Josephson エネルギー）を持つ“粒子の運動”と数学的に完全に等価になり、一つの方程式でプラズマ振動、ヒステリシス、スイッチング、巨視的量子トンネル（MQT）といった幅広い現象を統一的に説明できるようになった。

素朴な疑問は「こんな単純な等価回路で本当に現実の接合を表せるのか？」という点でしょう。しかし、より複雑に見える物理（準粒子損失、誘電緩和、環境ノイズなど）は、結局すべて追加的な抵抗・容量・ノイズ源へと還元でき、RCSJ の基礎構造を損なわない。むしろ RCSJ は、どんなジョセフソン接合でも必ず存在する 3 つの普遍的力学成分——ばね（Josephson エネルギー）、ダンパー$R$、質量$C$ ——を抽出した“最小限でありながら一般性を失わない”モデルであり、この 3 項を落とすと基本的な挙動を記述できなくなる。だからこそ、RCSJ は半世紀以上にわたり超伝導デバイスの基盤理論として機能しているのでしょう。

特に注意すべき点は、Josephson 電流 $I_s = I_c \sin\phi$ がしばしば「非線形ばね」と呼ばれる理由である。単振動の解 $x(t)=A\sin(\omega t)$ が正弦波になると、力 $F(t)$ も正弦波的に見えるために「ばねが正弦で応答している」と誤解されがちだが、これは 時間的にたまたま正弦波が現れているだけで、線形ばねの本質は $F=-kx$（変位に比例すること）にある。すなわち、線形性とは「力と変位の比例関係」を指しており、時間波形の形とは本質的に無関係である。

これに対して Josephson 接合では、力に対応する項

F(\phi) = -E_J \sin\phi

が 変位 $\phi$ に比例せず、最大値を持ち、周期的に反転するという、根本的な非線形性を備えている。したがって位相が大きくなるにつれて線形近似から急速に逸脱し、これは洗濯板ポテンシャル・束縛井戸の量子化・MQT・位相量子ビットなど、Josephson 接合固有の多彩な物理現象の源泉となる。「$\sin\phi$ をテイラー展開すると高次項が出るから非線形」という説明も形式的には正しいが、より重要なのは “力が変位に比例しない”という質的な違いであり、これが Josephson 力が「非線形ばね」と呼ばれるゆえんです。

🌊 洗濯板ポテンシャルが意味するもの

● 「φ（位相）は粒子の位置」のように動く

φ がポテンシャル谷に閉じ込められていれば「超伝導（電圧ゼロ）状態」。
谷から抜け出して滑り落ちると φ が連続的に増加し「有限電圧」が現れます。

● バイアス電流 I を増やすと井戸が浅くなる

小電流 → 深い谷 → φ は量子井戸に閉じ込められる
大電流 → 傾きが増す → φ が脱出しやすくなる → 超伝導破壊

● MQT（Macroscopic Quantum Tunneling）が起きる意味

井戸が有限の深さを持つため、
位相 φ が量子トンネルで井戸から脱出する
（＝巨視的量子トンネル）が起こります。

φ のトンネルは

巨視的自由度
多数の Cooper ペアに対応する量子変数が量子トンネルすることを意味するため、“巨視的量子現象” となります。

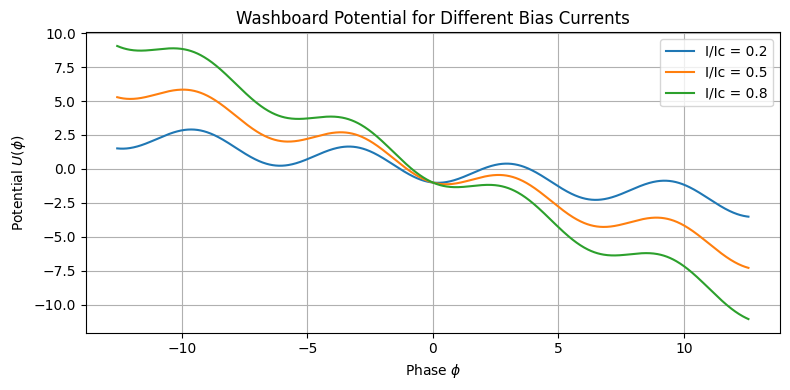
📈 洗濯板ポテンシャルを matplotlib でプロットするコード例

以下はほぼどの環境でも実行可能な Python スクリプトです。デフォルトでは電流 $I = 0.5I_c$ としています。

Google Colab の実行例も置いてます。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
Ic = 1.0               # critical current (arbitrary units)
Ej = 1.0               # Josephson energy scale
phi = np.linspace(-4*np.pi, 4*np.pi, 1000)  # phase range

# Bias currents to compare
current_list = [0.2*Ic, 0.5*Ic, 0.8*Ic]
colors = ['tab:blue', 'tab:orange', 'tab:green']

plt.figure(figsize=(8,4))

for I, col in zip(current_list, colors):
    # Washboard potential
    U = -Ej * np.cos(phi) - (I/Ic) * Ej * phi
    plt.plot(phi, U, color=col, label=f'I/Ic = {I/Ic:.1f}')

plt.xlabel(r'Phase $\phi$')
plt.ylabel(r'Potential $U(\phi)$')
plt.title('Washboard Potential for Different Bias Currents')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

● この図の意味すること

cos の周期構造が見える
電流があるので右下がりの傾斜
谷が有限の深さ → MQT のトンネル障壁

電流を変えると井戸が浅くなり、$ I \to I_c $ で井戸が消失して滑り落ち状態になる様子も確認できます。

この「洗濯板ポテンシャル」の解説は、例えば以下にまとまっています。

NobelPrize.org, Scientific background 2025（PDF 内で washboard potential の図が出てきます）

1980年代の実験：MQT の観測とエネルギー準位の量子化

1980年代初頭、複数の研究グループが巨視的量子トンネル効果（MQT）　の実験的検証に着手しました。

典型的な流れは、ノーベル委員会の解説や John Clarke によるレビューに詳しくまとめられています：

J. Clarke, Quantum Mechanics of a Macroscopic Variable: The Phase Difference of a Josephson Junction, Science 239, 992 (1988).（Science link）

典型的な実験手法：スイッチング電流の統計

1980 年代初頭に、Voss & Webb らによる rf-SQUID での MQT 観測など、早い段階で量子トンネルを示唆する実験がすでに行われていた（ただしノイズやパラメータ評価の不確かさが大きかった）。

ジョセフソン接合を電流バイアスして、

バイアス電流をゆっくり増加させる
ある電流値で、接合がゼロ電圧状態 → 有限電圧状態にジャンプ（井戸から脱出）
この「スイッチング電流」を多数回測定し、その統計分布を調べる

温度を下げていくと：

高温：
- 熱ゆらぎによる「熱活性化脱出」が支配的
温度を下げていくと：
- 脱出電流（平均スイッチング電流）が大きくなる
- あるクロスオーバー温度以下で、脱出確率が温度に依存しない飽和が現れる

この温度非依存な脱出は、

「熱ではなく量子トンネルによって位相が井戸から脱出している」

可能性を強く示唆します。
ただし、低温での飽和は外部ノイズでも生じうるため、当時の研究者たちは高周波ノイズフィルタや環境遮断を徹底し、量子トンネルであることを慎重に検証しました。

バークレーグループによる実験

カリフォルニア大学バークレー校の John Clarke, Michel H. Devoret, John M. Martinis のグループによる一連の実験が、以前の先駆的実験を踏まえつつ，最も説得力のある定量的証拠を与えた

代表的論文：

M. H. Devoret, J. M. Martinis, J. Clarke,
Measurement of Macroscopic Quantum Tunneling out of the Zero-Voltage State of a Current-Biased Josephson Junction, Phys. Rev. Lett. 55, 1908 (1985).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.55.1908
J. M. Martinis, M. H. Devoret, J. Clarke,
Energy-Level Quantization in the Zero-Voltage State of a Current-Biased Josephson Junction, Phys. Rev. Lett. 55, 1543 (1985).（APS link）

彼らは：

極低温（ミリケルビン領域）
徹底した遮音・遮蔽・フィルタリング

という環境でジョセフソン接合を駆動し、共鳴活性化法を用いて系のパラメータを高精度に決定しました。

プラズマ振動の共鳴測定

微弱なマイクロ波を接合に印加
井戸内で位相が小振動する「プラズマ振動（プラズマ周波数 $\omega_p$）」を共鳴的に励起
その共鳴条件から：
- プラズマ周波数 $\omega_p$
- 減衰パラメータ
  を独立に決定

その上で、

既知パラメータを用いて 量子トンネルの理論脱出率 を計算
実測した脱出率と比較

すると、

十分低温での脱出率が、量子トンネル理論と定量的に一致する

ことが示され、巨視的量子トンネルの存在が否定しがたい形で確立されました。

量子エネルギー準位の直接観測

さらに、同じグループは井戸内の量子エネルギー準位の直接観測にも成功しました。

接合をゼロ電圧状態のまま保つ
弱いマイクロ波を照射し、その周波数を掃引
特定の周波数で、接合が井戸から脱出しやすくなる「共鳴」が現れる

これは、

マイクロ波エネルギー $\hbar\omega$ が井戸内のエネルギー準位差に一致
そのときだけ脱出確率が増大

していることを意味します。

このエネルギー準位量子化の観測は、先ほどの PRL 論文に詳述されています：

J. M. Martinis, M. H. Devoret, J. Clarke,
Energy-Level Quantization in the Zero-Voltage State of a Current-Biased Josephson Junction, Phys. Rev. Lett. 55, 1543 (1985).（APS link）

古典的な視点では、井戸内の小振動は単一周波数（プラズマ振動数 $\omega_p$）のみを持ちます。
しかし量子力学的には、井戸内には複数の離散準位が存在し、非調和ポテンシャルによりさまざまな遷移が可能になります。

複数の離散エネルギーレベルが検出されたことは、「この超伝導素子が古典ではなく量子力学に従っている」ことの、極めて強い証拠です。

直感的には：

井戸内のエネルギーは量子化されており、
低い準位ほど井戸に長く捕まり、
高い準位ほどトンネル脱出しやすい

という、量子力学的ポテンシャル井戸の教科書的な絵が、マクロな電気回路でそのまま再現された、ということになります。

「量子干渉」と「量子状態の観測」とは？

ジョセフソン接合では、同じ「位相差」という自由度が、実験条件と観測方法によって まったく異なる“量子現象の顔” を見せます。

1960年代：ジョセフソン効果（量子干渉の観測）
1980年代以降：MQT と準位量子化（量子状態の観測）

という二つの領域を、物理概念の違いが明瞭になるよう整理してみます。

1. ジョセフソン効果：連続位相による“巨視的量子干渉”の観測

ジョセフソン効果では、二つの超伝導体の巨視的波動関数

\Psi_1 = |\Psi_1| e^{i\phi_1}, \quad \Psi_2 = |\Psi_2| e^{i\phi_2}

の位相差

\phi = \phi_1 - \phi_2

がトンネル電流を支配します。

● 量子干渉としての本質

電流は
```
I = I_c \sin\phi
```
のように 連続変数としての位相に滑らかに依存する。
SQUID の干渉縞（磁束の周期性）は、二重スリット干渉になぞらえられるほど典型的な“量子干渉”の現れ。

● ここで観測されている量は？

観測しているのは 位相が連続的に変わることによる干渉効果。
位相が「量子力学的自由度」であることは含意されているが、
その内部に 離散エネルギー準位があるかどうかまでは見えてこない。

● 歴史的背景

ジョセフソン効果の発見当初（1960年代）は、位相差を「巨視的な位相因子」ととらえ、非線形インダクタ×トンネル素子として半古典的に扱うことも一般的だった。
この段階では、位相の「量子状態としての構造」にはまだ踏み込んでいない。

2. MQT と準位量子化：位相が“離散準位をもつ量子座標”であることの直接証拠

1980年代になると、微細加工技術・低温技術（希釈冷凍機）・ノイズ遮断技術の進展により、ジョセフソン接合の位相差そのものを量子力学的座標として扱い、その内部構造（固有準位）を直接測定できるようになった。

● 実験で明らかになったこと

井戸内の離散的エネルギー準位
- マイクロ波分光により、基底状態と励起状態のエネルギー差を直接測定。
位相粒子の量子トンネル（MQT）
- 電流バイアス下で井戸からの脱出率を測り、
  温度依存性（熱活性化 vs 量子トンネル）で区別。

特に 1985 年の Martinis–Devoret–Clarke (PRL) の一連の実験は：

パラメータ $R, C, I_c$ を独立に測定
プラズマ振動の共鳴周波数を精密に決定
脱出率が 量子トンネル理論とパラメータフリーで一致

という“教科書レベルの量子井戸”を、手のひらに乗るチップ上で実現したことを示しました。

● 観測している量は？

離散的な固有状態そのもの
それらの 量子遷移（マイクロ波励起）
井戸からの 量子トンネル（MQT）

これは「人工原子の分光」と全く同じ構造であり、位相が「量子ビットの座標」として適用可能であることを示す決定的証拠になった。

3. 二つの量子性の比較：何がどれだけ“深く”見えているか？

観測内容	ジョセフソン効果	MQT & 準位量子化
位相の扱い	連続変数としての干渉効果	離散エネルギー準位を持つ量子座標
実験で見える性質	干渉・周期構造・波動性	固有準位・遷移・トンネル・粒子性
測定手法	SQUID、干渉縞	スイッチング統計、マイクロ波分光
得られる知見	「マクロな量子干渉」	「マクロな量子状態そのもの」

どちらも「巨視的系が量子力学に従う」ことを示すが、MQT 実験の方が位相の量子力学的本質に“深く”踏み込んでいるといえる。

2025 年ノーベル物理学賞の意義：位相は“量子変数”であることの最終的な実証

2025 年ノーベル物理学賞は、

“in an electric circuit” における macroscopic quantum tunnelling と energy quantisation の発見

に対して授与された。

ここで強調されているのは、

対象は「ジョセフソン接合に限らない」と書かれているが、
実質的には ジョセフソン接合の位相 が
（1）量子トンネルし、（2）量子準位を持つことの実証

が中心である。

1. 位相は“古典的パラメータ”ではなく“量子自由度”である

1985 年の実験群は、

離散準位の観測
井戸深さとトンネル率の定量一致
マイクロ波誘起の遷移

などを通じて、

位相差 φ は、電子の位置やスピンと同様に、
明確な量子力学的自由度である

ことを決定的に示した。

これは、ジョセフソン効果だけでは見えなかった“量子構造そのもの”であり、巨視的量子コヒーレンス（ノーベル物理学賞受賞者のLeggettらが提唱した）の実験的裏付けともなった。

2. 巨視的スケールでの量子性の実証

ジョセフソン接合は、10⁸〜10⁹ 個の Cooper 対からなる巨大な量子集合体にも関わらず、

量子準位の存在
量子トンネルするダイナミクス

を原子系と同じ理論で説明できる。

これは、「量子力学はミクロだけの理論である」という直感に対する最も明確な反例の一つとなった。

3. 量子技術（量子ビット）への決定的な橋渡し

位相 φ が

離散準位をもち
トンネルにより遷移し
マイクロ波で制御できる

以上、これは 人工原子（量子二準位系） そのものである。

事実、1990〜2000年代には Martinis グループが位相量子ビットを開発し、コヒーレント制御を実証したことが現在の量子コンピュータ（超伝導量子ビット）の出発点になった。

まとめ

ジョセフソン接合は、超伝導体の位相差という自由度が離散準位と量子遷移を持つことから、“超伝導材で作られた人工原子（superconducting artificial atom）”とみなすことができる。

ジョセフソン効果は、位相干渉という“波の量子性” を示し、
MQT 実験は、離散準位とトンネルという“粒子の量子性” を示した。

この二つが統合されたことで、ジョセフソン接合は ミクロとマクロをつなぐ量子実験の代表格となり、
2025 年のノーベル物理学賞がその歴史的流れを明確に位置付けたといえるのでしょう。

宇宙観測とのつながり ― 「量子」はどこで生きているのか？

ここまで読んで 「で、これ宇宙と何の関係があるの？」 と思われた方に向けて、実験室で磨かれた量子物理が 現代の宇宙観測をどう支えているのか を短くまとめておきます。

1. SQUID と TES：X線・サブミリ波観測の心臓部

宇宙観測では、ジョセフソン電流そのものよりもSQUID（超伝導量子干渉計）を組み込んだ超伝導読み出し回路が圧倒的に重要です。

SQUID は超伝導ループ＋ジョセフソン接合で構成され、外部磁束に応じて臨界電流が Φ₀ (= h/2e) 周期で振動します。これによりフェムトテスラ級の磁場まで検出可能となります。
この高感度特性により、SQUID は TES や KID の読み出しアンプとして不可欠です。
TES（Transition-Edge Sensor）は、超伝導転移の急峻な抵抗変化を利用して単一光子のエネルギーを高精度で計測する検出器。
将来の宇宙X線観測ミッションでも、TES + SQUID 多重化読み出しが標準技術として採用されています。

2. CMB・重力波・ミリ波干渉計：量子限界ノイズへの挑戦

サブミリ波・ミリ波領域の観測では信号が極めて弱く、読み出しノイズを 量子限界近くまで抑える必要があります。

● ジョセフソン・パラメトリック増幅器（JPA/JPC）

ジョセフソン接合の非線形性を利用し、量子限界近い雑音性能でマイクロ波信号を増幅するデバイスです。

CMB 実験
重力波検出器の読み出し系
暗黒物質探索
超伝導量子ビット測定

などで重要な要素技術として研究が進んでいます。

ジョセフソンパラメトリック増幅器については、中村泰信先生のスライドなど。

● 大規模ミリ波アレイ：KID・TES

数千〜数万ピクセル級の検出器アレイでは、低雑音の読み出し技術が必須で、SQUID や JPA が中核的役割を果たします。

3. 宇宙衛星と実験室に共通する「極低温技術」

TES も MQT 実験も、動作温度は 数十 mK〜数百 mK と極低温です。そのため、以下の冷却技術が共通インフラになります。

希釈冷凍機（Dilution Refrigerator）
断熱消磁冷凍機（ADR）
パルスチューブ冷凍機

● 宇宙ミッションの例

XRISM/Resolve では、多段 ADR により50 mK 運用を安定維持できる設計が採用。
ASTRO-H（Hitomi）でも同様の多段冷却チェーンが採用されました。

● 地上量子実験との共通点

希釈冷凍機で 10 mK 程度まで冷却し、ジョセフソン接合の量子トンネル実験や量子ビット制御を実施。
多くの要素技術は宇宙用冷却システムと密接に対応しています。

4. 将来展望：人工原子としてのジョセフソン接合 → 次世代量子センサーへ

2025 年ノーベル物理学賞で強調された「ジョセフソン接合＝人工原子」という視点は、今後の宇宙観測技術にもつながります。

● 量子センサー化

ジョセフソン人工原子（トランスモンなど）を単一マイクロ波光子検出器として使う研究が進展。

14 GHz 帯の熱的マイクロ波光子を単一検出した例も報告されています。

● 量子変換器（マイクロ波 ⇔ 光子）

暗黒物質探索・重力波観測では超弱い相互作用を測る必要があり、マイクロ波信号を光に変換する量子トランスデューサが注目されています。

● 大規模アレイ読み出しへの応用

将来のミッションで必須となる数千〜数万ピクセル TES・KID アレイの量子限界読み出しに向けて、ジョセフソン系量子増幅器が鍵になります。

5. まとめ：ミクロの位相トンネルから、宇宙の高精度計測へ

1960年代に始まったジョセフソン効果と量子トンネル研究は、2025年ノーベル賞によって「人工原子の量子振る舞い」という形で大きな節目を迎えました。

しかし、その過程で磨かれた

ジョセフソン接合・SQUID
パラメトリック増幅器
希釈冷凍機・ADR
低雑音超伝導回路技術

といった技術群は、いまや 宇宙観測装置のインフラになっています。

たとえば将来のX線ミッションでは、TES マイクロカロリメータが1 eV 単位の精度でブラックホール周辺の線スペクトルを“聴き分ける” 時代も来るかもしれません。

そう考えると、ジョセフソン接合と MQT の物語は、単に固体物理の一エピソードではなく、“宇宙をどうやって高精度に測るか”という天文学の物語の一部でもある、とも捉えてみても良いでしょう。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

2025年のノーベル物理学賞と宇宙観測とのつながり ー ジョセフソン効果から巨視的量子トンネル（MQT）へ