誤差逆伝播法、何度勉強してもすぐ中身を忘れてしまうので、ゆるい図解で記憶することを目指します。
ほぼ自分用メモですが、せっかく頑張って作ったので、公開してみます。
ニューラルネットワークや誤差逆伝播とはなんぞやという点については解説をしませんので、
ニューラルネットワーク入門的な内容をお求めの方は、別の書籍や記事をご参照ください。
対象とするニューラルネットワーク
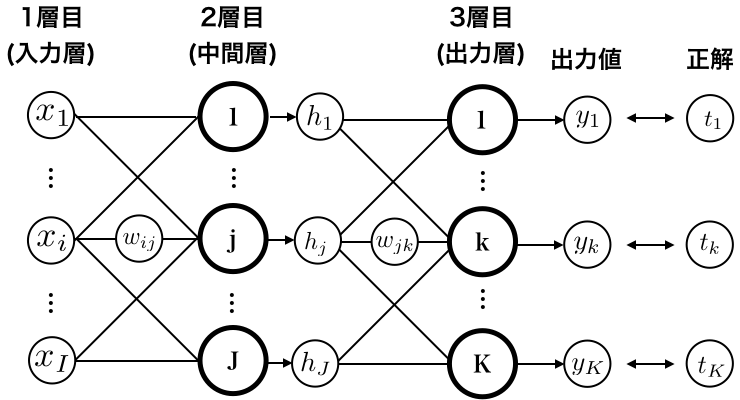
ここでは、スタンダードな3層MLPを対象にします。
$x_i$: 入力値
$w_{ij}$: 入力層と中間層の重み
$j$:中間層の$j$番目のノード
$h_j$: 中間層の出力
$w_{jk}$: 中間層と出力層の重み
$k$:中間層の$k$番目のノード
$y_{k}$: 出力値
$t_{k}$: 正解
順伝播
まずは、順伝播の処理を確認しておきます。
1層目(入力層)→2層目(中間層)
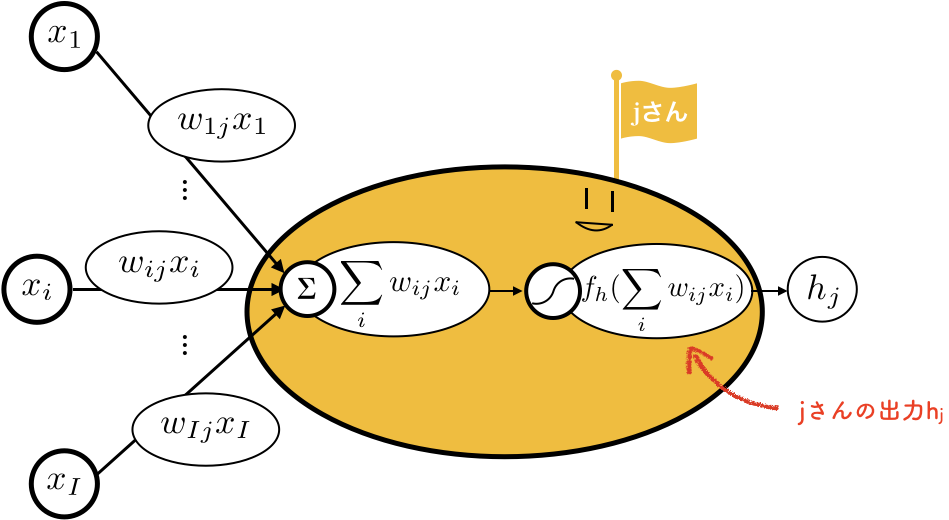
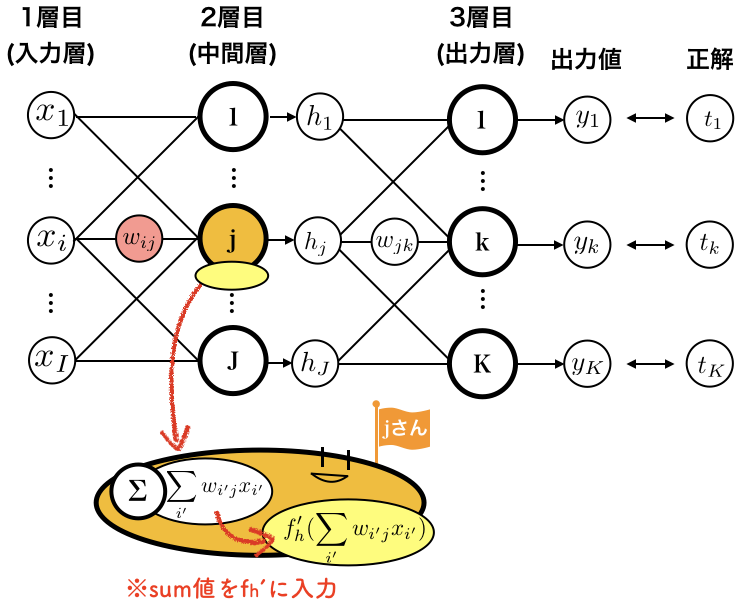
中間層のノード$j$に着目します。

順伝播では、この中でなにが起こるのか、拡大してみましょう。
中間層のノード、$j$さんです。ゆるい。
1層目の値に、重み$w_{ij}$がかけられて、$j$さんに集まってきます。
$j$さんはそれらを足し算($\sum$)します。
そして、活性化関数($f_h$)に入れます。
これが$j$さんの出力$h_j$となって出てきます。
※バイアス項も$\sum$の中に含まれている前提です
※u_{j}=$\sum_{i}w_{ij}x_i+b_j$, $z_{j}=f_h(\sum_{i} w_{ij}x_{i}+b_j)$のように別の記号で置き換える文献も多いですが、この記事では登場する記号を減らすため、あえてそのまま書きます
2層目(中間層)→3層目(出力層)
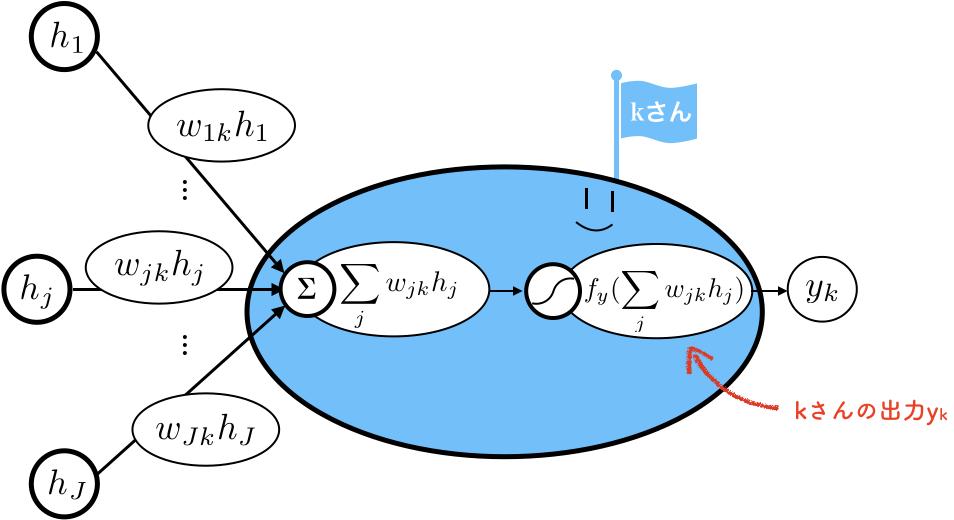
出力層のノード$k$に着目します。

これも、この中でなにが起こっているのか拡大してみましょう。
出力層のノード、$k$さんです。やはりゆるい。
前の層と同様に、2層目から入力された$h_j$に重み$w_{jk}$がかけられて、$k$さんに集まってきます。
$k$さんはそれらを足し算($\sum$)し、活性化関数($f_y$)をかけて、$y_k$を出力します。
逆伝播
逆伝播をざっくりおさらい
誤差逆伝播法では、まず、出力と正解の誤差を表す損失関数$E$を求めます。
$$ E = E(y_{1},y_{2}, ... , y_{k}, ... y_{K})$$
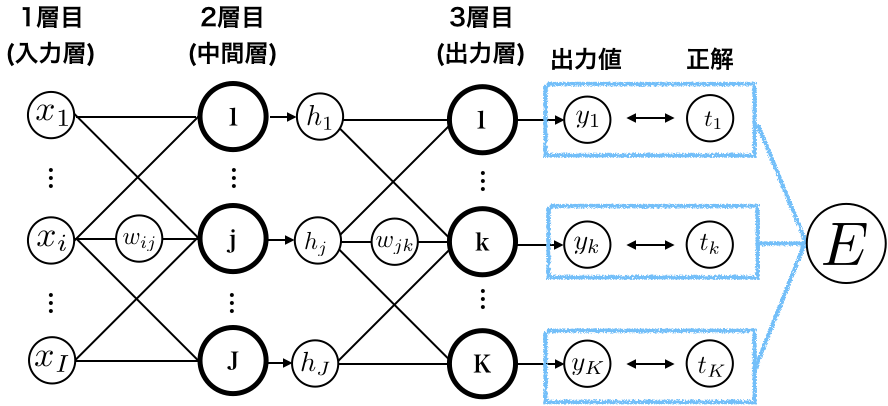
そして、誤差$E$が小さくなるように、ネットワークの重み$w$を学習していきます。
重み$w$は、勾配法をもちいて、以下の式で更新します。($\eta$は学習率)
$$ w \leftarrow w - \eta \frac{\partial E}{\partial w} $$
というわけで、ネットワーク上にいるすべての重み$w$を更新するためには、各$w$ごとに勾配$\frac{\partial E}{\partial w}$を計算してやる必要があります。
これから、そのようすを図解していきます。
2層目→3層目の重み更新
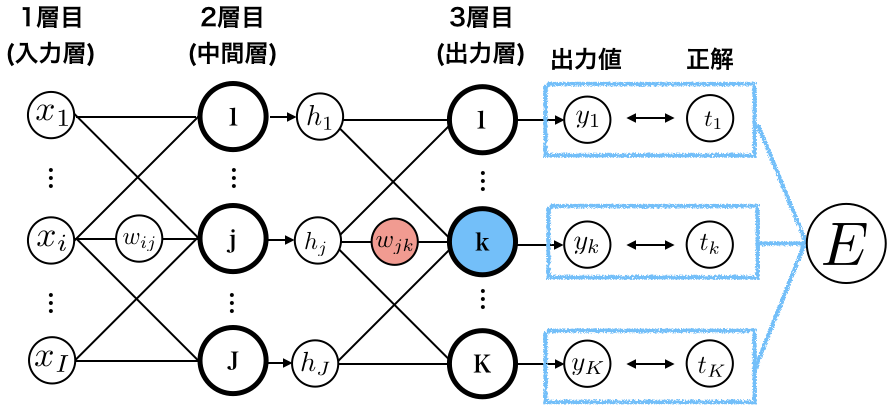
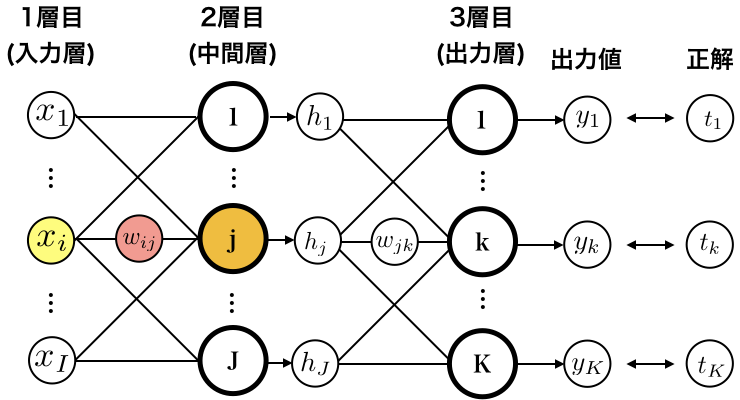
2層目→3層目の重みたち$w_{jk}$に対する$ \frac{\partial E}{\partial w_{jk}}$を求めます。
目につきやすいように、$w_{jk}$を赤色で塗りました。
まずは、数式の確認です。
\begin{eqnarray}
\frac{\partial E}{\partial w_{jk}} &=& \sum_{k'} \frac{\partial E}{\partial y_{k'}} \cdot \frac{\partial y_{k'}}{\partial w_{jk}} \\
&=& \frac{\partial E}{\partial y_{k}} \cdot \frac{\partial y_{k}}{\partial w_{jk}} \\
&=& \frac{\partial E}{\partial y_{k}} \cdot \frac{\partial f_{y}(\sum_{j’} w_{j’k}h_{j’})}{\partial w_{jk}} \\
&=& \frac{\partial E}{\partial y_{k}} \cdot f'_{y}(\sum_{j’} w_{j’k}h_{j’}) \cdot h_{j}
\end{eqnarray}
以下、数式展開の解説です。興味ない人や「わかってるよ!」って人は飛ばしていいです。
1行目の左辺→右辺では、微分の連鎖律(Chain Rule)を使っています。よーわからん場合はこちらの記事も参照。
2行目は、$\frac{\partial y_{k'}}{\partial w_{jk}}$が$k'\neq k$のとき0になることを使って、$k$の項だけ残しました。
3〜4行目は粛々と合成関数の微分をしています。外側の微分かける内側の微分、です。$w_{jk}$の$j$とごっちゃにならないよう、sumの添え字は $j'$を使っています。
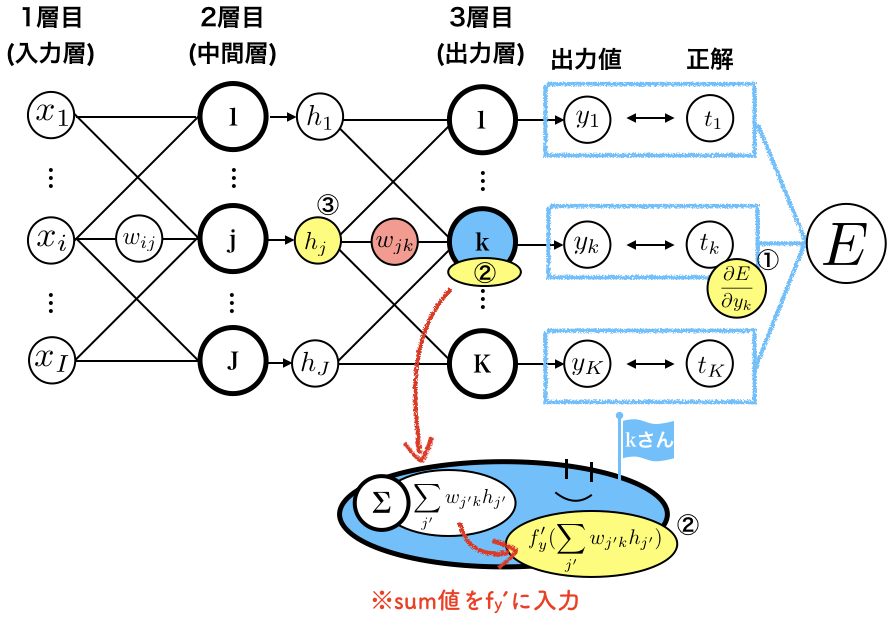
さてさて、最後の行は、$\frac{\partial E}{\partial y_{k}}$と、$f_y’(\sum_{j'} w_{j'k}h_{j'}))$と、$h _j$の、3つのかけ算になっていることがわかります。
ネットワーク上でいうと、
黄色い丸の3つの値、右から、
- $E$を$y_k$で微分した、$\frac{\partial E}{\partial y_{k}} $
- $k$さんのお腹の中にあるsum値を、関数$f_{y}'$に入力して得られる値、$f_{y}'(\sum_{j'} w_{j'k}h_{j'})$
- 一つ前の層からの入力値、$h_{j}$
の部分です。
この3点セットを使うと、$w_{jk}$の勾配$\frac{\partial E}{\partial w_{jk}}$が計算できます。
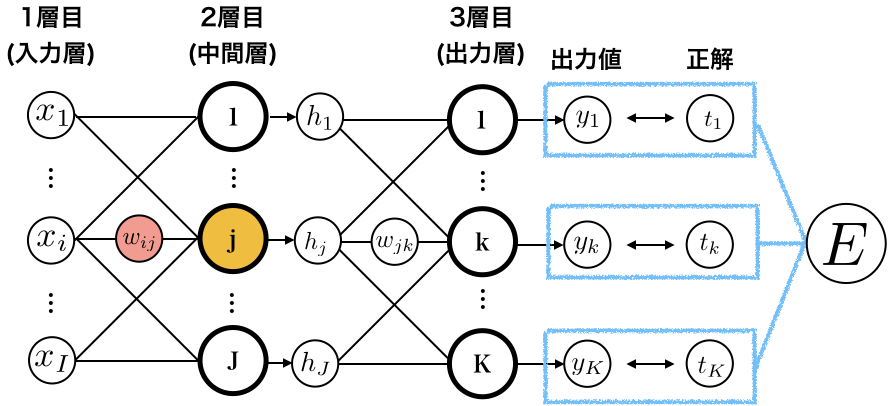
1層目→2層目の重み
お次は、1層目→2層目の重みたち$w_{ij}$を更新するために、$ \frac{\partial E}{\partial w_{ij}}$を求めます。
出力層から遠いので、ちょっと大変です。
まずは、数式の確認です。
\begin{eqnarray}
\frac{\partial E}{\partial w_{ij}} &=& \sum_{k} \frac{\partial E}{\partial y_{k}} \cdot \frac{\partial y_{k}}{\partial w_{ij}} \\
&=& \sum_{k} \frac{\partial E}{\partial y_{k}} \cdot \sum_{j'} \frac{\partial y_{k}}{\partial h_{j'}} \cdot \frac{\partial h_{j'}}{\partial w_{ij}} \\
&=& \sum_{k} \frac{\partial E}{\partial y_{k}} \cdot \frac{\partial y_{k}}{\partial h_{j}} \cdot \frac{\partial h_{j}}{\partial w_{ij}} \\
&=& \sum_{k} \frac{\partial E}{\partial y_{k}} \cdot f'_y( \sum _{j'} w_{j'k}h_{j'}) \cdot w_{jk} \cdot \frac{\partial h_{j}}{\partial w_{ij}} \\
&=& \sum_{k} \frac{\partial E}{\partial y_{k}} \cdot f'_y( \sum _{j'} w_{j'k}h_{j'}) \cdot w_{jk} \cdot f'_h(\sum_{i'} w_{i'j}x_{i'}) \cdot x_i
\end{eqnarray}
うわぁー。げんなりしますね。
以下は数式展開の解説ですが、げんなりした人は飛ばしてOKです。
1行目の左辺→右辺は、先ほどと同様に連鎖律を使っています。
2行目は、$\frac{\partial y_{k}}{\partial w_{ij}}$を、連鎖律を使ってさらに展開しています。ここで、$w_{ij}$の$j$とごっちゃにならないように、展開したときの添え字を$j’$にしています。
3行目は、$j’\neq j$のとき$\frac{\partial h_{j'}}{\partial w_{ij}}$が0になることを使って、$j$の項だけ残しました。
4行目は、$\frac{\partial y_{k}}{\partial h_{j}}$を展開してます。外側の微分×中身の微分、です。ここでも、$w_{ij}$の$j$とごっちゃにならないように、添え字に$j’$を使っています。
5行目は、$\frac{\partial h_{j}}{\partial w_{ij}}$を展開してます。外側の微分×中身の微分。こんどは、$w_{ij}$の$i$とごっちゃにならないように、添え字に$i’$を使っています。
さてさて、ここからは飛ばさないでください。
最後の式をよーく見ると、
$\sum_{k} \frac{\partial E}{\partial y_{k}} \cdot f_y'( \sum_{j'} w_{j'k}h_{j'}) \cdot w_{jk} $ と、 $f_h'(\sum_{i'} w_{i'j}x_{i'})$ と、 $x_i$の、かけ算になっていることがわかります。
なんだか複雑なので、分けて考えます。
はじめの長い項($\sum_{k} \frac{\partial E}{\partial y_{k}} \cdot f_y'( \sum_{j'} w_{j'k}h_{j'}) \cdot w_{jk} $)ですが、
$\frac{\partial E}{\partial y_{k}}$ と、 $f_y'(\sum_{j'} w_{j'k}h_{j'})$ と、$w_{jk}$をかけて、kについて足し上げたものになっています。
ネットワーク上で図解すると、
- $E$を$y_k$で微分した$\frac{\partial E}{\partial y_{k}} $
- $k$さんのお腹のsum値を$f_{y}'$に入力して得られる$f_{y}'(\sum_{j'} w_{j'k} h_{j'})$
- ノード$j$とつながっている重み$w_{jk}$
にあたります。
(1と2は2→3層目のときにも出てきましたね)
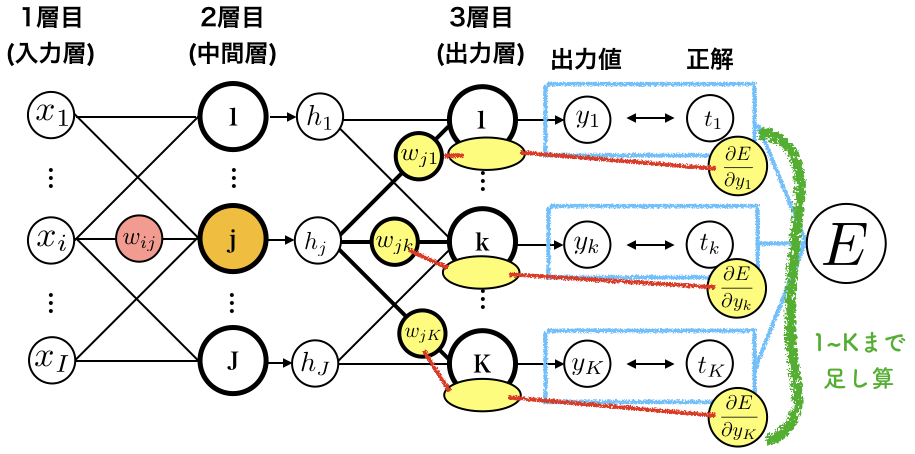
この3つをかけ算して、1〜Kまで足しあげると、はじめの長い項になります。
以下の図の、赤い線でつないだところをかけ算して、緑の線の範囲を足し算します。
はじめの長い項が何をしているのか、イメージがついてきました。
つぎの、$f_h’(\sum_{i'} w_{i'j}x_{i'})$は、$j$さんのお腹の中にあるsum値を$f_h’$に入力したものです。
最後の$x_i$は、入力値そのままですね。
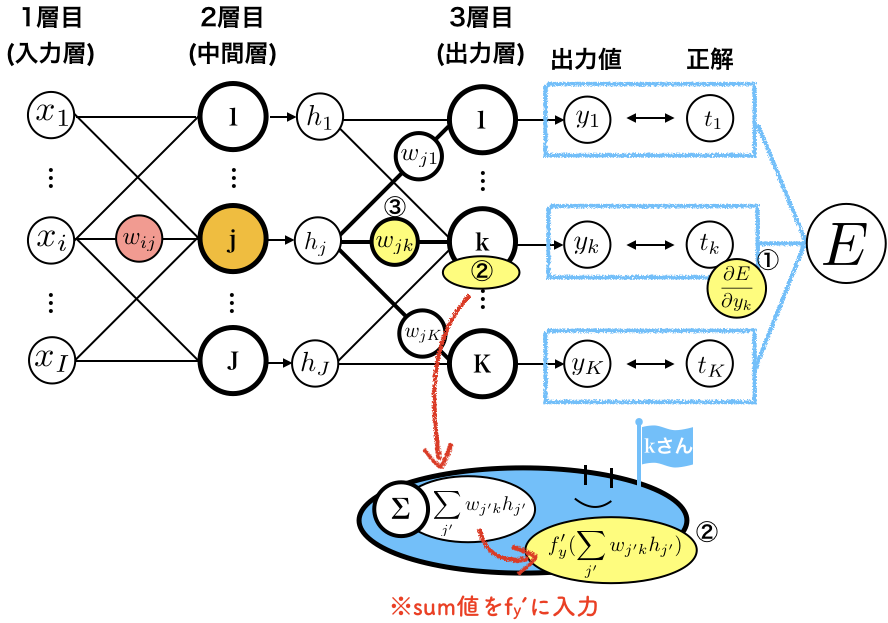
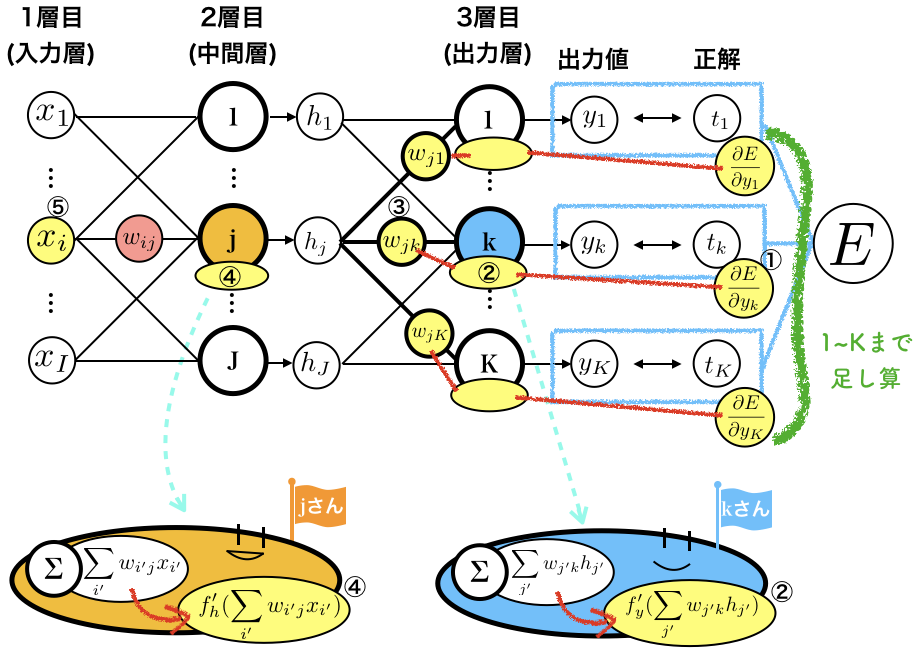
まとめると、$w_{ij}$の勾配$\frac{\partial E}{\partial w_{ij}}$を求めるときは、以下の図の黄色い部分の値を使います。
右から、
- $E$を$y_k$で微分した$\frac{\partial E}{\partial y_{k}} $
- $k$さんのお腹のsum値を$f_{y}'$に入力して得られる$f_{y}'(\sum_{j'} w_{j'k} h_{j'})$
- ノード$j$とつながっている重み$w_{jk}$
をかけ算して1〜Kまで足したもの、 - $j$さんのお腹の中で計算される$f_h’(\sum_{i'} w_{i'j}x_{i'}+b_j)$
- 入力、$x_i$
となります。
ごちゃごちゃ〜としていますが、
・前の層からの誤差(①×②)を重みづけ(③)して足したもの
・お腹の中のsum値をf’に入力したもの(④)
・一つ前の層からの入力値(⑤)
の3点セットで求まる、ということが見えるとよいと思います。
まとめ
誤差逆伝播法の勾配の更新式はネットワーク上のどこの値を使っているのか、
ゆるい絵とともに図解してみました。
実際の参考書では、前の層からの誤差がδで書かれていたりしますが、やってることは同じだと思います。
層が深くなっても、重みの更新式は、
前の層の誤差を足したもの、お腹の中、入力値、
の3点セットで計算できます。
なんとなく、理解の助けになれば幸いです。