はじめに
今年は機械学習の勉強をやり直すことにしました。
昔の記事に「Chainerで機械学習と戯れる: 2進法を学習できるか?」があり、タイトル名から勉強には良さそうだと思ってやってみました。
機械学習の習い事で論理演算(AND,OR,XOR)をなんとなく理解した後、そのイメージでこの記事のやっていることを理解しようとすると何をしているのか引っ掛かる部分がありました。
何をしているのか理解した後に今回の記事を書いています。
問題
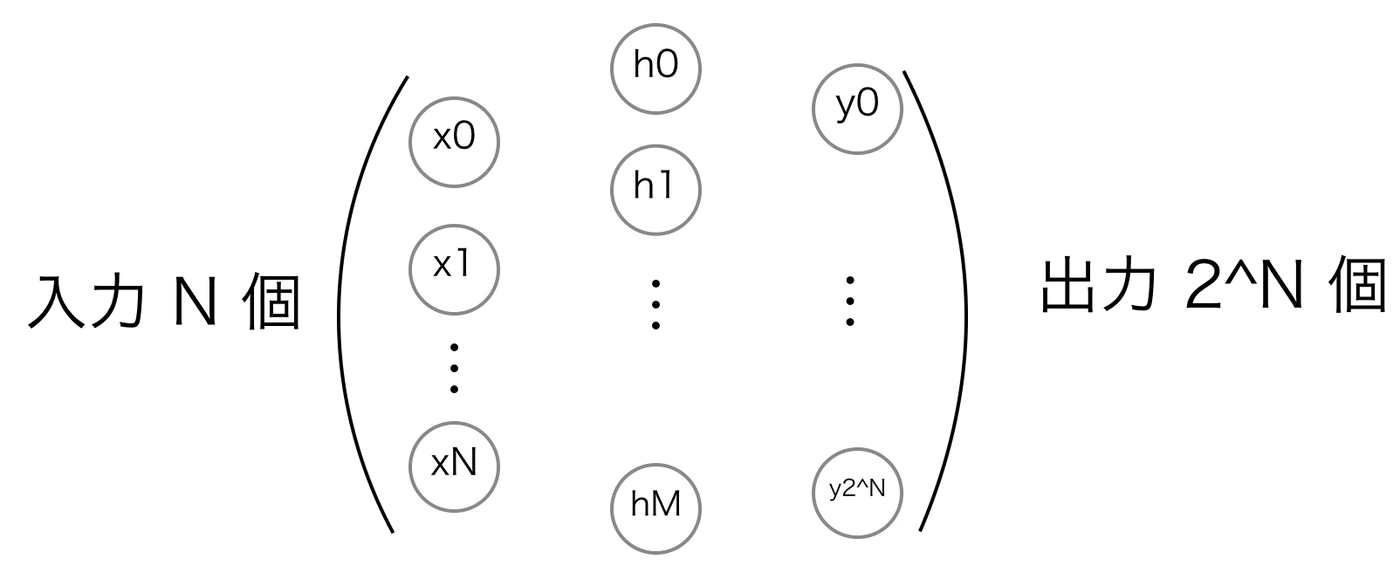
今回は N bit の入力を、対応する $2^N$個のどれかに出力するという問題を考えます。
中間の隠れ層は1層(H1)、もしくは、無しで試してみます。図にしてみるとこんな感じです。
不明な点
ソースコードのコメントには下記のように書かれていました。
「N bit の 2進数で表される $2^N$ 個の数字を $2^N$個のOutputのどれかを1にするということを学習させる。」
意味が分からず値を当てはめてみても、まだよく分かりませんでした。
4 bit の 2進数で表される 16 個の数字を 16個のOutputのどれかを1にするということを学習させる。
2 bit の 2進数で表される 4 個の数字を 4個のOutputのどれかを1にするということを学習させる。
入力の N bitは、論理演算(AND,OR,XOR)を学習した際にやっているので理解できたのですが、出力の数の意味が理解できなかったのです。論理演算のときは出力は1つでしたからね。
正解ラベルが4bitの時に0〜15の連番になっているのも、一体どういうことなんだろう?
まずはソースコードを実際に動かすことから始めてみました。
環境
元記事は2015年の記事で、出始めのChainerが使用されています。
確認する上で、Google Colaboratoryに最新のChainerをインストールした。
Chainerのインストール
Chainerを使用するのに、Google ColaboratoryをGPUインスタンスにする必要があります。
ランタイム - ランタイムのタイプを選択より、ハードウェアアクセラレータをGPUに変更し保存します。
Google Colaboratoryの無料GPU環境を使ってみた
!curl https://colab.chainer.org/install | sh -
% Total % Received % Xferd Average Speed Time Time Time Current
Dload Upload Total Spent Left Speed
100 1580 100 1580 0 0 15192 0 --:--:-- --:--:-- --:--:-- 15192
+ apt -y -q install cuda-libraries-dev-10-0
Reading package lists...
Building dependency tree...
Reading state information...
cuda-libraries-dev-10-0 is already the newest version (10.0.130-1).
0 upgraded, 0 newly installed, 0 to remove and 10 not upgraded.
+ pip install -q cupy-cuda100 chainer
|████████████████████████████████| 369.7MB 46kB/s
+ set +ex
Installation succeeded!
Chainerの確認
import chainer
chainer.print_runtime_info()
Platform: Linux-4.19.112+-x86_64-with-Ubuntu-18.04-bionic
Chainer: 7.4.0
ChainerX: Not Available
NumPy: 1.19.5
CuPy:
CuPy Version : 7.4.0
CUDA Root : /usr/local/cuda
CUDA Build Version : 10010
CUDA Driver Version : 11020
CUDA Runtime Version : 10010
cuBLAS Version : 10201
cuFFT Version : 10101
cuRAND Version : 10101
cuSOLVER Version : (10, 2, 0)
cuSPARSE Version : 10300
NVRTC Version : (10, 1)
cuDNN Build Version : 7605
cuDNN Version : 7605
NCCL Build Version : 2506
NCCL Runtime Version : 2506
iDeep: 2.0.0.post3
ソースコード
元記事のソースコードはこちら
https://github.com/mokemokechicken/PlayingChainer/blob/master/src/play1/binary.py
Chainerの最新バージョンで動作するように修正しています。
- python2 から python3 に変更
- import chainer.links as L を追加
- FunctionSet から Chain に変更
- F.Linear から L.Linear に変更
- model.collect_parameters() から model に変更
- optimizer.zero_grads() から model.cleargrads() に変更
- print は、print() に変更
- ファイルアクセスの fp は削除、print() に変更
仕組みを知るために、2bitのみで中間の隠れ層は無しにしています。
forward メソッドにて、精度 1.0の時に値を表示するようにしています。
"""
N bit の 2進数で表される 2**N 個の数字を 2**N個のOutputのどれかを1にするということを学習させる。
"""
import numpy as np
from chainer import cuda, Function, Chain, gradient_check, Variable, optimizers
import chainer.functions as F
import chainer.links as L
def forward(model, x_data, y_data):
x = Variable(x_data)
t = Variable(y_data)
if hasattr(model, "l2"):
h1 = model.l1(x)
y = model.l2(h1)
else:
y = model.l1(x)
loss = F.softmax_cross_entropy(y, t)
accuracy = F.accuracy(y, t)
if accuracy.data == 1:
print("x: %s\nt: %s\ny: %s" % (x, t, y))
return loss, accuracy
def generate_training_cases(n_bit):
x_data = []
t_data = []
output_len = 2**n_bit
for i in range(output_len):
x_data.append(list((int(x) for x in ("0"*n_bit + bin(i)[2:])[-n_bit:])))
t_data.append(i)
return np.array(x_data, dtype=np.float32), np.array(t_data, dtype=np.int32)
def main(n_bit, h1_size):
if h1_size > 0:
model = Chain(
l1=L.Linear(n_bit, h1_size),
l2=L.Linear(h1_size, 2**n_bit)
)
else:
model = Chain(
l1=L.Linear(n_bit, 2**n_bit)
)
optimizer = optimizers.SGD()
optimizer.setup(model)
x_data, t_data = generate_training_cases(n_bit)
for epoch in range(100000):
model.cleargrads()
loss, accuracy = forward(model, x_data, t_data)
loss.backward()
if epoch % 100 == 0:
print("epoch: %s, loss: %s, accuracy: %s" % (epoch, loss.data, accuracy.data))
if accuracy.data == 1:
break
optimizer.update()
print("epoch: %s, loss: %s, accuracy: %s" % (epoch, loss.data, accuracy.data))
return epoch, accuracy.data
if __name__ == '__main__':
for n_bit in range(2, 3):
# for h1_size in [0, n_bit, n_bit * 2, n_bit * 4, 2**n_bit]:
for h1_size in [0]:
epoch, accuracy = main(n_bit, h1_size)
print("%s\t%s\t%s\t%s\n" % (n_bit, h1_size, epoch, accuracy))
調査
仕組みを知るために、2bitのみで中間の隠れ層は無しにしました。
精度 1.0の時に変数の値を表示した結果となります。
※結果は実行するたびに 毎回epoch数が変わります。
epoch: 0, loss: 1.7298789, accuracy: 0.25
epoch: 100, loss: 1.5373461, accuracy: 0.0
epoch: 200, loss: 1.3871217, accuracy: 0.5
epoch: 300, loss: 1.2691685, accuracy: 0.5
epoch: 400, loss: 1.1733202, accuracy: 0.5
x: variable([[0. 0.]
[0. 1.]
[1. 0.]
[1. 1.]])
t: variable([0 1 2 3])
y: variable([[ 0.16063161 -0.1438682 -0.1438679 0.12710449]
[-0.17513631 0.34572977 -0.38719684 0.09932865]
[-0.38197905 -0.3428704 0.38396972 0.17577396]
[-0.717747 0.14672755 0.14064081 0.14799812]])
epoch: 449, loss: 1.132056, accuracy: 1.0
2 0 449 1.0
入力値のxは2進数の4つ、正解ラベルのtは0-3の連番までは理解できるとして、yの値はどういう数字なんだろう?
そこで、「softmax_cross_entropy(y, t)」の仕組みが分かれば何か見えてくるかも知れない。
softmax_cross_entropy(y, t)の手動計算
softmax_cross_entropyは、活性化関数Softmaxと損失関数Cross Entropyとの合成関数です。
検索してみると「[Softmax cross entropy誤差を手計算]
(https://s732714.hatenablog.com/entry/2019/06/01/200052)」という記事を見つけて、Excelで今回の値に当てはめてみました。
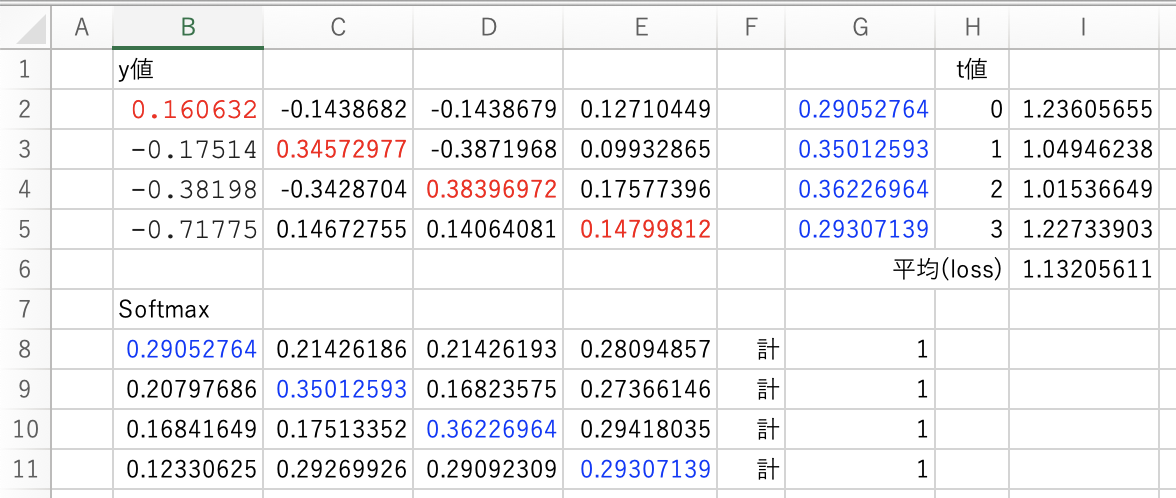
G列の値は、t値を索引(0=B列、1=C列、2=D列、3=E列)として分子として値を求めます。
I列はG列の値を使用して誤差$=-log(Gn)$を求めます。
I列の平均値がlossの値となり、実際に出力結果と値が一致しています。
t値(0-3)は正解ラベルなので、赤字の値は各行での最大値になっています。
最大値の位置が正解ラベルとズレていれば精度(accuracy)が 1.0 にならないわけです。
$\begin{align}\operatorname*{CrossEntropy}(\boldsymbol{p}, \boldsymbol{q}) = - \sum_{k = 1}^K p_k \log q_k\end{align}$
# G2の計算
=EXP(B2)/(EXP(B2)+EXP(C2)+EXP(D2)+EXP(E2))
# I2の計算
=-LN(G2)
# G3の計算
=EXP(C3)/(EXP(B3)+EXP(C3)+EXP(D3)+EXP(E3))
# I3の計算
=-LN(G3)
# G4の計算
=EXP(D4)/(EXP(B4)+EXP(C4)+EXP(D4)+EXP(E4))
# I4の計算
=-LN(G4)
# G5の計算
=EXP(E5)/(EXP(B5)+EXP(C5)+EXP(D5)+EXP(E5))
# I5の計算
=-LN(G5)
# I6の計算 平均(loss)
=AVERAGE(I2:I5)
ソフトマックス関数(Softmax function、もしくは正規化指数関数: Normalized exponential function)とは、複数の出力値の合計が1.0(=100%)になるように変換して出力する関数である。各出力値の範囲は0.0~1.0となる。
[活性化関数]ソフトマックス関数(Softmax function)とは?
Softmaxの値の求め方はG列と同様で、G列の分子が最大値(t値)だったのに対し連番で求めます。
先頭行だけ計算方法を記載します。
$y_i =\dfrac{e^{x_i}}{\sum_{j=1}^N e^{x_j}}$
# B8の計算
=EXP(B2)/(EXP(B2)+EXP(C2)+EXP(D2)+EXP(E2))
# C8の計算
=EXP(C2)/(EXP(B2)+EXP(C2)+EXP(D2)+EXP(E2))
# D8の計算
=EXP(D2)/(EXP(B2)+EXP(C2)+EXP(D2)+EXP(E2))
# E8の計算
=EXP(E2)/(EXP(B2)+EXP(C2)+EXP(D2)+EXP(E2))
# G8の計算
=SUM(B8:E8)
調査結果
「N bit の 2進数で表される $2^N$ 個の数字を $2^N$個のOutputのどれかを1にするということを学習させる。」
2 bit の 2進数で表される 4 個の数字を 4個のOutputのどれかを1にするということを学習させる。
出力の数の意味は、活性化関数にSoftMaxを使ったために$2^N$個必要となった。正解ラベルが0からの連番になっているのはSoftMax用の索引として使用されるため。$2^N$以上の値を正解ラベルに使うと索引で値が取れないためエラーになる。
最後に
機械学習で論理演算(AND,OR,XOR)をやった後だったために、その知識に引きづられてしまった。理解してみれば言っている意味は分かったけど、そこに到達するまでに一苦労である。
Chainerの開発は終了してしまったけど、機械学習がブームになったころは日本産のChainerがよく使われていたので、昔の記事で勉強になるものでもChainerが使用されている。TensorFlowなど他のライブラリーに移植するにしても根本的に理解してないと詰まる。