はじめに
先日ChainerというDeepLearning用のフレームワークが公開されました。
Chainerは Pythonで非常に多種多様なDeepLearningの構造を簡潔に表現して、学習・評価をすることができる素晴らしいソフトウェアだと思います。
王道な使い方はChainerのチュートリアルや下記記事などを見るとよくわかると思います。
【機械学習】ディープラーニング フレームワークChainerを試しながら解説してみる。
私は子供の頃からAIのようなものに憧れていて、特に GoogleのDQN は非常に驚きました。
ブロック崩しのようなゲームにおいて「ピクセルとゲームスコアの情報のみがフィードバックとして与えられた」AIが人間を凌駕する腕前に成長するとかちょっと何言っているのかわからない感じに凄いです。
そういうものはどのようにしたら実現できるのか、という興味から、
どういう問題ならDeepLearningで学習できるのか(私の技術レベルで ^^;)というのを
このChainerを使って探っていきたいと思います。
最終的には簡単なシミュレータ(言ってみればある種のゲーム)を操作する用なものが作れたら良いなぁと思います。
まあ、いきなり難しいことをやるのは大変なので、非常に簡単なモノから試していこうと思います。
お題:2進法を学習できるか?
問題
今回は N bit の入力を、対応する $2^N$個のどれかに出力するという問題を考えます。
中間の隠れ層は1層(H1)、もしくは、無しで試してみます。図にしてみるとこんな感じです。
実験
使っているのは Chainer の基本的な機能だけなので説明は省きます。
実験用のソースコードはこちらになります。
仕様がわかっていなかったので、学習用のデータを手作りするのが少し手間取りました。
F.softmax_cross_entropy(y, t) F.accuracy(y, t) では
- yは: 2次元で dtype=np.float32 の numpy.array を Variable にしたもの
- tは: 1次元で dtype=np.int32 の numpy.array を Variable にしたもの
を作る必要がありました。
ドキュメントもそれなりに充実していますし、わからないときはドキュメントからリンクされているChainerのソースコード を見るとある程度簡単に調べられます。
結果
最初N=4で実験してみると中間層H1なしでもあっさり学習出来ました(正答率100%)。
当然H1を増やしても学習可能です。
ここで躓いたらどうしようと思っていましたが、とりあえず良かったです。
Bit数と学習回数
Nはどこまでいけるのかな、と思い、N=5,6,7 と増やしていくと学習にかかる時間(回数)が増えていきました。
中間層が無い場合にNを変化させた時の学習回数は以下のようになりました。

指数オーダーで増えていく感じに見えます。結果が出てみるとある意味納得です。
中間層H1の効果
中間層をある程度与えると、学習にかかる回数が減っていきます。
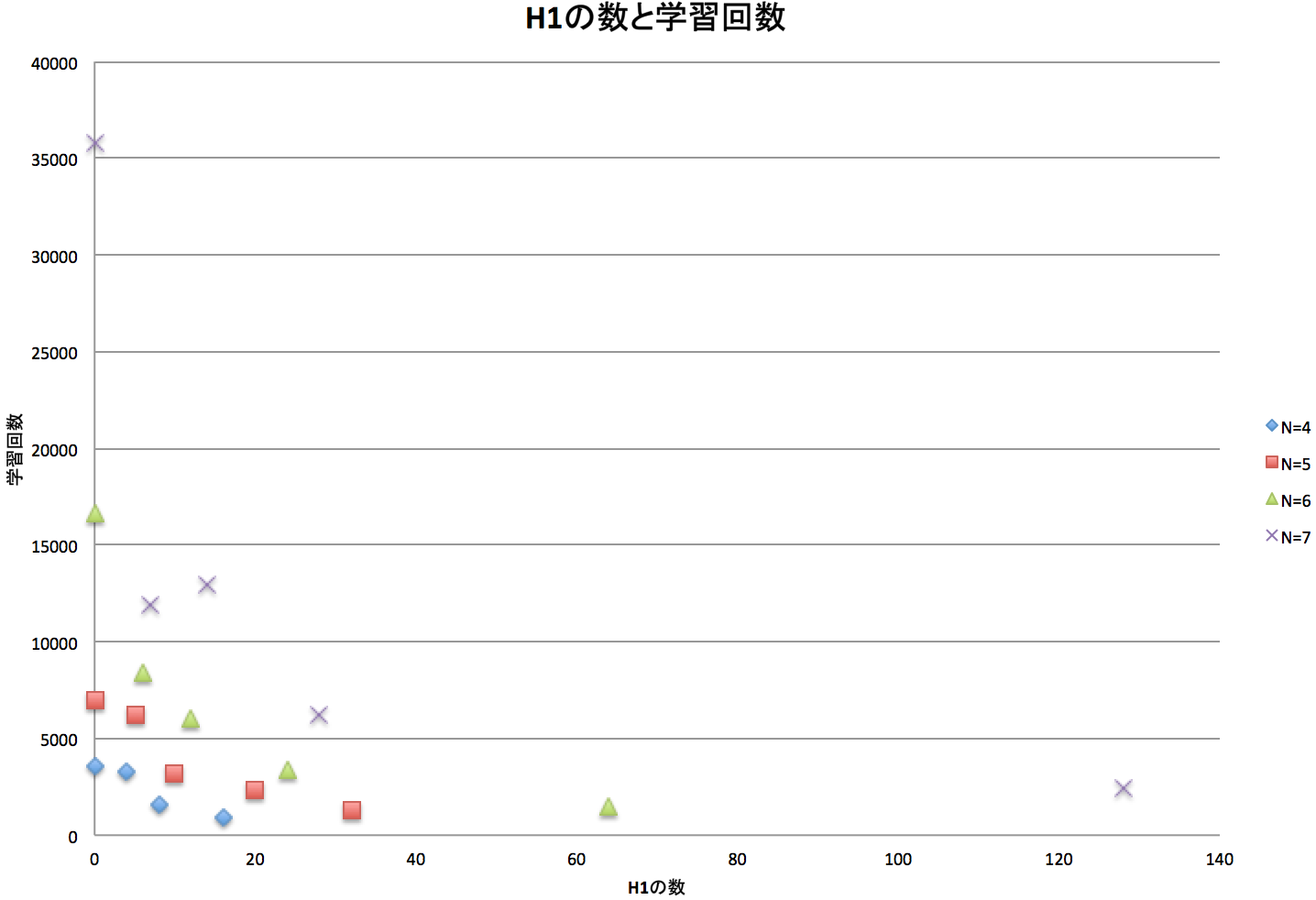
それをまとめたのが以下のグラフになります。
Excelが苦手でちょっと見にくいですが、H1がある程度ある方が早く学習が終わることが見て取れます。
生結果
| N(bit) | H1 size | 回数 |
|---|---|---|
| 4 | 0 | 3567 |
| 4 | 4 | 3285 |
| 4 | 8 | 1586 |
| 4 | 16 | 947 |
| 4 | 16 | 914 |
| 5 | 0 | 6948 |
| 5 | 5 | 6219 |
| 5 | 10 | 3216 |
| 5 | 20 | 2303 |
| 5 | 32 | 1336 |
| 6 | 0 | 16606 |
| 6 | 6 | 8360 |
| 6 | 12 | 6076 |
| 6 | 24 | 3392 |
| 6 | 64 | 1447 |
| 7 | 0 | 35822 |
| 7 | 7 | 11889 |
| 7 | 14 | 12936 |
| 7 | 28 | 6192 |
| 7 | 128 | 2459 |
さいごに
Chainerお手軽で楽しいです。
できて当然のようなことでも、なんか実際にできると嬉しいです。