ディープラーニングを使ってロト6の数字でも予想してみようかという遊びです。
もちろんロトは毎回ランダムな数字を出しているだけなので上手くいくはずないんですが、真剣に予想されている方もいるようだし、ササッとコードも書いてしまったので、HDDに埋めておくよりは公開しておきます。
あまり真剣にやってないので、解説も適当です。気になることがあればコメントください。
目標
- ロト6の当選番号予測。
※ロト6を選んだのは、私が唯一買ったことがある数字当て系宝くじだからです。
概要
入力はどーしようかと思ったのですが、過去5回分くらいの当選番号としました。
ロト6は、43個の数字の中から6つが選んで、6つ全部当たれば1等賞というような仕組み。ですので、出力としては43個のフラグで、例えば1,3,4,11,20,43が当選番号の場合、[1,0,1,1,0,0,.....0,0,1]みたいなフラグを予想するものとしました。(厳密にはSoftmaxを通すので少し違いますが)
データはみずほ銀行のHPよりスクレイピングして集めました。大体1000個くらいのデータになります。
環境
TensorFlow 0.7
Ubuntu 14.04
AWS EC2 microinstance
実装
ポイントとなりそうなところだけ抜粋します。
隠れ層は2つ、ユニット数はそれぞれ1000と500。出力は43です。
def inference(x_ph, keep_prob):
with tf.name_scope('hidden1'):
weights = tf.Variable(tf.truncated_normal([data_num * NUM_CLASSES, NUM_HIDDEN1], stddev=stddev), name='weights')
biases = tf.Variable(tf.zeros([NUM_HIDDEN1]), name='biases')
hidden1 = tf.nn.relu(tf.matmul(x_ph, weights) + biases)
with tf.name_scope('hidden2'):
weights = tf.Variable(tf.truncated_normal([NUM_HIDDEN1, NUM_HIDDEN2], stddev=stddev), name='weights')
biases = tf.Variable(tf.zeros([NUM_HIDDEN2]), name='biases')
hidden2 = tf.nn.relu(tf.matmul(hidden1, weights) + biases)
# DropOut
dropout = tf.nn.dropout(hidden2, keep_prob)
with tf.name_scope('softmax'):
weights = tf.Variable(tf.truncated_normal([NUM_HIDDEN2, NUM_CLASSES], stddev=stddev), name='weights')
biases = tf.Variable(tf.zeros([NUM_CLASSES]), name='biases')
y = tf.nn.softmax(tf.matmul(dropout, weights) + biases)
return y
損失計算部分。
正解のラベル(target)は0か1かのフラグになっていますが、yはsoftmaxを通してくるので全体として足し合わせて1となるハズで、このままだとスケールが合わないのでtargetもsoftmaxを通します。
def loss(y, target):
softmax_target = tf.nn.softmax(target)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, softmax_target, name='xentropy')
loss = tf.reduce_mean(cross_entropy, name='xentropy_mean')
return loss
訓練。
def training(sess, train_step, loss, x_train_array, y_train_array):
summary_op = tf.merge_all_summaries()
init = tf.initialize_all_variables()
sess.run(init)
summary_writer = tf.train.SummaryWriter(LOG_DIR, graph_def=sess.graph_def)
for i in range(int(len(x_train_array) / bach_size)):
batch_xs = getBachArray(x_train_array, i * bach_size, bach_size)
batch_ys = getBachArray(y_train_array, i * bach_size, bach_size)
sess.run(train_step, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 0.8})
ce = sess.run(loss, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 1.0})
summary_str = sess.run(summary_op, feed_dict={x_ph: batch_xs, y_ph: batch_ys, keep_prob: 1.0})
summary_writer.add_summary(summary_str, i)
結果
損失
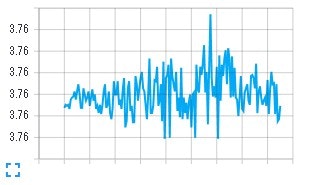
見事にどーにもなっていないことが分かります(笑)
どーしようもないとこのような感じになるんだなということが勉強になりました。
予測
全くダメなのは分かっていますが、実際に予測してみましょう。
第1045回~第1041回のデータを使い、第1046回を予測してみます。
入力は下記な感じで、
[[01,19,21,30,31,43],[03,07,16,26,34,39],[21,29,30,32,38,42],[04,10,11,12,18,25],[14,22,27,29,33,37]]
結果は下記。
[6, 10, 12, 23, 27, 38]
実際の当選番号は[06, 13, 17, 18, 27, 43]。
2つ当たってます。ちなみに3つ当たって千円です。
何個くらい当たるのが平均なのかよく分かりませんが(どうやって計算するのか分からない)、変な期待は捨てましょう。