FReLUを過去の活性化関数と比較する

紹介する論文

Funnel Activation for Visual Recognition (ECCV 2020)

論文は以下のURLから参照してください！
https://www.ecva.net/papers/eccv_2020/papers_ECCV/papers/123560341.pdf

論文の概要

FReLUという畳み込み層を使った「画像（2D空間）系」専門の新たな活性化関数を提案し、これが広範囲のデータセットで有効であることを示した。

活性化関数の歴史

そもそも活性化関数とは

活性化関数とは、ニューラルネットワークのニューロン間でやりとりする際に、その情報を加工する関数のことである。
動物の脳におけるニューラルネットワークでも、シナプス間は電気ではなく化学物質の放出によって情報を伝播するので、情報を変形していると言える。

ニューラルネットワーク全体の表現力を増すため、非線形関数が用いられるのが一般的である。

FReLU以前の活性化関数

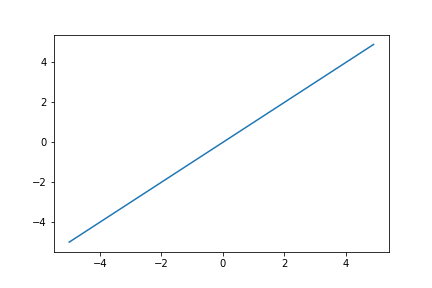
恒等関数

$f(x)=x$

$f'(x)=1$

これは線形関数である。（使われない）

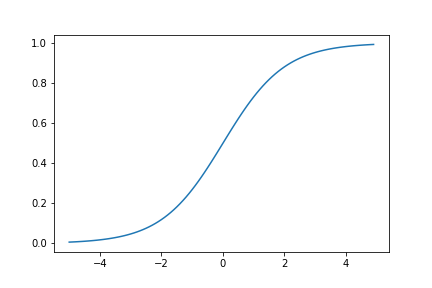
Sigmoid関数

$f(x)=\frac{1}{1+e^{-x}}$

$f'(x)=f(x)(1-f(x))$

入力がかなり大きかったり逆に小さかったりすると勾配が消失する。また微分の値も全体的に小さい。

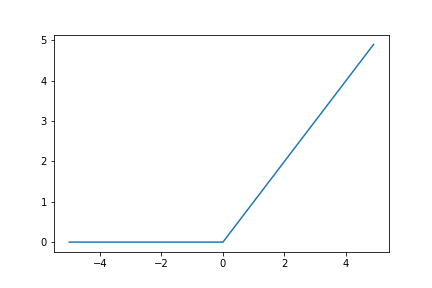
ReLU関数

$f(x)=max(x,0)$

$f'(x) =
\begin{cases}
1 & (x\geq 0) \\
0 & (x<0)
\end{cases}$

微分が入力に依存しないため、層を深くしても勾配が消失しない。しかし、入力が負になると勾配が消失する。

Leaky ReLU関数

$f(x)=max(x, \alpha x)$
$\alpha$は0.01などの小さい値にする。

$f'(x) =
\begin{cases}
1 & (x\geq 0) \\
\alpha & (x<0)
\end{cases}$

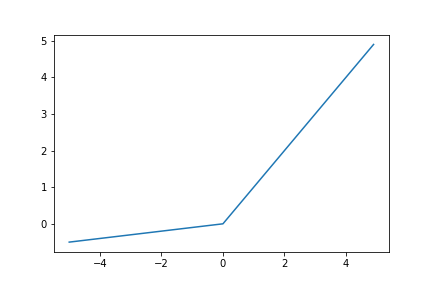
（ReLUとの違いが分かるように画像は$\alpha = 0.1$であるが、実際はもう少し小さい値が採用される。）
入力が負になると勾配が消失するというReLU関数の問題点を解決する。

PReLU関数

$f(x)=max(x, \alpha x)$
ただし、$\alpha$は学習するパラメータになる。
$f'(x)$はLeaky ReLUと同様である。

入力が負になると勾配が消失するというReLU関数の問題点を解決する。また、パラメータが更新されるため、モデルの柔軟性が増す。

論文の内容

この論文ではまず畳み込み層の有用性を強調しており、普通の畳み込み層でより複雑な画像を認識したいと述べている。また、ReLU関数の有用性についても指摘しており、これを組み合わせることが望ましいと述べている。そこで、新たな活性化関数であるFReLU関数を提案した。

$f(x)=max(x, T(x))$

ただし、$T(x)$は畳み込み層のことである。この畳み込み層のパラメータはモデルと一緒に学習させる。

まず、この関数はmax関数で非線形性を表現している。これは現在最も使われているReLU関数に影響を受けていると論文中で述べられている。

次に、この畳み込み層の領域は、よく使われる正方形の畳み込み層に限定する必要はない。論文中では三角や丸なども可能性として挙げられている。ただし、今回はよく使われる正方形の領域を採用している。

最後に、この活性化関数は「非線形性」と「空間依存性（局所性）」を初めて同時に提供している。それ以前の手法はこの二つを別々の形で提供していた（畳み込み層（空間依存性）とReLU活性化（非線形性）など）のとは対照的だ。

論文中では画像分類、物体認識、セマンティックセグメンテーションという画像系の主要なタスク全てにFReLUが有効であることを示している。データセットもImageNet, MobileNetなどの比較的大きなデータセットを用いているため、研究の信頼性が増している。

今回書いたコードの内容

cifar10の分類問題を解く深層学習モデルで評価する。

import numpy as np
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

print("Training Start")

# バッチサイズは1024にする。
batch_size = 2**10
# データセットの変換を定義する。平均と標準偏差を加工する。
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

# CIFAR10のデータセットのダウンロードをする。download=Trueにすると自動的にダウンロードをする。
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=False, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=2)

print(trainset.data.shape)

以下のような簡単なモデル（畳み込み層3層+全結合層1層)で、50epoch学習を試みる。論文中では広い範囲のモデルに適用できると述べているため、論文中では示されていない、Resnet以前のより簡単なモデルでの効果を検証するという意義もある。

class Model_(活性化関数の名前）(nn.Module):
    def __init__(self, nf, nc, num_class):
        super(Model_Sigmoid, self).__init__()
        self.main= nn.Sequential(
            nn.Conv2d(nc, nf*4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(nf*4),
            活性化関数,
            nn.Conv2d(nf*4, nf*2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(nf*2),
            活性化関数,
            nn.Conv2d(nf*2, nf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(nf),
            活性化関数,
            nn.Flatten(),
            nn.Linear(nf*nf*2, num_class)
        )

    def forward(self, input):
        return self.main(input)

学習中、毎epochの損失とtop1正解率を記録し、学習の推移を可視化できるようにする。学習の進行の内容は以下のコードを参照してください。

# 公式実装

import torch.optim as optim

# モデルごとの損失とtop1正解率を格納する。
losses_array=[]
accs_array=[]

for net in nets:

    criterion = nn.CrossEntropyLoss()
    # 確率的効果法によって学習中に柔軟に学習係数を変化させる。
    optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

    loss_array=[]
    acc_array=[]

    for epoch in range(50):

        running_loss = 0.0
        i_save =0
        sum_epoch= 0
        for i, data in enumerate(trainloader, 0):
            i_save+=1
            # 画像と画像ラベルを読み出し、それをGPUに載せるのであれば載せる。
            inputs, labels = data
            inputs = inputs.to(device)
            labels = labels.to(device)

            # 学習を進行させる。
            optimizer.zero_grad()
            outputs = net(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()

            # 損失と正解率を加算する。
            running_loss += loss.item()
            arg_1 = torch.argmax(outputs ,dim = 1)
            sum_epoch+=torch.sum(labels ==arg_1)
        # 損失と正解率を記録する。
        print(f'[{epoch + 1}, {i_save + 1:5d}] loss: {running_loss / i_save:.3f} acc: {sum_epoch / (trainset.data.shape[0]):.3f}')
        loss_array.append(running_loss / i_save)
        acc_array.append(sum_epoch / (trainset.data.shape[0]))
        
        running_loss = 0.0
        sum_epoch = 0


    print('Finished Training')
    losses_array.append(loss_array)
    accs_array.append(acc_array)

詳しくはgithubから見てください！
https://github.com/yahiro-code/FReLU

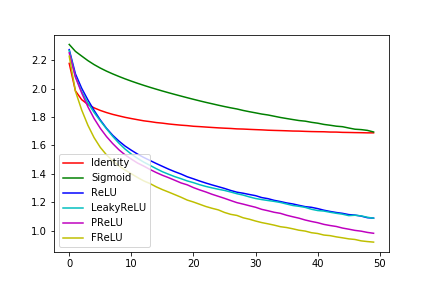
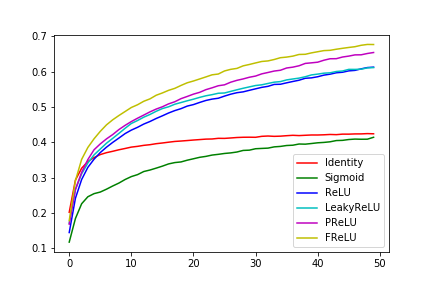
結果

　損失のグラフ

（縦軸が損失、横軸がepoch）

top1正解率のグラフ

（縦軸が正解率、横軸がepoch）

性能として、
FReLU > PReLU > LeakyReLU >= ReLU >> Sigmoid >> Identity
という結果になっている。

考察

まず、線形活性化関数のIdentity関数は早期に学習が終了してしまい、性能も良くない。
また、Sigmoid関数の実験結果は学習の進行がReLU関数に比べて遅いことを示しており、これはSigmoid関数の傾きが小さすぎるところがあることが学習に悪影響を与えていることを示唆している。
ReLU系の中で、FReLUが一番学習の進行が早く、これは論文の優位性を示している。（自前の環境ではGPUの性能が良くないため、50epochぐらいが限界であるが、まだまだ性能が上がりそうである。）

まとめ・感想

FReLUは画像系のタスクにおいて有効な畳み込み層を用いた新たな活性化関数である。これは小さなモデルでも同様の効果を示している。
機械学習の深層モデルの改良として、活性化関数の改良があげられるのにまず驚いた。さらに、活性化関数の中でも畳み込み層を使うという着眼点にも驚かされた。この着眼点の素晴らしさは、実装と計算量自体は昔からできるはずであるのにもかかわらず、ECCV2020という比較的最近の会議で採択されているところからも伺える。論文中で示されている「幅広いデータセットとタスクでの応用可能性」は非常に魅力的であるため、この研究は重要であると考える。後続研究にも期待したいところである。