前回に引き続きMDR社のblueqatのチュートリアルに掲載されている、交通最適化問題を解いていきたいと思います。
今回はD-waveとVolks Wagenが共同で行なった研究資料とこちらの記事も参考にしています。
blueqatのチュートリアルはこちらからどうぞ。
交通最適化問題とは
交通最適化問題とは、「交通渋滞を予測し、その解消を目的とした最適なルートをとる」問題です。
Q_{v, j} =
\left\{
\begin{array}{ll}
1 & (車vがルートjを通る) \\
0 & (車vがルートjを通らない)
\end{array}
\right.\\
s = 道 \\
# = ルート \\
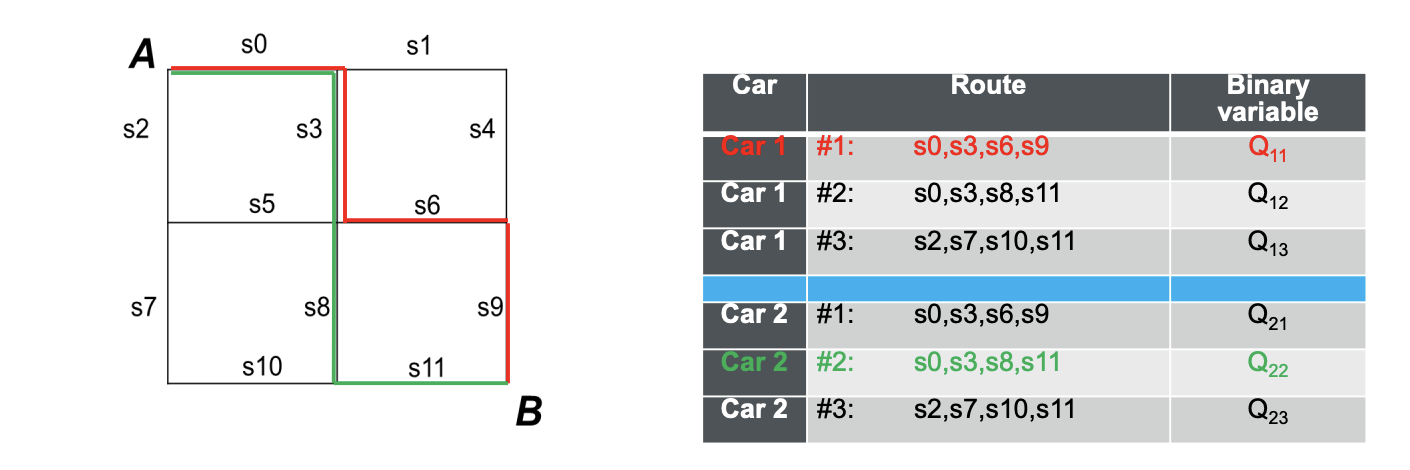
このように、それぞれの車(Car1, Car2)が、A地点からB地点まであらかじめ決められたルート(#1, #2, #3)の中から、どこを通るのが最も渋滞が起きないかを考えていきます。
もちろん今回は#1と#2がs0, s3を共通で持ち、#2と#3がs11を共通で持つため、どちらかのCarが#1、もう一方が#3を通ることで最も渋滞を緩和することができます。
また以下では具体例にCar1が赤いルートを、Car2が緑のルートを通っているものとして考えていきます。
目的関数
では早速今回の目的関数をみてみましょう。
H = \sum_s{(\sum_v\sum_j\sum_{s_j}Q_{v, j})^2}+K\sum_v{(1-\sum_jQ_{v, j})^2}
上述のようになります。
また、QUBOマトリクスは以下のようになります。
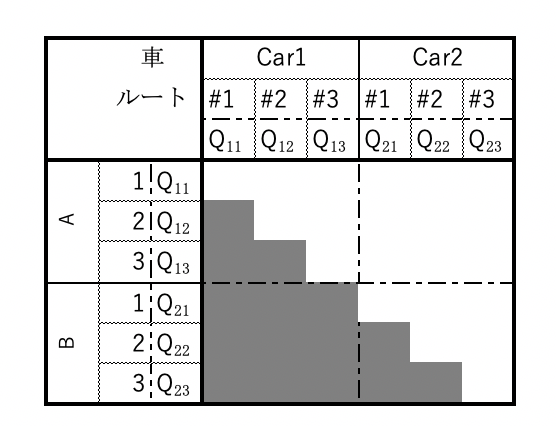
では1項ずつ噛み砕いていきましょう。
第1項:ルートの重複を調べる
\sum_s{(\sum_v\sum_j\sum_{s_j}s_jQ_{v, j})^2}\\
s_j =
\left\{
\begin{array}{ll}
1 & (ルートjが道sを含む) \\
0 & (ルートjが道sを含まない)
\end{array}
\right.\\
この項はそれぞれの道$s$に関して、$Q$の和を調べるコスト関数です。
具体例を用いると、以下のようになります。
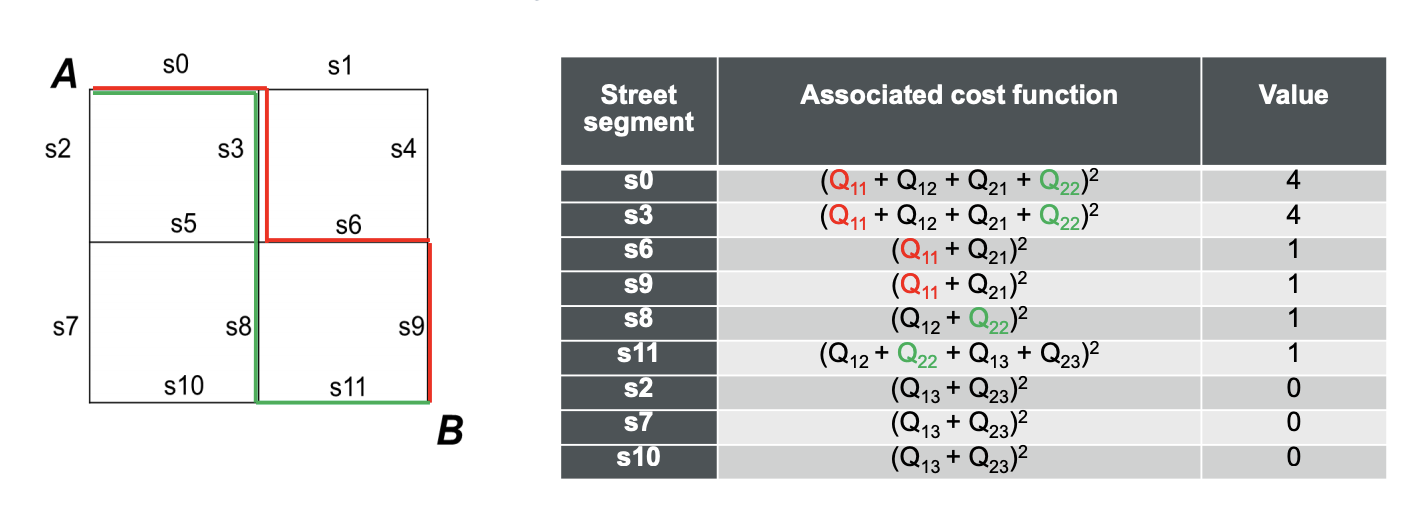
今回の例では、$Q_{11} = Q_{22} = 1$でそれ以外の全ての$Q = 0$になります。
よって$4+4+1+1+1+1+0+0+0 = 12$が今回の第1項のコストになります。
これを多項式的に書くと、
(Q_{11} + Q_{12} + Q_{21} + Q_{22})^2 + (Q_{11} + Q_{12} + Q_{21} + Q_{22})^2
+ (Q_{11} + Q_{21})^2 + (Q_{11} + Q_{21})^2\\
+ (Q_{12} + Q_{22})^2 + (Q_{12} + Q_{22} + Q_{13} + Q_{23})^2 + (Q_{13} + Q_{23})^2
+ + (Q_{13} + Q_{23})^2 + (Q_{13} + Q_{23})^2
となり、これを展開した時のそれぞれの係数をQUBOに変形させると、
 となります。
となります。
第2項:各車は1つしかルートを取らない
K\sum_v{(1-\sum_jQ_{v, j})^2}\\
K = 重み(ハイパーパラメータ)
この項は、それぞれの車が複数のルートをとるときに値が増加するペナルティ関数です。
多項式的に書くと、
K(1-(Q_{11}+Q_{12}+Q_{13}))^2+K(1-(Q_{21}+Q_{22}+Q_{23}))^2
となります。
つまり今回の例では、
K(1-(1+0+0))^2+(1-(0+1+0))^2 = 0
となり、各々の車が複数のルートを走っていないことがわかります。
ではこれをQUBOに変換していきましょう。

これで各項のQUBOが出揃いました。
総和
第2項に重み$K$をかけることを忘れずに、全体のQUBOを算出してみます。

あとはこれをアニーリングマシンにぶち込めば最適解が出てくるので、実際に試してみましょう。
実装
では以上で出たQUBOをPythonで実現してみましょう。
必要なモジュールは以下の2つです。
import blueqat.opt as wq
import numpy as np
入力セル
pu_cost_matrix = [[1,1,0,1,1,0],[1,1,0,1,1,0],[1,0,0,1,0,0],[1,0,0,1,0,0],[0,1,0,0,1,0],[0,1,1,0,1,1],[0,0,1,0,0,1],[0,0,1,0,0,1],[0,0,1,0,0,1]]
print("Number of cars:")
pu_cars_size = int(input())
pu_roots_size = int(len(pu_cost_matrix[0])/pu_cars_size)
print("The cost of constraint:")
pu_K = float(input())
print("The cost of traffic qubo:")
pu_A = float(input())
・pu_cost_matrixはそれぞれの道$s$を通るルートを表したもの(今回はベタ打ちしてます)
・pu_cars_sizeは車の数(今回は2を入力)
・pu_roots_sizeはルートの数
・pu_Kは重み$K$の大きさ(今回は10を入力)
コスト関数:第1項
def get_traffic_qubo(cars_size, roots_size, K):
qubo_size = cars_size*roots_size
traffic_qubo = np.zeros((qubo_size, qubo_size))
indices = [(u, v, i, j) for u in range(cars_size) for v in range(cars_size) for i in range(roots_size) for j in range(roots_size)]
for u, v, i, j in indices:
ui = u * roots_size + i
vj = v * roots_size + j
if ui > vj:
continue
if ui == vj:
traffic_qubo[ui][vj] -= K
if u == v and i != j:
traffic_qubo[ui][vj] += 2 * K
return traffic_qubo
traffic_qubo = get_traffic_qubo(pu_cars_size, pu_roots_size, pu_K)
コスト関数:第2項
def get_traffic_cost_qubo(cost_matrix):
traffic_cost_qubo = np.zeros((len(cost_matrix[0]), len(cost_matrix[0])))
for i in range(len(cost_matrix)):
traffic_cost_qubo += wq.sqr(cost_matrix[i])
return traffic_cost_qubo
traffic_cost_qubo = get_traffic_cost_qubo(pu_cost_matrix)
観測セル
def get_traffic_optimisation(traffic_qubo, traffic_cost_qubo):
a = wq.opt()
a.qubo = traffic_qubo + traffic_cost_qubo
answer = a.sa()
print(answer)
a.plot()
return answer
出力セル
traffic_qubo = get_traffic_qubo(pu_cars_size, pu_roots_size, pu_K)
traffic_cost_qubo = get_traffic_cost_qubo(pu_cost_matrix)
q = get_traffic_optimisation(traffic_qubo, traffic_cost_qubo)
[1, 0, 0, 0, 0, 1]
 このように$Car1$でルート1を、$Car2$でルート3をとっているのでうまく答えを導けていることがわかります。
このように$Car1$でルート1を、$Car2$でルート3をとっているのでうまく答えを導けていることがわかります。
では、前回同様にハミルトニアンの検証を行います。
ハミルトニアンの検証
def calculate_H_f(q, cost_matrix):
H_f = 0
for vi in range(len(q)):
if q[vi] == 1:
H_list = []
for k in range(len(cost_matrix)):
H_list.append(cost_matrix[k][vi])
np.square(H_list)
H_f += np.sum(H_list)
print(H_f)
return H_f
def calculate_H_s(q, cars_size, roots_size):
H_s = 0
for v in range(cars_size):
sum_x = 0
for i in range(roots_size):
index = v * roots_size + i
sum_x += q[index]
H_s += (1 - sum_x) ** 2
print(H_s)
return H_s
def calculate_H(q, cities_size, cost_matrix, roots_size, K):
print("hamiltonian_f =")
H_f = calculate_H_f(q, cost_matrix)
print("hamiltonian_s =")
H_s = calculate_H_s(q, cities_size, roots_size)
H = H_f + H_s * K
print("hamiltonian =")
print(H)
return H
ここで出力セルもちょっといじります。
traffic_qubo = get_traffic_qubo(pu_cars_size, pu_roots_size, pu_K)
traffic_cost_qubo = get_traffic_cost_qubo(pu_cost_matrix)
q = get_traffic_optimisation(traffic_qubo, traffic_cost_qubo)
calculate_H(q, pu_cars_size, pu_cost_matrix, pu_roots_size, pu_K)
すると今回の$hamiltonian = 8$であったことがわかりました。
これは、$Car1$がルート1、$Car2$がルート3をとる時の第1項を計算した値と一致するので今回もうまく最適解を導き出せていることがわかります。
まとめ
最適な道路網の形成に最も重要な「混雑状況の緩和」において、非常に早く解を求めることができました。
このトピックは土木を専攻している自分にとって非常に面白い内容だったので、今後さらに掘り下げていこうと思います。