LoginSignup
28
16

More than 1 year has passed since last update.

@yaegaki

[Unity]Quaternionからオイラー角に変換する

Last updated at Posted at 2021-10-23

Unityでは回転を表現するためにQuaternionを使用しています。
Quaternionとオイラー角は相互に変換可能で以下のように行います。

// オイラー角からQuaternionを作成する
var quaternion = Quaternion.Euler(30, 0, 0);
// Quaternionからオイラー角を作成する
var eulerAngles = quaternion.eulerAngles;

しかしQuaternionからオイラー角を作成したときに元々のオイラー角と違う値になる可能性があります。

// X軸で100度回転する
var eulerAngles = new Vector3(100, 0, 0);
var quaternion = Quaternion.Euler(eulerAngles.x, eulerAngles.y, eulerAngles.z);
// Quaternionに変換した後にオイラー角に変換しただけなので同じもののはず
var eulerAngles2 = quaternion.eulerAngles;

Debug.Log(eulerAngles2);
// (80.0, 180.0, 180.0) <= X軸で100度回転ではなくなっている!

今回の記事ではなぜこのようになるのかについて解説します。

同じ回転を表すオイラー角

同じ回転を表すオイラー角は 基本的に2つ あります。
例えば (100, 0, 0) と (80, 180, 180) は同じ回転を表します。
1つのオイラー角が判明しているとき、もう片方のオイラー角は以下の方法で求めることができます。

// 同じ回転を表すオイラー角を取得する
Vector3 GetSameRotationEulerAngles(Vector3 eulerAngles)
{
    // x = 180 - x
    // y = 180 + y
    // z = 180 + z
    return new Vector3(180 - eulerAngles.x, 180 + eulerAngles.y, 180 + eulerAngles.z);
}

var eulerAngles = new Vector3(80, 0, 0);
var eulerAngles2 = GetSameRotationEulerAngles(eulerAngles);
Debug.Log($"{eulerAngles}, {eulerAngles2}");
// (80.0, 0.0, 0.0), (100.0, 180.0, 180.0) <= 値は違うが回転は同じ

var rot1 = Quaternion.Euler(eulerAngles.x, eulerAngles.y, eulerAngles.z);
var rot2 = Quaternion.Euler(eulerAngles2.x, eulerAngles2.y, eulerAngles2.z);
Debug.Log($"{rot1.eulerAngles}, {rot2.eulerAngles}");
// (80.0, 0.0, 0.0), (80.0, 0.0, 0.0) <= 同じ値になっている

基本的に2つと書いた通り3つ以上存在する場合もあります。
それはX軸の回転が 90度及び-90度のとき です。
この状態を ジンバルロック と呼び同じ回転を表すオイラー角は無数に存在します。

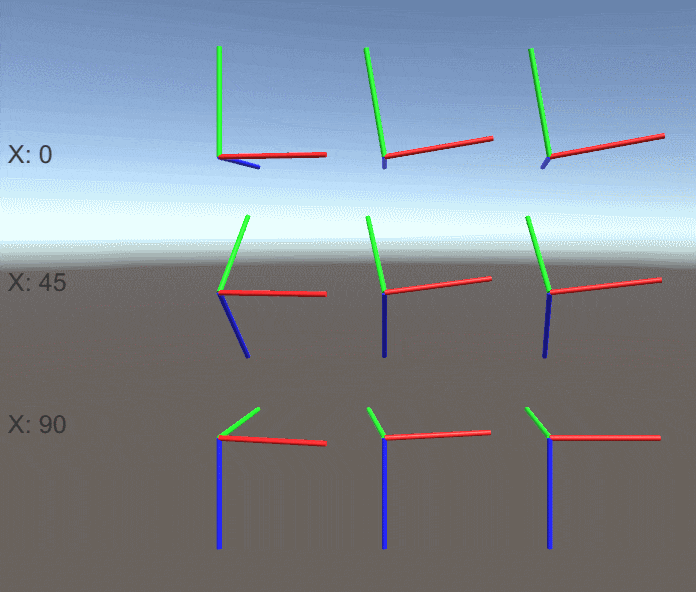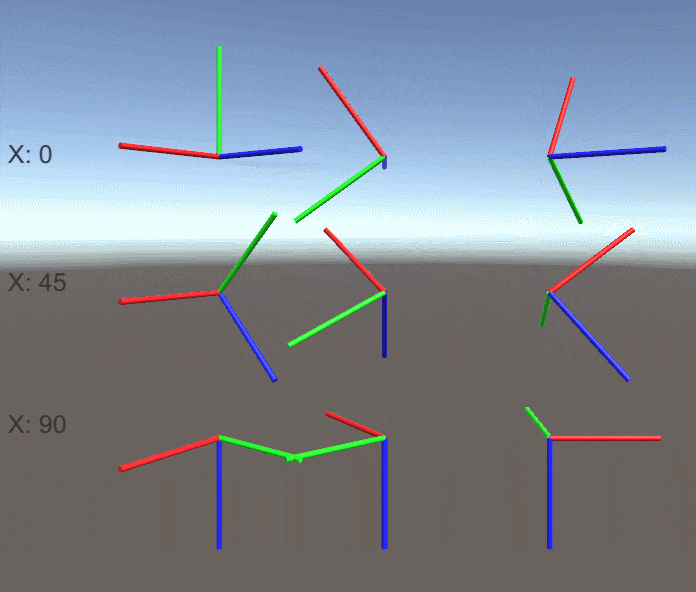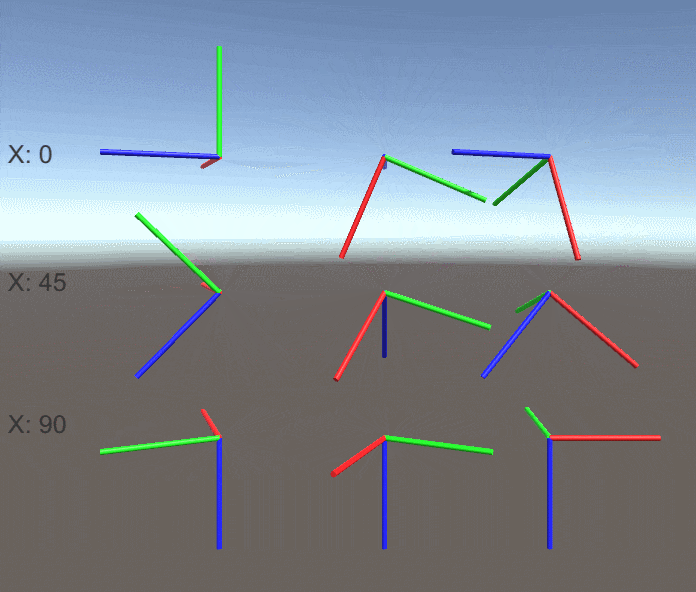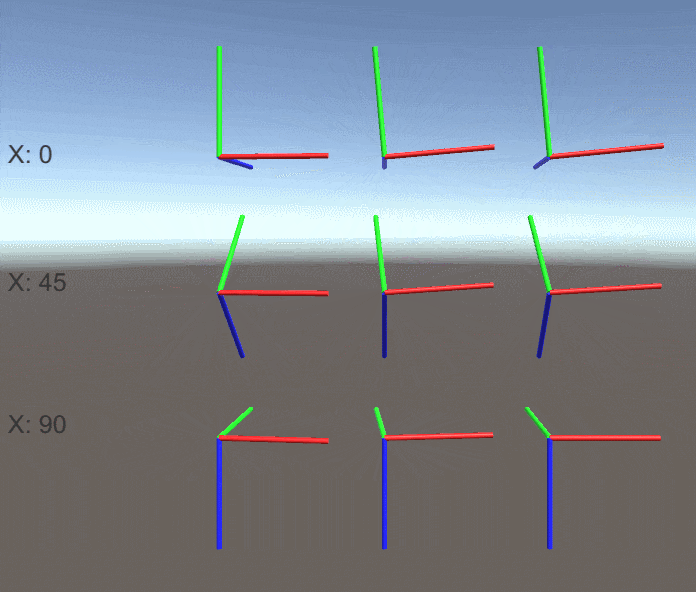
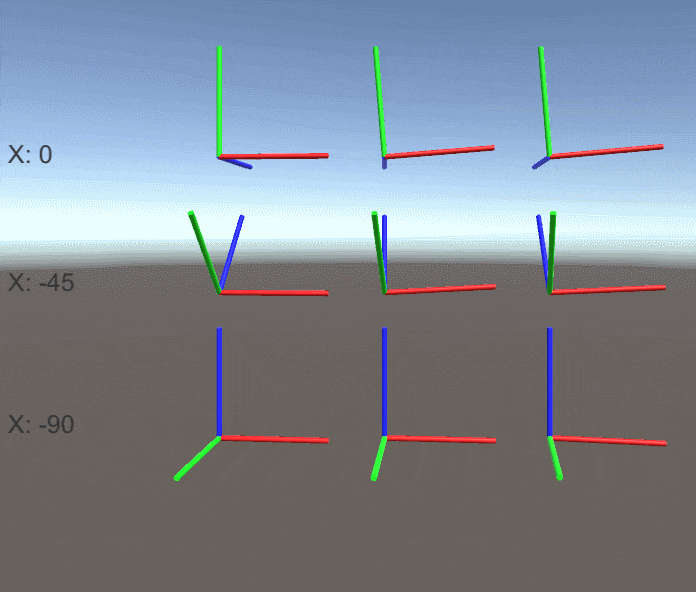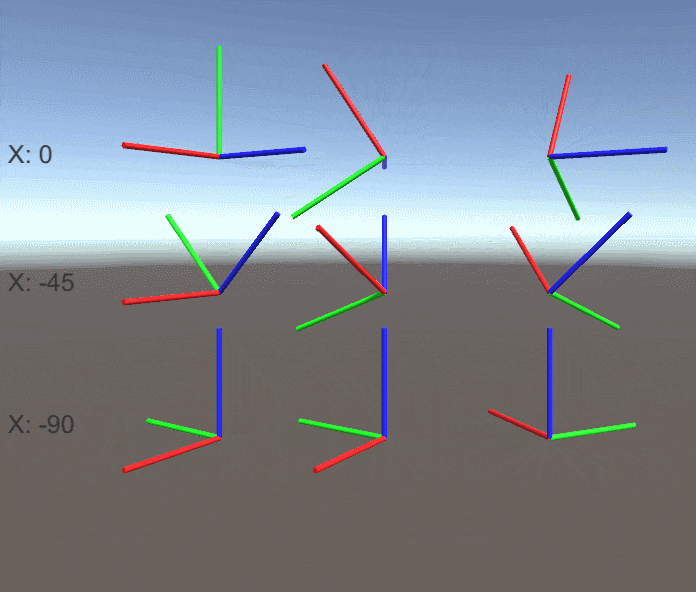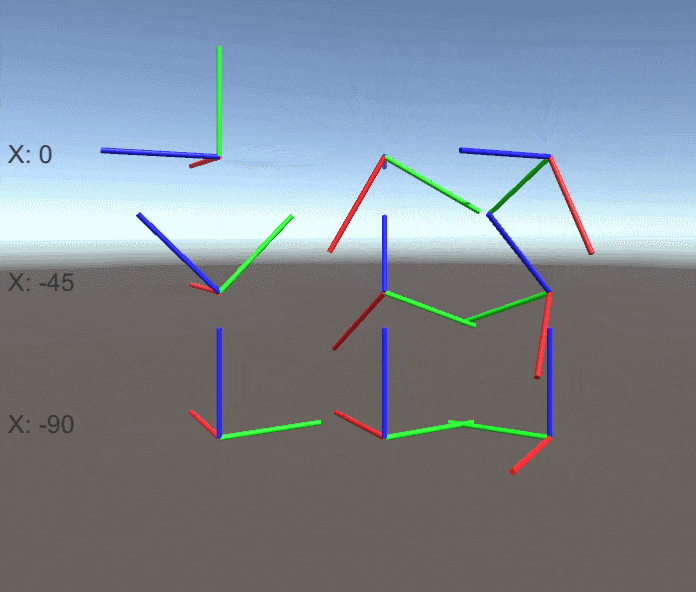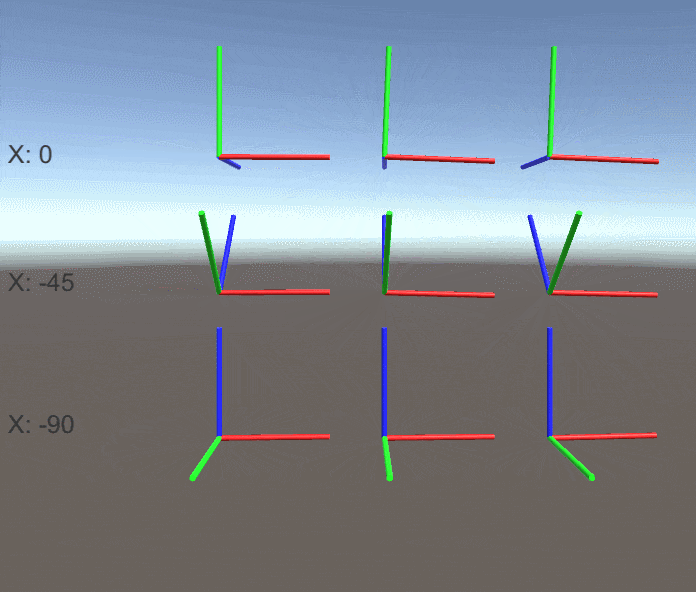
ジンバルロックついて実験してみます。
以下のコードはデフォルトのX軸回転を指定して毎フレームY軸のみ、Z軸のみ、Y軸とZ軸両方でオブジェクトを回転させます。

[SerializeField]
private float defaultX;

void Start()
{
    t1.localRotation = Quaternion.Euler(defaultX, 0, 0);
    t2.localRotation = Quaternion.Euler(defaultX, 0, 0);
    t3.localRotation = Quaternion.Euler(defaultX, 0, 0);
}

void Update()
{
    var delta = Time.deltaTime * speed;
    var angle = t1.localRotation.eulerAngles;
    angle.y += delta;
    t1.localRotation = Quaternion.Euler(angle.x, angle.y, angle.z);

    angle = t2.localRotation.eulerAngles;
    angle.z += delta;
    t2.localRotation = Quaternion.Euler(angle.x, angle.y, angle.z);

    angle = t3.localRotation.eulerAngles;
    angle.y += delta;
    angle.z += delta;
    t3.localRotation = Quaternion.Euler(angle.x, angle.y, angle.z);
}

X軸の回転が0/45/90度の時の結果を見てみましょう。

x0-45-90.gif

X軸の回転が90度のとき、 Y軸での回転とZ軸での回転がちょうど逆の回転 になってしまっています。
その結果Y軸とZ軸の両方を回転させたときの回転がゼロになってしまい固定されています。

X軸の回転が0/-45/-90度の時の結果も見てみましょう。

x--45--90.gif

X軸の回転が-90度のとき、 Y軸での回転とZ軸での回転が全く同じ回転 になってしまっています。

これらの結果からジンバルロック状態の時、Y軸とZ軸の回転を調整することで 同じ回転を表す無数の回転を作ることができる ことがわかります。
例えばX軸の回転が90度の時は Y軸とZ軸の回転の差が一定なら常に同じ回転 、X軸の回転が-90度のときは Y軸とZ軸の回転の和が一定なら常に同じ回転 になります。

Quaternionからオイラー角に変換する方法

同じ回転を表すオイラー角は少なくとも2つ以上存在することは前述の通りです。
Quaternion.eulerAngles では一体どのようにして1つのオイラー角に計算しているのでしょうか。
Unityの機能を使用せずQuaternionをオイラー角に変換することでその計算手法を考察します。

以降の内容は以下のページを参考にさせていただきました。
回転行列、クォータニオン(四元数)、オイラー角の相互変換

Quaternionをオイラー角に変換するコードは以下のようになります。

Vector3 ToEulerAngles(Quaternion q)
{
    var sinX = 2 * q.y * q.z - 2 * q.x * q.w;
    var absSinX = Mathf.Abs(sinX);

    const float e = 0.001f;

    // X軸の回転が0度付近の場合、0になるか360で差が大きいので0に丸める
    if (absSinX < e)
    {
        sinX = 0f;
    }

    var x = Mathf.Asin(-sinX);
    // X軸の回転が90度付近の場合はジンバルロック状態になっている
    if (float.IsNaN(x) || Mathf.Abs((Mathf.Abs(x) -  Mathf.PI / 2f)) < e)
    {
        x = Mathf.Sign(-sinX) * (Mathf.PI / 2f);
        return ToEulerAnglesZimbalLock(x, q);
    }

    var x = Mathf.Asin(-sinX);
    var cosX = Mathf.Cos(x);

    var sinY = (2 * q.x * q.z + 2 * q.y * q.w) / cosX;
    var cosY = (2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.z, 2) - 1) / cosX;
    var y = Mathf.Atan2(sinY, cosY);

    var sinZ = (2 * q.x * q.y + 2 * q.z * q.w) / cosX;
    var cosZ = (2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.y, 2) - 1) / cosX;
    var z = Mathf.Atan2(sinZ, cosZ);

    var angles = new Vector3(x, y, z) * Mathf.Rad2Deg;
    return new Vector3(
        Normalize(angles.x),
        Normalize(angles.y),
        Normalize(angles.z)
    );
}

float Normalize(float x)
{
    return (x > 0f ? x : 360f + x) % 360;
}

上記のコードを実行して得られるオイラー角は Quaternion.eulerAngles とほぼ一致します。
Quaternionと対応するオイラー角は2つ以上あるはずですがどうして1つのオイラー角になってしまうのでしょうか。
答えはX軸の回転角度を求める以下の部分にあります。

var x = Mathf.Asin(-sinX);

Mathf.Asin の戻り値は $-\frac{\pi}{2}\le\theta\le\frac{\pi}{2}$ なので $\theta$ が $\frac{\pi}{2}$ より大きいときや $-\frac{\pi}{2}$ より小さいときにそれを区別することができません。
つまりこの部分で 2つあるオイラー角が一つに絞られてしまっています 。

補角の公式より $\sin(\pi-\theta)=\sin\theta$ なので以下の方法でもう一つのX軸での回転も計算することができます。

var x = Mathf.Asin(-sinX);
var x2 = Mathf.PI - x;

これを踏まえたうえで2つのオイラー角を返すように ToEulerAngles メソッドを改造すると以下のようになります。

(Vector3 eulerAngles1, Vector3 eulerAngles2) ToEulerAngles(Quaternion q)
{
    var sinX = 2 * q.y * q.z - 2 * q.x * q.w;
    var absSinX = Mathf.Abs(sinX);

    const float e = 0.001f;

    // X軸の回転が0度付近の場合、0になるか360で差が大きいので0に丸める
    if (absSinX < e)
    {
        sinX = 0f;
    }

    var x = Mathf.Asin(-sinX);
    // X軸の回転が90度付近の場合はジンバルロック状態になっている
    if (float.IsNaN(x) || Mathf.Abs((Mathf.Abs(x) -  Mathf.PI / 2f)) < e)
    {
        x = Mathf.Sign(-sinX) * (Mathf.PI / 2f);
        return (ToEulerAnglesZimbalLock(x, q), ToEulerAnglesZimbalLock(x, q));
    }
    else
    {
        var x2 = Mathf.PI - x;
        return (ToEulerAngles(x, q), ToEulerAngles(x2, q));
    }
}

Vector3 ToEulerAngles(float x, Quaternion q)
{
    var cosX = Mathf.Cos(x);

    var sinY = (2 * q.x * q.z + 2 * q.y * q.w) / cosX;
    var cosY = (2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.z, 2) - 1) / cosX;
    var y = Mathf.Atan2(sinY, cosY);

    var sinZ = (2 * q.x * q.y + 2 * q.z * q.w) / cosX;
    var cosZ = (2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.y, 2) - 1) / cosX;
    var z = Mathf.Atan2(sinZ, cosZ);

    var angles = new Vector3(x, y, z) * Mathf.Rad2Deg;
    return new Vector3(
        Normalize(angles.x),
        Normalize(angles.y),
        Normalize(angles.z)
    );
}

同様に補角の公式より $\cos(\pi-\theta)=-\cos\theta$ なので Mathf.Atan2 に渡している両方の変数の符号が逆転します。

\begin{align}
-\sin\theta &= \sin(\theta+\pi) \\
-\cos\theta &= \cos(\theta+\pi) \\
\end{align}

なので

\begin{align}
\tan\theta &= \frac{-\sin\theta}{-\cos\theta} \\
\tan(\theta+\pi) &= \frac{\sin(\theta+\pi)}{\cos(\theta+\pi)}
\end{align}

Mathf.Atan2 は戻り値の範囲が $-\pi\le\theta\le\pi$なので 引数の両方の符号が反転するということと角度を $+\pi$ することが同じ意味になります。

よって同じ回転を表す2つのオイラー角は以下のように求めることができます。

\boldsymbol{\theta}=(\theta_x,\theta_y,\theta_z) \\
f(\boldsymbol{\theta}) = (\pi-\theta_x,\pi+\theta_y,\pi+\theta_z)

これをUnityで実装すると

// 同じ回転を表すオイラー角を取得する
Vector3 GetSameRotationEulerAngles(Vector3 eulerAngles)
{
    // x = 180 - x
    // y = 180 + y
    // z = 180 + z
    return new Vector3(180 - eulerAngles.x, 180 + eulerAngles.y, 180 + eulerAngles.z);
}

となります。

Quaternionからオイラー角に変換する方法(ジンバルロック)

ジンバルロックになる $\theta_x = \frac{\pi}{2}, -\frac{\pi}{2}$ それぞれのケースについて考えます。

まず $\theta_x = \frac{\pi}{2}$ の場合です。

$\theta_x = \frac{\pi}{2}$ のとき回転行列は以下のようになります。

\boldsymbol{R_{yxz}} =
\left(
  \begin{array}{ccc}
    \sin\theta_{y}\sin\theta_{z} + \cos\theta_{y}\cos\theta_{z} & \sin\theta_{y}\cos\theta_{z} -\cos\theta_{y}\sin\theta_{z} & 0 \\
    0 & 0 & -1 \\
    \cos\theta_{y}\sin\theta_{z} -\sin\theta_{y}\cos\theta_{z} & \cos\theta _{y}\cos\theta_{z} + \sin\theta_{y}\sin\theta_{z} & 0
  \end{array}
\right)\\

この回転行列は加法定理を使用することで以下のように変形できます。

\boldsymbol{R_{yxz}} =
\left(
  \begin{array}{ccc}
    \cos(\theta_{y}-\theta_{z}) & \sin(\theta_{y}-\theta_{z}) & 0 \\
    0 & 0 & -1 \\
    \sin(\theta_{z}-\theta_{y}) & \cos(\theta_{z}-\theta_{y})  & 0
  \end{array}
\right)\\

よって

\begin{eqnarray}
\tan(\theta_y-\theta_z) &=& \frac{\sin(\theta_y-\theta_z)}{\cos(\theta_y-\theta_z)} = \frac{m_{01}}{m_{00}} \\
\theta_y-\theta_z &=& \arctan(\frac{m_{01}}{m_{00}})
\end{eqnarray}

となります。

Quaternionを回転行列に変換したとき

\begin{eqnarray}
m_{00} &=& 2q_w^2 + 2q_x^2 - 1 \\
m_{01} &=& 2q_xq_y - 2q_zq_w
\end{eqnarray}

なので

\begin{eqnarray}
\theta_y-\theta_z &=& \arctan(\frac{2q_xq_y - 2q_zq_w}{2q_w^2 + 2q_x^2 - 1})
\end{eqnarray}

となります。
よって$\theta_x = \frac{\pi}{2}$ のとき $\theta_y$と$\theta_z$の差が同じであれば同じ回転を表す ことが分かります。

次に $\theta_x = -\frac{\pi}{2}$ の場合です。
$\theta_x = -\frac{\pi}{2}$ のとき回転行列は以下のようになります。

\boldsymbol{R_{yxz}} =
\left(
  \begin{array}{ccc}
    -\sin\theta_{y}\sin\theta_{z} + \cos\theta_{y}\cos\theta_{z} & -\sin\theta_{y}\cos\theta_{z} -\cos\theta_{y}\sin\theta_{z} & 0 \\
    0 & 0 & 1 \\
    -\cos\theta_{y}\sin\theta_{z} -\sin\theta_{y}\cos\theta_{z} & -\cos\theta _{y}\cos\theta_{z} + \sin\theta_{y}\sin\theta_{z} & 0
  \end{array}
\right)\\

この回転行列は加法定理を使用することで以下のように変形できます。

\boldsymbol{R_{yxz}} =
\left(
  \begin{array}{ccc}
    \cos(\theta_{y}+\theta_{z}) & -\sin(\theta_{y}+\theta_{z}) & 0 \\
    0 & 0 & -1 \\
    -\sin(\theta_{z}+\theta_{y}) & -\cos(\theta_{z}+\theta_{y})  & 0
  \end{array}
\right)\\

よって

\begin{eqnarray}
\tan(\theta_y+\theta_z) &=& \frac{\sin(\theta_y+\theta_z)}{\cos(\theta_y+\theta_z)} = -\frac{m_{01}}{m_{00}} \\
\theta_y+\theta_z &=& \arctan(-\frac{m_{01}}{m_{00}})
\end{eqnarray}

となります。

Quaternionを回転行列に変換したとき

\begin{eqnarray}
m_{00} &=& 2q_w^2 + 2q_x^2 - 1 \\
m_{01} &=& 2q_xq_y - 2q_zq_w
\end{eqnarray}

なので

\begin{eqnarray}
\theta_y+\theta_z &=& \arctan(-\frac{2q_xq_y - 2q_zq_w}{2q_w^2 + 2q_x^2 - 1})
\end{eqnarray}

となります。
よって$\theta_x = -\frac{\pi}{2}$ のとき $\theta_y$と$\theta_z$の和が同じであれば同じ回転を表す ことが分かります。

また

\begin{align}
\pi-\frac{\pi}{2} &= \frac{\pi}{2} \\
\pi-(-\frac{\pi}{2}) &= \frac{3\pi}{2} = -\frac{\pi}{2} \\
\pi-\theta_x &= \theta_x & (\theta_x=\frac{\pi}{2},-\frac{\pi}{2}) \\
(\pi+\theta_y)-(\pi+\theta_z) &= \theta_y-\theta_z \\
(\pi+\theta_y)+(\pi+\theta_z) &= 2\pi+\theta_y+\theta_z \\
&= \theta_y+\theta_z
\end{align}

なので ジンバルロック状態でも以下の式が成り立つ ことが分かります。

\boldsymbol{\theta}=(\theta_x,\theta_y,\theta_z) \\
f(\boldsymbol{\theta}) = (\pi-\theta_x,\pi+\theta_y,\pi+\theta_z)

これらをUnityで実装すると以下のようになります。

Vector3 ToEulerAnglesZimbalLock(float x, Quaternion q)
{
    // Z=0radの時のオイラー角を求める
    return ToEulerAnglesZimbalLock(x, 0f, q);
}

Vector3 ToEulerAnglesZimbalLock(float x, float z, Quaternion q)
{
    float y;
    if (x > 0)
    {
        var yMinusZ = Mathf.Atan2(2 * q.x * q.y - 2 * q.z * q.w, 2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.x, 2) - 1);
        y = yMinusZ + z;
    }
    else
    {
        var yPlusZ = Mathf.Atan2(-(2 * q.x * q.y - 2 * q.z * q.w), 2 * Mathf.Pow(q.w, 2) + 2 * Mathf.Pow(q.x, 2) - 1);
        y = yPlusZ - z;
    }

    var angles = new Vector3(x, y, z) * Mathf.Rad2Deg;
    return new Vector3(
        Normalize(angles.x),
        Normalize(angles.y),
        Normalize(angles.z)
    );
}

// 同じ回転を表すオイラー角を取得する
// これはジンバルロック状態の時でも成り立つ
Vector3 GetSameRotationEulerAngles(Vector3 eulerAngles)
{
    // x = 180 - x
    // y = 180 + y
    // z = 180 + z
    return new Vector3(180 - eulerAngles.x, 180 + eulerAngles.y, 180 + eulerAngles.z);
}
28
16
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
28
16