LoginSignup
3
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@y_yoko

モンテカルロ木探索で簡単な数式を解いてみる【日本語翻訳】

Posted at

*本ポストは 先に投稿した英文 の和訳です。

はじめに

こんにちは。Qiitaでのはじめてのポストです。モンテカルロ木探索（Monte Carlo Tree Search: MCTS）を、簡単な数式を解く問題に適用した例をご説明したいと思います。モンテカルロ木探索を、碁とか将棋とかオセロとか以外の問題に、簡単に適用してみたい方もいらっしゃるかと思いますが、本ポストはそういった方々へのものです。またできれば今後、応用例も投稿できればと思っています。

モンテカルロ木探索について

モンテカルロ木探索ですが、コンピューター碁プログラム（AlphaGoなど）で有名になった探索アルゴリズムです。このポストでは、単純な多変数関数を解くことに使ってみたいと思います。

モンテカルロ木探索はルートノードから初めて、次のような４ステップを辿ります。
１．注目ノードの選択
２．注目ノードの子ノード展開
３．適当にサーチ
４．バックプロパゲーション

これに沿って、問題を設定します。

問題の例

例として、次の形の多変数関数の最小値をMCTSによって求めることを考えます。

y = f(x) = (x_1 - a)^2 + (x_2 - b)^2 + (x_3 - c)^2 + (x_4 -d)^2

一般にMCTSを適用したいような問題では、 f(x) の形はよく分からず、アクションに対する報酬としての関係のみが得られるものと考えられますが、ここではf(x)の形から、(x1, x2, x3, x4) = (a, b, c, d)で最小値をとることが分かっています。

MCTSにこの最小値を見つけさせるために、xについての離散的なアクションを次のように定義します。

  • x1 に 1 を加える
  • x1 を 1 減らす
  • x2 に 1 を加える
  • x2 を 1 減らす
  • ...

Xの任意の初期値からスタートし、アクションを繰り返すと、アクションの系列 (x1:+1, x2:-1, ....) となります。MCTSは、アクションの系列に対する累積報酬を最大化するように学習を進めます。

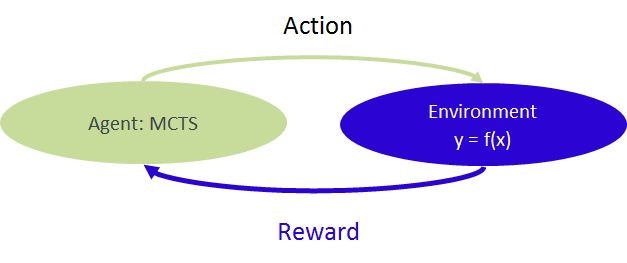
強化学習

解を求めるプロセスを強化学習の形に表現します。この場合 $y=f(x)$ が環境に相当し、MCTSエージェントからアクションを受け取って報酬を返します。

rl.jpg

コードの概略

以下に掲載するコードの主要部分は以下の構造を持ちます。MCTSは確率的であるため、真の最小値にたどり着かない可能性もあります。このためツリーの生成を複数回行い、最小値にたどり着きやすいようにしています。最終的には、最も良い結果が返り値として表示されます。

code_structure.jpg

ソフトウェアのバージョン

  • Python 3.5.2
  • Numpy 1.14.2+mkl

Code


from math import *
from copy import copy

import numpy as np
import random


class environment:
	def __init__(self):
		self.a = 0.
		self.b = 2.
		self.c = 1.
		self.d = 2.
		self.x1 = -12.
		self.x2 = 14.
		self.x3 = -13.
		self.x4 = 9.
		self.f = self.func()
	
	def func(self):
		return (self.x1 - self.a)**2+(self.x2 - self.b)**2+(self.x3 - self.c)**2+(self.x4 - self.d)**2
		
	def step(self, action):
		f_before = self.func()
		
		if action == 1:
			self.x1 += 1.
		elif action == -1:
			self.x1 -= 1.
		elif action ==  2:
			self.x2 += 1.
		elif action == -2:
			self.x2 -= 1.
		elif action ==  3:
			self.x3 += 1.
		elif action == -3:
			self.x3 -= 1.
		elif action == 4:
			self.x4 += 1.
		elif action == -4:
			self.x4 -= 1.
		
		f_after = self.func()
		if f_after == 0:
			reward = 100
			terminal = True
		else:
			reward = 1 if abs(f_before) - abs(f_after) > 0 else -1
			terminal = False
		
		return f_after, reward, terminal, [self.x1, self.x2, self.x3, self.x4]
	
	def action_space(self):
		return [-4, -3, -2, -1, 0, 1, 2, 3, 4]
		
	def sample(self):
		return np.random.choice([-4, -3, -2, -1, 0, 1, 2, 3, 4])

class Node():
	def __init__(self, parent, action):
		self.num_visits = 1
		self.reward = 0.
		self.children = []
		self.parent = parent
		self.action = action
	
	def update(self, reward):
		self.reward += reward
		self.visits += 1
	
	def __repr__(self):
		s="Reward/Visits =  %.1f/%.1f (Child %d)"%(self.reward, self.num_visits, len(self.children))
		return s

def ucb(node):
    return node.reward / node.num_visits + sqrt(log(node.parent.num_visits)/node.num_visits)

def reward_rate(node):
	return node.reward / node.num_visits

SHOW_INTERMEDIATE_RESULTS = False

env = environment()

num_mainloops = 20
max_playout_depth = 5
num_tree_search = 180

best_sum_reward = -inf
best_acdtion_sequence = []
best_f = 0
best_x = []

for _ in range(num_mainloops):
	root = Node(None, None)

	
	for run_no in range(num_tree_search):
		env_copy = copy(env)
		
		terminal = False
		sum_reward = 0
		
		# 1) Selection
		current_node = root
		while len(current_node.children) != 0:
				current_node = max(current_node.children, key = ucb)
				_, reward, terminal, _ = env_copy.step(current_node.action)
				sum_reward += reward
		
		# 2) Expansion
		if not terminal:
			possible_actions = env_copy.action_space()
			current_node.children = [Node(current_node, action) for action in possible_actions]		
		
		# Routine for each children hereafter
		
		for c in current_node.children:
			# 3) Playout
			env_playout = copy(env_copy)
			sum_reward_playout = 0
			action_sequence = []
			
			_, reward, terminal, _ = env_playout.step(c.action)
			sum_reward_playout += reward
			action_sequence.append(c.action)
			
			while not terminal:
				action = env_copy.sample()
				_, reward, terminal, _ = env_playout.step(action)
				sum_reward_playout += reward
				action_sequence.append(action)
				
				if len(action_sequence) > max_playout_depth:
					break
			
			if terminal:
				print("Terminal reached during a playout. #########")
			
			# 4) Backpropagate
			c_ = c
			while c_:
				c_.num_visits +=1
				c_.reward += sum_reward + sum_reward_playout
				c_ = c_.parent
		
	#Decision
	current_node = root
	action_sequence = []
	sum_reward = 0
	env_copy = copy(env)
	
	while len(current_node.children) != 0:
			current_node = max(current_node.children, key = reward_rate)
			action_sequence.append(current_node.action)
	
	for action in action_sequence:
		_, reward, terminal, _ = env_copy.step(action)
		sum_reward += reward
		if terminal:
			break
	
	f, _, _, x = env_copy.step(0)		
	
	if SHOW_INTERMEDIATE_RESULTS == True:
		print("Action sequence: ", str(action_sequence))
		print("Sum_reward: ", str(sum_reward))

		print("f, x (original): ", env.f , str([env.x1, env.x2]))
		print("f, x (after MCT): ", str(f), str(x) )
		print("----------")
	
	if sum_reward > best_sum_reward:
		best_sum_reward = sum_reward
		best_action_sequence = action_sequence
		best_f = f
		best_x = x
	
print("Best Action sequence: ", str(best_action_sequence))
print("Action sequence length: ", str(len(best_action_sequence)))
print("Best Sum_reward: ", str(best_sum_reward))
print("f, x (original): ", env.f , str([env.x1, env.x2, env.x3, env.x4]))
print("f, x (after MCTS): ", str(best_f), str(best_x) )

結果

上のコードを実行すると、MCTSによる最も良いアクションシークエンスが表示されます。
f, x (original) -- 初期状態
f, x (after MCTS) --- アクションシークエンスを実行したときの最期のxとそのときのf(x)

Terminal reached during a playout. #########
Terminal reached during a playout. #########
...
Terminal reached during a playout. #########
Best Action sequence:  [3, -4, -4, 3, 3, 3, -4, -4, 3, 3, 3, -4, -2, -2, -4, -2,
 -2, -4, 0, 3, 1, -3, -2, 1, -4, -4, -3, 3, -1, -2, 3, 1, 1, 4, 1, 4, 2, -2, 1,
-2, 3, -3, 1, 2, -2, -3, 1, 3, -4, -4, -1, -2, -4, 1, 3, -2, 4, 3, 3, 1, -3, -2,
 1, -2, 1, 1, 4, -1, 1, 4, -4, -2, -4, 3, 3, 1, 2, -2, -4, -4, 4, -2, -3, 3, 4,
2, -1, -2, -1, -3, 4, 0, 3, -4, -3, -3, 3, -2, 3, 2, 2, -4, -2, -4, 1, -4, 4, -3
, 1, 3, -1, -2, 4, 3, -4, -1, 2, 4, 2, 1, 4, -4, 4, -3, 1, -1, 4, 0, -3, 2, 1, 4
, 1, -1, 3, 3, -3, -2, 3, 3]
Action sequence length:  140
Best Sum_reward:  141
f, x (original):  533.0 [-12.0, 14.0, -13.0, 9.0]
f, x (after MCTS):  0.0 [0.0, 2.0, 1.0, 2.0]

参考

  1. https://www.youtube.com/watch?v=Fbs4lnGLS8M
  2. https://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search/
  3. https://en.wikipedia.org/wiki/Monte_Carlo_tree_search

補足

上記コードは自由にコピー、修正、利用くださって結構です。本ポストが何かのお役に立ちましたら、引用いただければ幸いです。

3
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?