Introduction
In this my first post on Qiita, I describe Monte Carlo tree search (MCTS) for solving a simple math problem other than Chess, Go, Shogi, etc. This is to see how MCTS works and prepare it for a general application, which is explained in a later post (See also the follow-up post).
Monte-Carlo Tree Search (MCTS)
MCTS is known as an efficient tree search algorithm for computational Go programs. In this post, we see how MCTS can be applied for solving a simple multi-variable equation.
MCTS starts from a root node and repeats a procedure below until it reaches terminal conditions:
- Selection: selects one terminal node using a rule
- Expansion: add additional nodes represents possible actions to a selected node.
- Playout: take random actions from expanded nodes and score values of these nodes based on the outcome of random actions.
- Backpropagation: reflect playout result to all parent nodes up to a root
Example problem
Let's assume a multi-variable equation in the following form and find a minimum using MCTS:
y = f(x) = (x_1 - a)^2 + (x_2 - b)^2 + (x_3 - c)^2 + (x_4 -d)^2
Generally, the form of f(x) is unknown in a type of problems that MCTS would be employed. In this simple example, we already know f(x) take a minimum value at (x1, x2, x3, x4) = (a, b, c, d). We would like MCTS to find a series of actions to reach this minimum. To apply this problem to MCTS, we define discrete actions for x:
- Add x1 to +1
- Add x1 to -1
- Add x2 to +1
- Add x2 to -1
...
etc.
Starting from arbitrary initial values of x and repeating actions, it results in a sequence of actions: (x1:+1, x2:-1, ....). MCTS tries to find an action sequence that maximizes a cumulative reward.
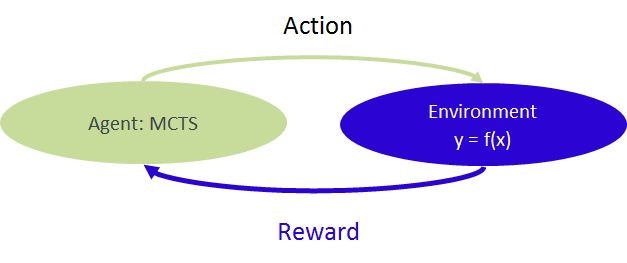
Reinforcement learning
A process to solve the problem can be seen as a reinforcement learning, where the relationship y=f(x) can be seen as "environment" receiving actions from MCTS agent and returning "reward" to MCTS agent.
Pseudo code
The main part of the code has structure below. Since MCTS is probabilistic, it may or may not reach the actual minimum. Thus, a tree is generated multiple times to increase a chance to reach the real minimum and the best result is returned.
Software versions
- Python 3.5.2
- Numpy 1.14.2+mkl
Code
from math import *
from copy import copy
import numpy as np
import random
class environment:
def __init__(self):
self.a = 0.
self.b = 2.
self.c = 1.
self.d = 2.
self.x1 = -12.
self.x2 = 14.
self.x3 = -13.
self.x4 = 9.
self.f = self.func()
def func(self):
return (self.x1 - self.a)**2+(self.x2 - self.b)**2+(self.x3 - self.c)**2+(self.x4 - self.d)**2
def step(self, action):
f_before = self.func()
if action == 1:
self.x1 += 1.
elif action == -1:
self.x1 -= 1.
elif action == 2:
self.x2 += 1.
elif action == -2:
self.x2 -= 1.
elif action == 3:
self.x3 += 1.
elif action == -3:
self.x3 -= 1.
elif action == 4:
self.x4 += 1.
elif action == -4:
self.x4 -= 1.
f_after = self.func()
if f_after == 0:
reward = 100
terminal = True
else:
reward = 1 if abs(f_before) - abs(f_after) > 0 else -1
terminal = False
return f_after, reward, terminal, [self.x1, self.x2, self.x3, self.x4]
def action_space(self):
return [-4, -3, -2, -1, 0, 1, 2, 3, 4]
def sample(self):
return np.random.choice([-4, -3, -2, -1, 0, 1, 2, 3, 4])
class Node():
def __init__(self, parent, action):
self.num_visits = 1
self.reward = 0.
self.children = []
self.parent = parent
self.action = action
def update(self, reward):
self.reward += reward
self.visits += 1
def __repr__(self):
s="Reward/Visits = %.1f/%.1f (Child %d)"%(self.reward, self.num_visits, len(self.children))
return s
def ucb(node):
return node.reward / node.num_visits + sqrt(log(node.parent.num_visits)/node.num_visits)
def reward_rate(node):
return node.reward / node.num_visits
SHOW_INTERMEDIATE_RESULTS = False
env = environment()
num_mainloops = 20
max_playout_depth = 5
num_tree_search = 180
best_sum_reward = -inf
best_acdtion_sequence = []
best_f = 0
best_x = []
for _ in range(num_mainloops):
root = Node(None, None)
for run_no in range(num_tree_search):
env_copy = copy(env)
terminal = False
sum_reward = 0
# 1) Selection
current_node = root
while len(current_node.children) != 0:
current_node = max(current_node.children, key = ucb)
_, reward, terminal, _ = env_copy.step(current_node.action)
sum_reward += reward
# 2) Expansion
if not terminal:
possible_actions = env_copy.action_space()
current_node.children = [Node(current_node, action) for action in possible_actions]
# Routine for each children hereafter
for c in current_node.children:
# 3) Playout
env_playout = copy(env_copy)
sum_reward_playout = 0
action_sequence = []
_, reward, terminal, _ = env_playout.step(c.action)
sum_reward_playout += reward
action_sequence.append(c.action)
while not terminal:
action = env_copy.sample()
_, reward, terminal, _ = env_playout.step(action)
sum_reward_playout += reward
action_sequence.append(action)
if len(action_sequence) > max_playout_depth:
break
if terminal:
print("Terminal reached during a playout. #########")
# 4) Backpropagate
c_ = c
while c_:
c_.num_visits +=1
c_.reward += sum_reward + sum_reward_playout
c_ = c_.parent
#Decision
current_node = root
action_sequence = []
sum_reward = 0
env_copy = copy(env)
while len(current_node.children) != 0:
current_node = max(current_node.children, key = reward_rate)
action_sequence.append(current_node.action)
for action in action_sequence:
_, reward, terminal, _ = env_copy.step(action)
sum_reward += reward
if terminal:
break
f, _, _, x = env_copy.step(0)
if SHOW_INTERMEDIATE_RESULTS == True:
print("Action sequence: ", str(action_sequence))
print("Sum_reward: ", str(sum_reward))
print("f, x (original): ", env.f , str([env.x1, env.x2]))
print("f, x (after MCT): ", str(f), str(x) )
print("----------")
if sum_reward > best_sum_reward:
best_sum_reward = sum_reward
best_action_sequence = action_sequence
best_f = f
best_x = x
print("Best Action sequence: ", str(best_action_sequence))
print("Action sequence length: ", str(len(best_action_sequence)))
print("Best Sum_reward: ", str(best_sum_reward))
print("f, x (original): ", env.f , str([env.x1, env.x2, env.x3, env.x4]))
print("f, x (after MCTS): ", str(best_f), str(best_x) )
Result
Running the code above, it prints the best action sequence found by MCTS
f, x (original) -- corresponds initial state, and
f, x (after MCTS) --- shows final x take all actions and value of f(x).
Terminal reached during a playout. #########
Terminal reached during a playout. #########
...
Terminal reached during a playout. #########
Best Action sequence: [3, -4, -4, 3, 3, 3, -4, -4, 3, 3, 3, -4, -2, -2, -4, -2,
-2, -4, 0, 3, 1, -3, -2, 1, -4, -4, -3, 3, -1, -2, 3, 1, 1, 4, 1, 4, 2, -2, 1,
-2, 3, -3, 1, 2, -2, -3, 1, 3, -4, -4, -1, -2, -4, 1, 3, -2, 4, 3, 3, 1, -3, -2,
1, -2, 1, 1, 4, -1, 1, 4, -4, -2, -4, 3, 3, 1, 2, -2, -4, -4, 4, -2, -3, 3, 4,
2, -1, -2, -1, -3, 4, 0, 3, -4, -3, -3, 3, -2, 3, 2, 2, -4, -2, -4, 1, -4, 4, -3
, 1, 3, -1, -2, 4, 3, -4, -1, 2, 4, 2, 1, 4, -4, 4, -3, 1, -1, 4, 0, -3, 2, 1, 4
, 1, -1, 3, 3, -3, -2, 3, 3]
Action sequence length: 140
Best Sum_reward: 141
f, x (original): 533.0 [-12.0, 14.0, -13.0, 9.0]
f, x (after MCTS): 0.0 [0.0, 2.0, 1.0, 2.0]
References
- https://www.youtube.com/watch?v=Fbs4lnGLS8M
- https://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search/
- https://en.wikipedia.org/wiki/Monte_Carlo_tree_search
Note
This code can be freely copied, modified, and used. Please cite if this post is useful.