この記事は中国のNLP研究者Jianlin Su氏が運営するブログ「科学空間」で掲載された解説記事の日本語訳です。
原文の掲載日は2024/3/18です。
苏剑林. (Mar. 18, 2024). 《时空之章:将Attention视为平方复杂度的RNN 》[Blog post]. Retrieved from https://kexue.fm/archives/10017
近年、線形時間の学習・推論計算量を持つRNNが、少なからずの研究者やユーザーから改めて注目され始めており、どこか「文芸復興」の様相を呈している。その代表作にRWKV、RetNet、Mambaなどが挙げられる。RNNを言語モデルとして使う際の最大の特徴は一回の生成が費やす空間・時間計算量が定数であることだ。系列全体でみると、定数の空間計算量と線形な時間計算量を持つことになる。もちろん、どんな物事にも両面性がある。Attentionが持つ、動的に増大し続けるKV Cacheに比べ、RNNの定数時間な空間計算量は記憶容量に難があり、長いコンテキスト長においてAttentionを上回ることが難しいとされている。
本記事では、Causal AttentionはRNN形式に書き直すことが出来ることを示す。しかも、毎回の生成も$O(1)$の空間計算量で実行できることも示す(かわりに時間計算量が二乗時間を遥かに上回ることになるが)。この事実により、Attentionの優位性は(もしあるとすれば)計算回数の差によるものであり、直感的に考えられているように記憶容量によるものではないことを証明した。AttentionもRNNと同じく、本質的に定数スケールの記憶容量しか持てないものなのだ。
線形RNNを超えて
RNNの支持者はよく、一見反論しがたい主張を持ち出してくる。すなわち、「人間の脳の働きはRNNか、それともAttentionか考えてみればいい」と。
直感的に考えると、RNNの推論の空間計算量は定数である一方、AttentionのKV cacheは動的に増大し続けている。人間の脳の容量に限界があることを考えると、たしかにRNNのほうが脳の働きに近いと言わざるを得ない。しかし、たとえ脳の容量の限界から、人間による1回の推論の空間計算量が定数であると認めたとしても、推論の時間計算量も定数であるとは言い切れないはずだ。あるいは、たとえ1回の時間計算量が定数だとしても、人間が長さ$L$の系列を処理するときは、系列を1回しかスキャンしないとは限らない(「読み返し」みたいなものだ)。なので、合計の推論回数は$L$を大きく上回り、非線形な時間計算量を費やすことになる。
ここで一つ考えてみよう。定数な空間計算量と非線形な時間計算量を持つようにRNNを一般化することで、一般的なRNNが持たない能力(たとえば先ほど挙げた「読み返し」能力)を持たせることはできないだろうか?言語モデルのタスクでは、仮にサンプルは$a,b,c,d,e$だとすると、学習目標は$a,b,c,d$を入力し、$b,c,d,e$を出力することになる。一般的なRNNは下の図のようになる。
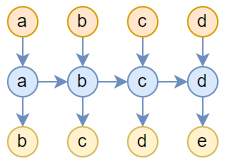
このRNNは「読み返し」をすることができず、入力は一度読み込まれると捨てられる。一方Attentionではトークンが一度読み込まれた後、1回の推論ごとに過去の入力がすべて読み込まれる。このやり方はとても効率的とは言えないが、「読み返し」能力を導入するもっとも単純な方法である。であれば、RNNに「読み返し」能力を持たせるため、Attentionの計算方法を真似てRNNをこう使うことはできないだろうか。
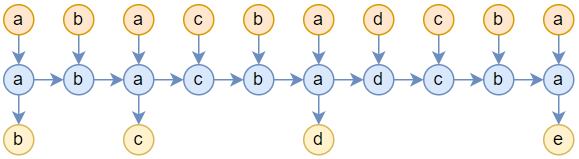
Attentionと同様に、新たなトークンが入力されるごとに、過去の入力を一から読み返すのだ。もちろん、新しいRNNを設計したわけではなく、新しい使い方を考えてみただけだ。入力を改造しただけなので、RWKVやMambaにもそのまま適用できる。この方法では、推論の空間計算量は依然定数だが、時間計算量は線形に増大していき、計算コストは$O(L^2)$になる。
AttentionもRNN
実際、2つ目の図は様々なモデルを表せる。Attentionも一つの特例だと言っていい。
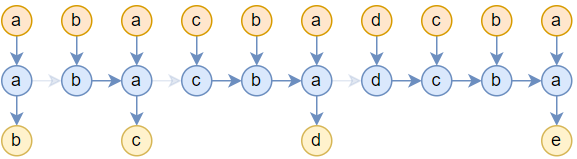
2つ目の図と違い、3つ目の図は一部の矢印が薄くなっているが、Attentionではここの繋がりは切れている。具体的に、Attentionの計算式は:
o_i=\sum_{j=1}^i{a_{i,j}v_j=\frac{\sum_{j=1}^ie^{q_i\cdot k_j}v_j}{\sum_{j=1}^ie^{q_i\cdot k_j}}}\qquad(1)
ここで分子と分母は両方とも再帰的な形式で書くことができる。
\left(
\begin{array}{cc}
y_i^{(t)} \\
z_i^{(t)} \\
\end{array}
\right)
=
\left(
\begin{array}{cc}
y_i^{(t-1)} \\
z_i^{(t-1)} \\
\end{array}
\right)
+e^{q_i\cdot k_{i-t+1}}
\left(
\begin{array}{cc}
v_{i-t+1} \\
1 \\
\end{array}
\right),
o_i=\frac{y_i^{(i)}}{z_i^{(i)}}
\qquad(2)
筆者が読んだ文献の中では、「Self-attention Does Not Need O(n^2) Memory」が初めて上の式にたどり着き、この式でAttention計算の最適化を試みた。また、この式は現在主流の加速技術であるFlash Attentionの理論的な基礎でもある。Self Attentionでは、Q,K,Vは同じ入力からtoken-wiseな計算で得られたものなので、上述の再帰式はちょうど3つ目の図で表せる。
もちろん上の図は1層のAttentionしか描いていない。複数層描くことももちろんできるが、繋がりが少し複雑になる。たとえば2層になるとこうなる。
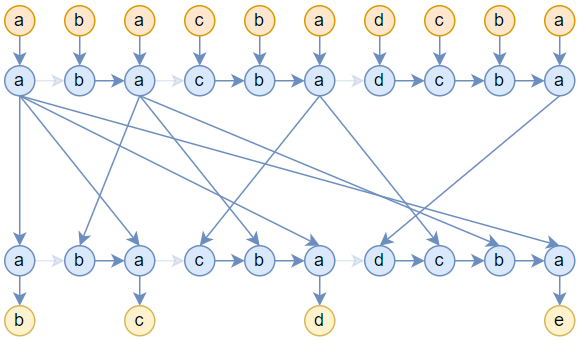
定数空間計算量
冒頭で述べた通り、RNNの主な長所は定数の空間計算量と線形の時間計算量で推論を行うことができることである。AttentionもRNNと見なせるのであれば、同じく以上の長所があるのかどうか、気になるところだ。
まず、Attentionは系列の長さを$O(L^2)$にしたRNNなので、線形な時間計算量は忘れよう。ここで考えたいのは、定数な空間計算量を達成できるかだ。直感的に、それも不可能だと思うかもしれない。周知のとおり、Attentionは線形に増大するKV cacheを持つからである。しかし、これは効率が良い計算方法を採用した、一般的な場合の話である。もしも時間コストを一切鑑みずに空間効率を追い求めれば、空間計算量はどこまで抑えられるのだろうか?
意外に聞こえるかもしれないが、極限まで時間効率を犠牲にすれば、空間計算量を$O(1)$に下げることができるのだ。
実はこれ自体は想像し難くない。まず、上の三つ目の図で表される単層Attentionは、形式的に単層RNNと同一なので、固定サイズのメモリ空間で推論が行えることは明らかである。続いて、四つ目の複数層Attentionでは、層と層の間の繋がりが少し複雑になっている。普通は、過去のK,Vの計算結果をキャッシュすることで効率的な計算を実現しているが、仮に徹底的にキャッシュを行わず、毎回の推論において、すべての層に入力されるK,Vを最初の入力から計算し直すようにすれば、非常に多くの再計算が発生し、時間計算量は二乗スケールを遥かに上回ってしまう。非常にエコじゃない方法だが、空間計算量はたしかに$O(1)$に維持できる。
2層のAttentionを例に考えてみよう。二層目のAttentionは一層目のAttentionの出力を使い、一層目のAttentionの出力は$O(1)$の空間計算量で計算できる。なので効率を犠牲にして再計算すれば、二層目のAttentionも$O(1)$で計算できる。同じように、三層目のAttentionは二層目のAttentionの出力を入力し、$N$層目のAttentionは$N-1$層目のAttentionの出力を入力している。どの層も$O(1)$の空間計算量で計算できるので、モデル全体でも$O(1)$の空間計算量しか費やさないのだ。
これが冒頭の主張に繋がる。もしAttentionがRNNに対して優位性があるとすれば、それはより大きな計算回数によってもたらされたのであって、見かけ上「メモリ」が拡大したのも、時間効率のために空間効率を犠牲したからに過ぎない。本質的に、AttentionはRNNと同じく定数スケールの記憶容量しか持てないモデルである。
「時間効率を犠牲して空間効率を上げるって、別によくある手法ではないか?あまり価値のある結論ではないのでは?」と思った読者もいるだろう。確かにこれはよくある手法だが、常に実現できるわけではないのだ。つまり、どんな問題も時間効率を犠牲にすれば空間計算量を$O(1)$に下げられるとは限らないので、これは非平凡な特性なのだ。
モデル能力の考察
Attentionのこの特性を指摘したのは、本当にこの適性を推論で利用したいのではなく、この結論からAttentionの能力のボトルネックを考察するためである。
まず、極端に厳密さを追求すれば、$O(1)$は本当は間違いで、実際は$O(L)$である。2乗複雑度のRNNは過去の入力を繰り返しスキャンするため、少なくとも入力と出力データは保持する必要がある。つまり$L$個のtoken idを保存する必要があり、保存するための空間は$O(L)$になる。$L$が十分大きければ、$O(L)$は$O(1)$を上回りうる。ここで言う$O(1)$はLLMの前向き計算を行う上で必要なメモリ領域を指している。RNNで言うところのhidden_stateに相当するもので、少なくとも$(hidden\_size\times num\_layers\times2)$個の数値を保存するだけのサイズになる。一方で$O(L)$は入力と出力のサイズを反映している。分かりやすく例えるなら、Attentionは無限大のハードディスクと固定サイズのメモリを持つコンピューターで、コンピューターはハードディスクからデータを読み込み、メモリに保存して計算を行い、またハードディスクに保存する所をイメージしてみてほしい。
皆も心当たりがあると思うが、メモリの容量が大きく、処理するデータ自体は大きくない場面では、私たちは往々にしてプログラミングが「雑」になり、メモリ効率の最適化を二の次にしてしまいがちだ。同じように、「大規模・短系列長」の条件下で学習されたLLMは、系列の長さがもたらす可変サイズの「ハードディスク」よりも、モデルのスケールがもたらす固定サイズの「メモリ」を活かそうとする傾向がある。LLMのスケールが大きく、「メモリ」の容量が十分ある場合、SGDはモデルを無限大の「メモリ」を持つマシンと見なして学習を済ませようとするのだ(系列が短ければ、メモリ容量は常に足りるため)。しかし実際の「メモリ」容量は有限であるため、$O(1)$の空間計算量では実行不可能なタスクに対して、Attentionは任意の長さに一般化することはできない。
$2^x$の十進法表示$y$を計算するタスクを例に考えてみよう。Attentionで条件分布$p(y|x)$を学習するためのデータサンプルは$\{x,[sep],y\}$で、ここでは$y$に対するロスを計算すればいい。$y$は$x$から一意に決まるので、理論上100%の正解率を達成するのは可能なはずだ。しかし、Chain-of-Thought(CoT)のような機構で入力系列の長さを拡大しない限り、モデルは全ての計算過程を非明示的に「メモリ」内で完結させようとする。これは短い入力に対しては有効だが、「メモリ」の容量はどうしても有限である一方、$2^x$の計算に必要な空間は$x$の増大につれて急激に増大していくので、$x$が十分大きければ$p(y|x)$の正解率は必然的に100%を下回る。これは「Transformer進化の旅:16 系列長外挿技術の振り返り」で議論した外挿問題と違い、位置エンコードのOODによるものではなく、CoTによる誘導がない「大規模モデル・短系列」な学習がもたらす欠陥である。
では、なぜ現在のモデル大規模化はCoTみたいな系列長を長くするアプローチよりも、LLMの「メモリ」容量増大、つまりモデルのhidden_sizeやnum_layersを増やすアプローチが主流なのか?前者ももちろん主流研究分野の一つではあるが、「メモリ」の容量のボトルネックはどうしても学習効率と一般性を損なってしまう、というのがある。私たちがプログラムを書く時も、メモリ容量が小さくデータサイズが大きい場合は、計算結果をいちいちハードディスクに書き込んでメモリ空間を確保するように書かざるを得ない。こうなると、アルゴリズムは精緻で難しくなりがちで、具体的なタスクに特化した設計を強いられることもある。
では、「メモリ」のボトルネックはどんな時に起こるのだろうか?LLAMA2-70Bの場合、num_layersは80、hidden_sizeは8192、掛けると約640Kになり、さらに倍にすると約1Mになる。つまり、入力の長さが百万トークン級に達すると、LLAMA2-70Bの「メモリ」はボトルネックになる可能性があるということだ。今のところ、百万トークン級のLLMを学習するのは容易ではないが、手が届かない規模ではない。例えばKimiは百万トークン級のモデルの内部テストを始めている。
「空間計算量が定数である」という結論は、筆者が以前考えていたとある仮説を否定するものでもあった。「モデルのサイズを縮小し、seq_lenを増加させることで大規模モデルと同等の性能を達成できないか?」と考えていたのだが、おそらく無理だろう。小規模モデルの「メモリ容量」ボトルネックを、seq_lenという「ハードディスク」で補うためには、すべての学習サンプルを十分長いCoTで構築する必要があり、これは直接大規模モデルを学習させるよりも困難な作業だ。単純にサンプルをリピートしてseq_lenを水増ししても、新たな情報を含まないので実質的なメリットはない。ただ、prefix tuningによってseq_lenを伸ばす方式であれば、空間計算量の不足を補うことはできるかもしれない。prefixのパラメーターは入力系列からでなく、独立的に学習されたものだからである。例えるなら「外付けメモリ」をいくつも挿しこむようなもので、これによりモデルの「メモリ」を増やしているのである。
時空の旅のおわりに
本記事では、二乗時間RNNの視点からAttentionを考察し、Attentionが定数空間計算量のボトルネックを持つことを示した。この事実から、Attentionは本質的にRNNよりも「メモリ」が大きいわけではなく、ただ計算回数が圧倒的に大きいだけであることが分かった。このボトルネックの存在は、Attentionが特定のタスクにおいて一般化が困難である根本的な原因を示唆している。seq_lenがもたらす「ハードディスク」容量をいかに利用するかが、この問題を解決するカギになるのかもしれない。