ISMIR(International Society of Music Information Retrieval) は、音楽情報処理関連の研究を取り扱う主要な国際学術会議の一つです。今年も11月上旬にサンフランシスコで開催されます。
私も現地に行く予定です。ありがとう弊社。
最先端の研究成果が毎年集まってくるので、本アカウントは毎年いくつかピックアップして紹介しています。
今年も数回に分けて、面白い論文を紹介します。まずは音楽解析(採譜)系です。
Beat this! Accurate beat tracking without DBN postprocessing
音楽ビート・ダウンビート自動推定モデルの提案です。
DNNに基づくビート・ダウンビート推定手法は、一般的に「後処理(postprocessing)」過程を必要としています。DNNは音楽の音響特徴量を入力し、フレームごとに「ビート位置である確率」を出力しますが、DNNの出力確率はノイズが多いため、単にピーク検出しても正確な結果が得られることは稀です。タイトルにもある「DBN postprocessing」は、DNNの出力確率になるべく従う、且つビート・ダウンビートの一般的な法則に従うようなビート・ダウンビート位置を求める、ポピュラーな後処理手法の一つです。
「DBN postprocessing」の具体的な仕組みはともかく、本研究ではこのような後処理は「処理が重い」「楽曲のテンポ変動に柔軟に対応できない」という理由から「後処理無しでも正確なビート・ダウンビート推定ができるDNNを作る」ことを目指しています。
「後処理なし」を実現する手段として、本研究はDNNの構造と損失関数に対する工夫を提案しました。
提案手法:Transformer系のDNN構造
本研究で提案された確率推定用DNNは、Frontend部とTransformer部からなります。Frontend部は入力メルスペクトログラムの周波数軸を2D Conv層で収縮させ、Transformer部がビート確率を推定します。Transformer部は標準的なTransformerブロックの積み重ねで、モデルパラメーターの大半を占める部分です。
Frontend部には2D Conv層だけでなく、時間・周波数軸に交互で注意機構をかけるTransformerブロックを差し込んでいます。
全体的に見て、特にビート推定を利する帰納バイアスを導入する感じでは無さそうですが、とにかく音楽情報処理に有効な工夫を取り入れて強いモデルを組み立てました、という風に見えます。
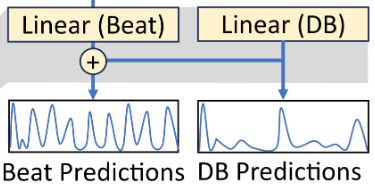
最後の出力層も、ひと工夫入れています。既存の手法では、DNNの出力を全連結層に通して正規化することで、ビート・ダウンビート確率を表す系列に変換します。しかし、ビート・ダウンビート確率を独立的に計算すると(言うほど独立でもないと思いますが)、ビート・ダウンビート位置がたまに一致しなくなる可能性もあります。普通はDBN後処理によって解消されることですが、後処理を無くしたいので何とかしたいです。
そこで、正規化前のビート・ダウンビート確率を足し合わせ、新たなビート確率と見なすという単純な工夫を提案しました。これによって、推定されたダウンビート確率はビート確率にも直接影響するようになるので、位置の不一致が起こりにくくなります。
提案手法:時間ズレに頑健(Shift-torelant)な損失関数
損失関数は、DNNが出力した確率系列と正解ラベルの「距離」を測ります。一般的な手法は各フレームをベルヌーイ分布と見なし、それぞれBCE(Binary Cross Entropy)を計算するだけです。
L_{bce}(y,\hat{y})=-\sum_t\left[y_t\log(\hat{y}_t)+(1-y_t)\log(1-\hat{y}_t)\right]
ただしビート・ダウンビートの性質上、正解ラベル$y=0$の割合が圧倒的に高いので、学習が不均衡になります。損失関数に重み$\omega$を導入することで、不均衡はある程度緩和できるでしょう。
L_{wbce}(y,\hat{y},\omega)=-\sum_t\left[\omega y_t\log(\hat{y}_t)+(1-y_t)\log(1-\hat{y}_t)\right]
それでもまだ問題は残ります。「正解ラベル」と言っても人手によるアノテーションなので、「本当の正解」からズレてたりズレてなかったりします。ズレた正解ラベルで損失を計算すると、本来正しい推定結果が逆に抑制されてしまい、その誤差が積み重なるとDNNの学習が遅くなるうえ、出力確率がビート位置の周辺で「ぼやける」ようになり、ビート位置の特定が難しくなります。
これを解決するために、損失関数計算にmax poolingを加えました。DNN出力確率$\hat{y}$に幅7フレームのmax poolingをかけると、各フレームの値は「その地点の前後3フレーム範囲内の最大値」になるため、正解ラベルが3フレーム以内ズレていても、正しい推定結果が抑制されなくなります。
幅kフレームのmax pooling処理を$m_k(\cdot)$とすると、損失関数は最終的に以下の形になります。
L_{st}(y,\hat{y},\omega)=-\sum_t\left[\omega y_t\log(m_7(\hat{y})_t)+(1-m_{13}(y)_t)\log(1-m_{7}(\hat{y})_t)\right]
DBN無しのビート位置検出
DNNが出力したビート・ダウンビート確率に対し、確率値が0.5を上回った地点でピーク検出を行い、ビート・ダウンビート位置を決めました。また、ダウンビート位置がビート位置とズレている場合、一番近いビート位置に移動させる処理を行っています。
本当に必要最低限の後処理ですね。
実験結果
本研究はビート・ダウンビートラベルを持つ、計18個ものデータセットを集め、8-fold交差検定でビート推定モデルの学習・評価を行いました。ピッチシフトによるデータ拡張もしており、(ビート推定研究にしては)だいぶ大規模な教師ありデータで学習させています。
ベースラインは、現時点でのビート推定SOTAと見なされている(らしい)Transformer系のビート推定モデルです。
ベースラインは「後処理あり」の推定手法ですが、実験結果によると「後処理なし」の提案手法はベースラインをも上回るビート推定正解率を達成しました。ただしベースラインのスコアは、(使ったデータセットが若干異なる)引用元の論文から引っ張ってきた数値なので、そのまま比べるのは若干要注意かも。
とはいえ、後処理抜きでもビート推定能力が凄く高いのは間違いないでしょう。
また、Ablation studiesの結果によると、損失関数の工夫が精度向上に最も貢献したとのこと。この損失関数をそのままベースラインモデルに適用してみたほうが、効果が分かりやすかったかもしれませんね。
"Beat this!"
本研究は実験の再現性を徹底しており、実験コード・学習済みモデル・学習データをすべて公開しています。
そのうえで、論文で「Beat this!」ーーぜひこれを打ち負かして!と呼びかけているのです。ある意味ド直球なスタイルはともかく、先行研究と公平に比較できる実験環境が丁寧に用意されているのは、とても良いことですね。今後どんなチャレンジャーが現れるか楽しみです。
Scoring Time Intervals Using Non-Hierarchical Transformer for Automatic Piano Transcription
DNNとsemi-CRF(semi-Markov Conditional Randam Field)による、ノートレベルのピアノ採譜手法です。Best paper candidateだそうです。
本研究は、同じ著者が提案したピアノ採譜手法に基づいているので、まずはそこから見返す必要があります。
多くの先行研究では、ピアノ採譜問題を定式化する際に音符を「フレーム単位」で定義しているため、推定結果に不自然な「ノイズ」が生じやすい問題に悩まされていました。なので、できれば定式化の時点で音符を「ノート単位」で定義したい。その試みの一つがsemi-CRFによる定式化です。
観測系列$X$にラベル系列$Y$を付ける系列ラベリング問題において、一般的なCRFは以下の式で表されます。
p(Y|X)=\frac{exp[score(Y|X)]}{\sum_{Y'}exp[score(Y'|X)]}
スコア関数$score(Y|X)$は分布である必要はなく、ラベルが正しければ高い値を、間違っていれば低い値を返すような関数です。これを正則化するだけなので、その柔軟な形式から系列ラベリング問題で多く採用されています。
$X$と$Y$の形式、およびスコア関数の計算方法によって色んなタイプのCRFが考えられます。観測系列$X$を複数のセグメントに分割し、セグメントに基づいてラベルのスコアを計算するのが「セミマルコフCRF」です。さっきの定義と比べると、分割方法をあらわす変数$S$が加わります。
P(S,Y|X)=\frac{exp[score(S,Y|X)]}{\sum_{S',Y'}exp[score(S',Y'|X)]}
ピアノ採譜問題をこれに落とし込むと、少々ややこしいですがこんな風になります。
\begin{align}
p(Y_{eventType}|X)&=
\frac{1}{Z(eventType)}exp[\sum_{(i,j,eventType)\in Y_{eventType}}score(i,j,eventType)\\
&+\sum_{[i-1,i]\ not\ covered\ in\ Y_{eventType}}score_\epsilon(i-1,i,eventType)]
\end{align}
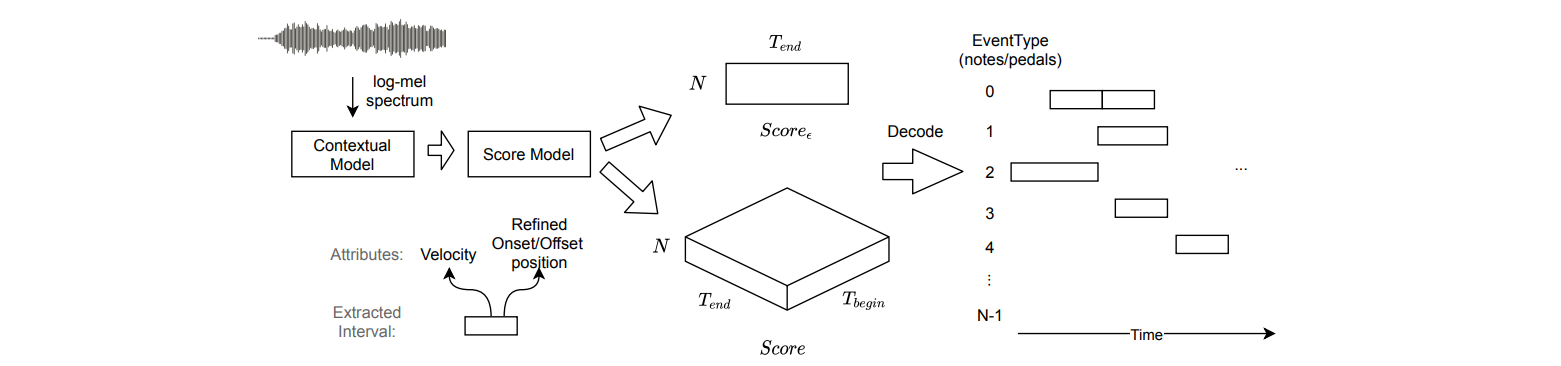
$X$はフレーム単位の音響特徴量(Mel-spectrogramなど)、$Y=\{(i,j,eventType), i\leq j<N\}$はノートイベントの集合($eventType$は音高、$i$と$j$はノートイベントの開始と終了位置)で、$Y_{eventType}$は$Y$の$eventType$を限定した部分集合です。
上の式では、スコア関数を$score(\cdot)$と$score_\epsilon(\cdot)$に分けています。$score(i,j,eventType)$は「位置$i\to j$の$eventType$のノートイベントがある」のスコア、$score_\epsilon(i-1,i,eventType)$は「位置$i-1\to i$はeventTypeのノートイベントに覆われていない」のスコアです。
とにかく、$score(\cdot)$と$score_\epsilon(\cdot)$はそれぞれ3次元・2次元行列で表現できるので、下の図のようにDNNでスコア関数を学習させれば、推定時はスコア行列からViterbiアルゴリズムで最適なイベント列を$eventType$ごとに求め、ピアノ楽譜に変換することができます。
長い前置きになりましたが、ここまでが先行研究(Skipping the ***)の内容です。
提案手法:スコア関数を見直す
本研究の主な貢献は、先行研究で定義したスコア関数を改良することです。
上記の$score(\cdot)$を表すための3次元行列は、入力系列長$N$の2乗に従って増大します。この行列を直接推定しようとすると当然計算量もメモリ消費も爆発します。実際、学習時にはメモリ消費を抑えるためgradient checkpointingなどのテクニックを駆使しており、なかなか扱いが面倒でした。
そもそもスコア関数はほとんどの値が無効な疎行列なので、そんな巨大な行列で表す必要は無いはず。ということで本研究はスコア関数を、以下の形に分解します(以下$eventType$は省略)。
score(i,j)=\frac{|j-i|}{\sqrt{D}}\left<\mathbf{q}_i,\mathbf{k}_j\right>+b_i\delta(i,j)
$\delta(i,j)$は「$i=j$なら$1$、$i\neq j$なら$0$」になる関数(クロネッカーのデルタ)なので、$b_i\in\mathbb{R}$は主体角線の値を表しています。そして$\mathbf{q}_i\in\mathbb{R}^D,\mathbf{k}_j\in\mathbb{R}^D$の内積で$i$から$j$のスコアを表しています。
つまり$score(i,j)\in\mathbb{R}^{N\times N}$は、$\mathbf{q}\in\mathbb{R}^{D\times N}, \mathbf{k}\in\mathbb{R}^{D\times N}, \mathbf{b}\in\mathbb{R}^{N}$に分解できる低ランクな対称行列です($D\ll N$)。$N\times N$な行列を推定する代わりに$\mathbf{q},\mathbf{k},\mathbf{b}$を推定すれば済むなら、だいぶ楽になります。
論文では、ベクトルの次元数$D$がノートの長さの種類数を上回れば、$\mathbf{q},\mathbf{k},\mathbf{b}$で理想的なスコア関数を表現可能なことを理論的に示しています。このルールに従って$D$を決めればOK。
実際のスコア行列計算では、DNNの出力$\mathbf{h}$を線形層$f$に通すことで$\mathbf{q},\mathbf{k},\mathbf{b}$を作ります。すなわち、$[\mathbf{q}_i,\mathbf{k}_i,b_i]=f(\mathbf{h}_i)$。
提案手法:Transformer系の推定器
DNNは長さ$N$のlog-Mel spectrogramを入力し、$eventType$ごとに$\mathbf{h}$を出力します。DNN構造はTransformerに基づいていますが、以下の特徴を持ちます。
- 入力を時間軸でダウンサンプリングし、出力側でアップサンプリングしている(Vision Transformerにインスパイアされたテクニック)
- 入力に加算する位置埋め込みは、Spatial Position Embeddingを採用
- 時間軸と周波数軸(eventType軸)に交互で注意機構をかける(SpecTNTが提案されて以降、最近のTransformer系でよく見る構造…というか上の「Beat this」もそうですね)
実験結果
Maestro、MAPS、SMDデータセットでそれぞれ学習・評価が行われました。
自身のsemi-CRF先行研究はもちろん、より最近提案されたピアノ採譜モデルの評価スコアも上回り、しっかりSOTAを達成しました、ということらしいです。
ベースラインとなったSOTA採譜手法は過去記事で紹介しています。こちらも時間・周波数軸で交互にAttentionするTransformerです。
https://qiita.com/xiao_ming/items/1f96976553e090d24d88#automaticpiano-transcription-with-hierarchical-frequency-time-transformer
ソースコード
この研究も(先行研究と一緒に)提案手法のソースコードが公開されています。
実はsemi-CRFの損失関数計算は(主に$\log Z(eventType)$を求める部分が)少しややこしいのですが、分かりやすいナイーブ実装からテクニカルな高速化実装まで用意されていて参考になります。
このsemi-CRF手法で「作っておぼえる」を書こうとしてたのですが挫折しました。そのうち新しいほうの手法で再挑戦してみるかも。