前提
2020年2月ごろ、金沢大学でとあるニュースが発表されました。
「世界最高精度・最高速度で点群位置合わせ問題の解を見つけるアルゴリズムを発見!」
https://www.kanazawa-u.ac.jp/rd/76252
https://github.com/ohirose/bcpd
Bayesian Coherent Point Drift、という革新的なアルゴリズムを発見したそうです。
このニューズをきっかけにCPDというアルゴリズムについて知りました。
知識のないド素人ですが、せっかくなので
CPD(coherent point drif)について勉強してみようと思います。
英語の翻訳が大変なので完全に個人的なメモ代わりに書いてます。
はじめに
下記記事の続き。
CPD(Coherent Point Drift) ~点群レジストレーション(Point Cloud Registration )~
(1)共通の説明:EMアルゴリズム
https://qiita.com/akaiteto/items/7c563888993272cec72b
(2)非剛体編:損失関数・正規化・事後確率
https://qiita.com/akaiteto/items/87ba9ac8eb5ca440719b
前回はEMアルゴリズムのもとになる対数事後確率の定式化を行いました。
このページでは主にベクトル空間、内積空間、完備距離空間、ヒルベルト空間、ルベーグ空間、再生核ヒルベルト空間等の
数学における空間の概念の概要の復習を行い、RKHS空間の変位関数$v$のノルムについて記載します。
再生核ヒルベルト空間(イメージ編)
本題の前に勉強。
RKHS、再生カーネルヒルベルト空間について。
前提条件などの細かい定義をすっ飛ばしてざっくり勉強します。
(後のほうでは私の理解の範囲で多少細かく記載しました)
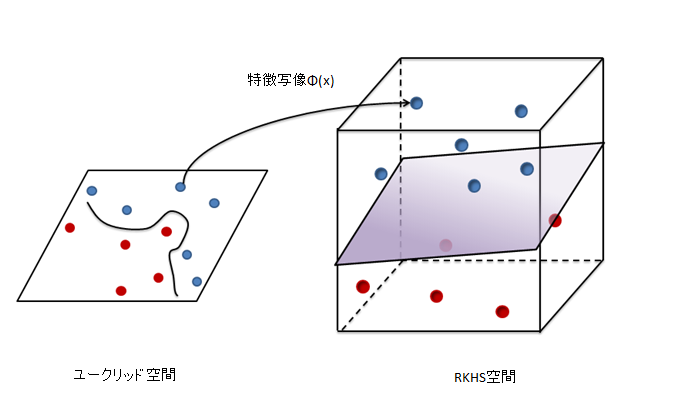
データがぱっと見めちゃくちゃで線形でないデータ$x_{1}$,$x_{2},$...があったとき、
特徴写像$\Phi$を用いてそのデータの次元よりも「高次元の空間」に写像することで、
高次元のデータ$\Phi_{x_{1}}$,$\Phi_{x_{2}}$...$\Phi_{x_{n}}$に変換し、線形性を見出すことで線形的に解析する場合があります。
この「高次元の空間」をヒルベルト空間と呼びます。
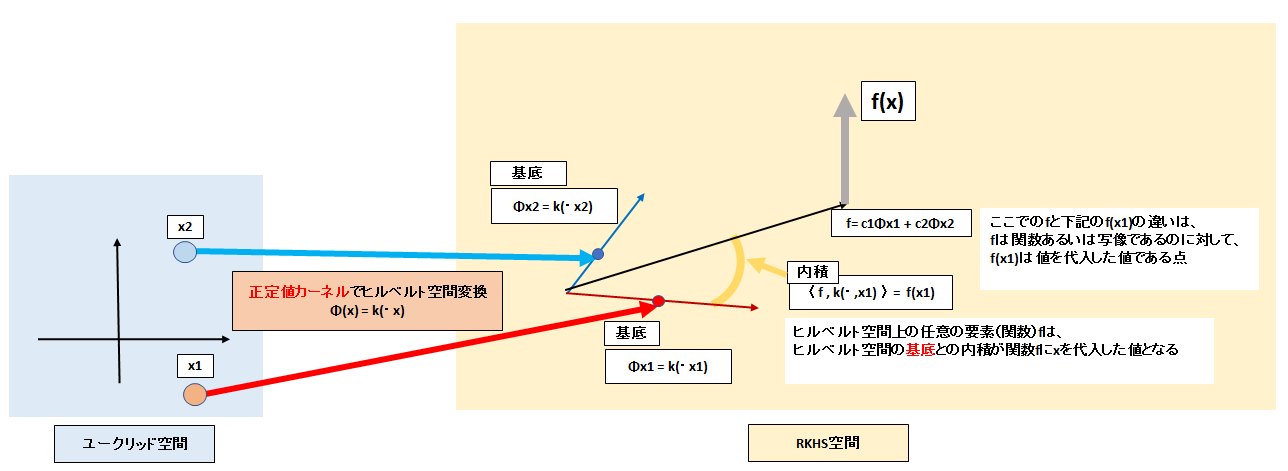
RKHSの各要素$\Phi_{x_{1}}$,$\Phi_{x_{2}}$...$\Phi_{x_{n}}$はカーネル関数$k$と呼ばれるもので表現されます。
「$\cdot$」は変数を表しており、RKHSの要素は関数であり、関数の集合ことを示しています。
\Phi_{x_{1}} = k(\cdot,x_{1})
また、RKHSの空間を表す基底は正定値カーネルと呼ばれるものになります。
基底であるので、RKHSの全ての要素は正定値カーネルによって表現されます。
基底。
たとえば、あるベクトル空間のベクトル$y$は基底$e_{1}$,$e_{2}$があれば
以下のようにあらわされます。(cは定数)
y=c_{1}e_{1}+c_{2}e_{2}
RKHSの空間においても同様に表現されます。
ある要素(関数)$f$は、正定値カーネル$\Phi_{x_{1}}$,$\Phi_{x_{2}}$...$\Phi_{x_{n}}$によって
以下のようにあらわされます。(cは定数)
f=c_{1}\Phi_{x_{1}}+c_{2}\Phi_{x_{2}}+\cdots+c_{n}\Phi_{x_{n}}\\
f=c_{1} k(\cdot,x_{1}) +c_{2}k(\cdot,x_{2})+\cdots+c_{n}k(\cdot,x_{n})\\
f=\sum_{i=1}^{n} c_{i}k(\cdot,x_{i})\\
その他の空間
また脱線復習。
RKHS空間を理解するために、空間という概念について私なりの理解で整理します。
ベクトル空間やユークリッド空間など、空間と呼ばれるものは様々ありますが、
どんな空間も定義しなければ何の性質も発生しません。
距離もノルムも内積も、全ては定義することで初めて利用できます。
以下に、RKHS空間に関連する概念を整理します。
ベクトル空間について。
ベクトルの空間といえば、xyz軸に矢印で2次元なり3次元なりで表現される図を想像できます。
さて、そもそも空間とは集合です。ベクトル空間という集合の原理に立ち返れば、
ある集合$V$に対して、「加法の結合則」「加法の交換則」などの
ベクトル空間の公理を満たす集合が、ベクトル空間です。
ベクトル空間の定義
1.加法の結合律
2.加法の可換律
3.加法単位元の存在
4.加法逆元の存在
5.加法に対するスカラー乗法の分配律
6.体の加法に対するスカラー乗法の分配律
7.体の乗法とスカラー乗法の両立条件
8.スカラー乗法の単位元の存在
言ってしまえば、上記すべての公理を満たすならそれは全てベクトル空間であると見なせる、ということです。
高校数学のベクトル空間は2次元・3次元で表現されましたが、他にもベクトル空間は表現できます。
例えば、見慣れた3次元のベクトルであれば、
以下のような集合で表され、ベクトル空間の定理に一致します。
定理に一致するので下記集合はベクトル空間とみなせます。
\{
{
\left(
\begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}
\right)
}
;
x1,x2,x3∈\mathbb{R}
\}
また、以下のような多項式についても同様に
ベクトル空間の公理を満たすのでベクトル空間とみなせます。
定義にに満たすものであれば、広くベクトル空間としてみなせるということです。
\{a_0+a_1x+\cdots+a_kx^k;a_{i}∈\mathbb{R}\}
内積空間について
これまで当たり前のように内積を使ってきましたが、
これも定義に則って内積が存在するかどうか考えるべきです。
そもそも、その空間では内積は定義できるのでしょう。
内積とは、任意の2つのベクトルの組を実数に映す写像です。
\langle \cdot,\cdot \rangle : V×V \rightarrow \mathbb{R}
このような写像がベクトル空間において下記の内積の定理を満たすとき、
そのベクトル空間は内積空間とみなせます。
内積の定義
1.共軛対称性
2.第一引数に対する線型性
3.正定値性
内積空間を導入することにより、初めてベクトル空間に内積という概念が誕生しました。
内積が定義できない空間は当然ですが内積空間ではありません。内積は存在しない空間となります。
さて、内積の定理をみたす写像であれば、広く内積と定義できます。
内積の例として、n次元のベクトルにおいては以下のような内積の式を立てられます。
\langle \cdot,\cdot \rangle = \sum_{i}^{n} x_{i}y_{i}
見慣れた内積の式です。ちなみにこれを標準内積と呼ぶそうです。
標準内積は内積の定理の条件を満たします。
また、後述しますがヒルベルト空間においては
カーネル関数が内積の定義の一つとして定義できます。
内積と一言でいっても形がいくつもあります。
ノルム空間について
高校数学でノルムというと、$\sqrt{x_{1}^{2}+\cdots +x_{2}^{2}}$のような式を思い出します。
このノルムにも明確な定義があり、その定義を満たすものは全てノルムであると言えます。
ノルムの定義としてはあるベクトル空間Vに対して、実数を映し出す写像です。
\|\cdot\|:V \rightarrow \mathbb{R}
このような写像がベクトル空間においてノルムの定理を満たすとき、
そのベクトル空間はノルム空間とみなせます。
ノルムの定義
1.半正値性
2.斉次性
3.三角不等式
内積空間とノルム空間について
ノルム空間の項で述べた通り、ノルムの定義を満たす写像がベクトル空間において定義されれば、
その空間はノルム空間とみなすことができ、ノルムを使うことができるようになります。
ここで、内積空間をなすとあるベクトル空間$V$があったとします。
このとき、実は内積の式からノルムの定義を満たすノルム$|\cdot|$を、自然と見出すことができます。
\|v\|=\sqrt{\langle v,v \rangle}
これにより、内積とノルムを組み合わせた性質を内積空間に見出すことができます。特別な定義等はいりません。
このことから内積空間はノルム空間でもあると言えます。
内積空間とノルム空間が結びついたことで、様々な性質を見出すことができます。
内積空間を満たすベクトル空間$V$の要素$u$,$v$として、参考までにいくつかの性質を記載します。
(1)コーシー=シュワルツの不等式
|\langle u,v \rangle| \leq \|u\|\cdot\|v\|
以前内積の例の一つとしてn次元ベクトル空間の内積を示しました。
\langle \cdot,\cdot \rangle = \sum_{i}^{n} x_{i}y_{i}
シュワルツの不等式より、以下のような別の形式の内積をも見出すことができます。
\langle u,v \rangle = \|u\|\|v\|cos\theta
この式もまた内積の定義を満たすので内積とみなされます。
内積の定義を満たせば内積の式になり得ることの例としてここでは提示しました。
また、この式により内積空間に「角度」の概念が導入されます。
(2)三角不等式
|\langle u,v \rangle| \leq \|u\|+\|v\|
完備距離空間
まっさらな何もない空間における距離を考えたとき、
距離とはそもそもなんであるかを定義しないと距離は測れません。
数学においては距離の定義が存在します。
任意の集合Xにたいして、距離の公理を満たす距離関数が定義される空間を距離空間と呼びます。
良く知られる例として、ユークリッド空間は距離空間の一種です。
二次元ユークリッド空間で距離を測るときは以下のような距離関数が持ちいられます。
中学数学で学んだ「二点間の距離の公式」です。
d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}
このように距離関数を定義できる空間を距離空間といます。
また、「完備」である距離空間を完備距離空間といいます。
コーシー列とは、十分先のほうでほとんど変化しなくなる数列のことを言い、
完備であるとは、定義的には空間Mの任意のコーシー列が収束することをいいます。
コーシー列、完備という単語の意味について勉強します。
https://rikei-jouhou.com/cauchy-sequence/
その前に数列の収束について。
∀ε > 0, ∃N\geq1 , ∀n ∈ N |s_{n}-s|<ε
が成り立つとき、数列はsに収束するという。
\lim_{n \to \infty} s_{n} = s
上記のように、ある数列$s_{n}$が収束することを示すには、
極限$s$をあらかじめ知っておく必要があります。
極限を知らずとも数列が収束するか確認するアイディアがコーシー列です。
定義としては以下の定義をみたす数列$s_{n}$はコーシー列となります。
∀ε > 0, ∃N\geq 1 , ∀n ∈ N ,∀k\geq 1,|s_{n}-s_{n+k}|<ε
コーシー列が収束することを完備であるといいます。
直観的な言葉としては、
「完備性を持つ空間は」
「隙間が埋まっている空間」
「点を追いかけても空間からはみ出ない」といいます。
ヒルベルト空間
「完備性」と呼ばれる性質を備えた内積空間を、特別にヒルベルト空間と呼びます。
https://www.slideserve.com/foy/2
内積空間であるので、内積とノルムを持ちます。
加えて、ヒルベルト空間は完備距離空間でもあります。
一般に、内積空間の多くは完備ですが、
無限次元の内積空間は完備ではない場合があります。
ヒルベルト空間では、有限次元無限次元どちらも扱えますが、
無限次元の内積空間の中でも特に完備性を持つ空間とも言えます。
L2空間 = ヒルベルト空間
関数が要素となるベクトル空間を関数空間といいます。
ここでは、関数空間の一つである$L^{p}$空間のうちの$L2$空間について触れます。
\|f\| = \left(
\int_{S} |f(x)|^{p}dx
\right)^{\frac{1}{p}}
上式のように定義できる関数$f$の集合をL^{p}空間と呼び、
\|f\| = \left(
\int_{S} |f(x)|^{2}dx
\right)^{\frac{1}{2}}
$p=2$の場合をL2空間と呼びます。
これらは必ず$|f|<\infty$を満たし、有界となります。
\|f\| = \left(
\int_{S} |f(x)|^{p}dx
\right)^{\frac{1}{p}} < \infty
L2空間に属する関数の一例としては、
$f(x)=e^{-ax}$はp=2において$|f|<\infty$を満たすのでL2空間に属する関数と言えます。
また、l=2におけるこのような関数を自乗可積分函数と言います。
さて、これらの式はノルムであるのでノルム空間ともみなせます。
$(f+g)=f(x)+g(x)$
$λf(x)=f(λx)$
また、関数でありながら上記のようなベクトルの定義を適用できるので、ベクトル空間ともみなせます。
\langle f,g\rangle _{H}=
\int_{S} f(x)\overline{g(x)}dx
また、L2空間は上式のように内積を定義できるので内積空間でもあります。
d_{p}(f,g)=\|f-g\|^{p}\\
d_{2}(f,g)=\|f-g\|^{2}
また、距離関数も上式のように定義できます。
さらに、実はこの距離空間は完備性も備えています。
以上より、L2空間は完備な内積空間とみなせるので、
L2空間はヒルベルト空間とみなせます。
ちなみに余談なので詳細は省きますが、L2空間はヒルベルト空間ではありますが
下記に記載する再生核ヒルベルト空間にはなりません。
再生核ヒルベルト空間
再生性の条件
https://people.eecs.berkeley.edu/~bartlett/courses/281b-sp08/7.pdf
ヒルベルト空間は内積空間です。内積空間なので内積が定義できます。
\langle x,y \rangle = \sum_{i}^{n} x_{i}y_{i}
ヒルベルト空間における内積としては、見慣れた上式のほかに
カーネル関数でも表現することができます。
\langle x,y \rangle = k(x,y)
さてここで、以下のようなヒルベルト空間を考えます。
もとのデータの集合$Ω$より、写像$Φ:Ω→H$によって移されたときの
関数を要素に持つヒルベルト空間(関数空間)について考えます。
ある要素$x∈Ω$が$\Phi_{x}$でヒルベルト空間に移されたとき、
ヒルベルト空間の任意の要素(関数$f$)に対して、以下の性質が成り立つとする。
\langle f,\Phi_{x}\rangle = f(x)
この条件が成立するヒルベルト空間を再生核ヒルベルト空間RKHSといいます。
上式を一般に再生性の条件と呼びます。
また、特徴写像$\Phi_{x}$について、
\Phi_{x}=k(\cdot,x)
上式のようにカーネル関数で置けたとき、このカーネル関数$k(\cdot,x)$を再生核と呼びます。
よって先ほどの再生性の条件の式は以下のようにあらわされます。
\langle f,k(\cdot,x)\rangle = f(x)
また、このようなカーネル関数は、以下の性質を持ちます。
1.対称性
k(x,y)=k(y,x)
2.正定性
\sum_{j,i=1}^{n}c_{i}c_{j}k(x_{i},x_{j}) \geq 0
このようなカーネル関数を正定値カーネルと呼びます。
次に、RKHSの各要素について考えます。
RKHSは関数空間です。要素として関数$f$を持ちます。
$f$は関数なので、要素$x$を与えれば$f(x)$として値を持ちます。
このとき、$f(x)$はどのような値になるでしょうか。
このような関係を汎関数として写像で表せば、
$L_{x}:f→f(x) ; ∀f∈H$
と表されます。
リースの表現定理より、
L_{x}(f)=\langle f,k(\cdot,x)\rangle
と表される$L_{x}(f)$は必ず有界となります。
$L_{x}(f)$は上記の汎関数の写像であるのでしたがって、
\langle f,k(\cdot,x)\rangle = f(x)
となり、先ほど提示した再生性の証明につながります。
Moore-Aronszajn の定理
さて、ここまでの話だと、再生核ヒルベルト空間が
実際にどのような空間化イメージしづらいかもしれません。
Moore-Aronszajn の定理を考えることで、
以下の3つの性質をもつ再生核ヒルベルト空間を見出すことができます。
k(x,y)が正定値カーネルとすると
1.$k(\cdot,x)∈H$
2.$f=\sum_{i}c_{i}k(\cdot,x_{i})$
3.再生性の条件を満たす
RKHS空間は完備な内積空間なので、ベクトル空間です。
1より、カーネル関数$k(\cdot,x)∈H$を基底として持ち、
2より、基底でもって任意のベクトル$f$が表現される、そういうベクトル空間となります。
また、関数空間でもあるのでこれらの要素は関数です。
再生性の条件により、関数は有界となります。
関数の値は無限ではなく有限であるということです。
カーネルトリック
また、Moore-Aronszajnの定理により、別の性質も見出すことができます。
このRKHS空間に対して、ある要素(関数)である$f,g$の内積を計算してみます。
2より各要素の式を適用すると、
\langle f,g\rangle =\langle \sum_{i}a_{i}k(\cdot,x_{i}),\sum_{j}b_{j}k(\cdot,x_{j}) \rangle
\langle f,g\rangle =\langle \sum_{i}\sum_{j}a_{i}b_{j}\langle k(\cdot,x_{i}),k(\cdot,x_{j}) \rangle
そして再生性の条件より、以下の式が成立する。
\langle k(\cdot,x),k(\cdot,y)\rangle = \langle Φ(x),Φ(y)\rangle = k(x,y)
これをカーネルトリックといいます。
カーネルトリックによるリッジ回帰・正規化項
カーネルトリックにより、ヒルベルト空間で内積の計算をおこなおうと思った場合には、
カーネル関数で簡単に計算することが可能になります。
ヒルベルト空間の項でも記載した通り、
ヒルベルト空間は無限次元の関数空間でもあります。
無限次元空間はいかにも計算的に困難が発生しそうな空間ですが、
正則化の考えを導入することで有限次元として考えることができます。
実際の例として、CPDにも関係のあるリッジ回帰を元に勉強します。
\min_{\tau∈H,x,y∈R^{n}} =
\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + λ|w|^{2}\\
正規化理論で述べたものとほぼ同じものを考えます。
データ$x,y∈R$が存在し、二乗誤差を最小とする関数$\tau$を求めるリッジ回帰の問題です。
このとき、$\tau$をRKHSに含まれる要素(関数)であるとみなします。
\langle f,k(\Phi_{x},x)\rangle = f(x)
\langle f,k(\cdot,x)\rangle = f(x)
\langle \tau,k(\Phi_{y_{i}},y_{i})\rangle = \tau(y_{i})
再生性の条件より、リッジ回帰の式は以下のようになります。
\min_{\tau∈H,x,y∈R^{n}} =
\sum_{i=1}^{l}[x_{i}-
\langle \tau,k(\Phi_{y_{i}},y_{i})\rangle
]^{2} + λ|w|^{2}\\
このとき、ヒルベルト空間は無限次元であるので問題は困難ですが
リプリゼンター定理を導入することで単純な形式で解を示せます。
結論から言えば、最適な$\tau$は
\tau = \sum_{i=1}^{l}a_{i}k(\cdot)k(\cdot,l)
のように、$l$個の線形結合で最適な$\tau$が表されます。
これにより、リッジ回帰のカーネル化ができました。
正規化理論 その2
脱線しまくりましたが本題に戻ります。
以前の投稿では、$Φ(v)$や変位関数$v$が不明なので定式化しなければならないことについて触れました。
R[v]=R_{emp}[v] + λR_{reg}[v]\\
R[v]=\frac{1}{2}\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + \frac{1}{2}λ|Dv|^{2}\\
さて、$R[v]$は以前述べた通り$v$に関する汎関数です。
RKHSの項でリッジ回帰について記載しましたが、
上式はリッジ回帰と同じような式であることがわかります。
$R[v]$も同様に、$\tau∈H$、$x,y∈R$であるとみなします。
したがって、ノルム$|v|$をRKHSのL2ノルムとなります。
$|v|$はどのような式でしょうか。
RKHS空間はノルム空間でもあるのでノルムは定義できるはずです。
Lp空間に基づくp-ノルムなどさまざまなノルムの定義がありますが、
[On Different Facets of Regularization Theory p2800]によれば、
$v$をRKHS空間のノルムは下記式で定式化することができるそうです。
|v|_{H}^{2} = \int_{R^{D}}\frac{|V(s)|^{2}}{K(s)}ds
$D$は参照する点群のポイントの数、
$V(s)$は関数$v$のフーリエ変換、
$K(s)$はカーネル関数$k$をフーリエ変換したものです。
カーネル関数はどれがよい?変位関数はどんな式?
個の式だけでは情報が足りません。
[Regularization theory and neural networks architectures]
https://www.researchgate.net/publication/2246342_Regularization_Theory_and_Neural_Networks_Architectures
上記の論文曰く、滑らかな関数とは「振動」が少ない場合のことを言うらしいです。
それに従えば大きな振動、すなわち高周波成分を除去された関数は、滑らかであるとみなせます。
フーリエ変換といえば周波数領域。
次回はそのあたりの掘り下げを行います。