前提
2020年2月ごろ、金沢大学でとあるニュースが発表されました。
「世界最高精度・最高速度で点群位置合わせ問題の解を見つけるアルゴリズムを発見!」
https://www.kanazawa-u.ac.jp/rd/76252
https://github.com/ohirose/bcpd
Bayesian Coherent Point Drift、という革新的なアルゴリズムを発見したそうです。
このニューズをきっかけにCPDというアルゴリズムについて知りました。
知識のないド素人ですが、せっかくなので
CPD(coherent point drif)について勉強してみようと思います。
英語の翻訳が大変なので完全に個人的なメモ代わりに書いてます。
はじめに
下記記事の続き。
CPD(Coherent Point Drift) ~点群レジストレーション(Point Cloud Registration )~
(1)共通の説明:EMアルゴリズム
https://qiita.com/akaiteto/items/7c563888993272cec72b
前回はCPDにおける対数尤度関数とQ関数の定式化を行いました。
このページでは、非剛体の位置合わせの理論の基礎の部分、
正規化項を考慮したリスク汎関数の定式化と、
非剛体の位置合わせを想定した場合の事後確率について記載します。
位置合わせの変換式
あるポイント$X$と、別のポイント$Y$があったとします。
それぞれの点群のポイント数が異なり、以下のようなポイントの集合をもっています。
X=(x_{1} \cdots x_{N}) \\
Y=(y_{1} \cdots y_{M}) \\
$Y$のポイントはGMMの重心、$X$のポイントはGMMによって生成されたデータとみなします。
剛体において、点群$Y$の位置を調整して点群$X$に重ねようとした場合、
回転行列$R$、移動行列$t$、大きさのスケール$s$とすると、
点群$X$に位置合わせを行った点群$Y'$は以下の式で表されます。
Y' = \tau(Y;R,t)=sRY+t
上式により、剛体の点群は画像のように位置合わせが行われます。
一方非剛体の場合、形状がかわるので同じような式で位置合わせを行うことができません。
それぞれのポイントに対する変位を変位関数$v$とすると、
点群$Yに対して$位置合わせを行った点群$Y'$は下記式で表されます。
Y'=\tau(Y)=Y+v(Y)
このように変形して行われる位置合わせは、画像のように各点がそれぞれ移動して変形します。
このときの性質は以下のようになることが想像できます。
・ポイントが近い場合、それらのポイントは同じ物体である。
・ポイントが近い場合、それらのポイントの動きは同じ動きをする。
このような動きを伴う移動体には、
モーションコヒーレント理論(motion coherence theory:MCT)を導入することができます。
[A mathematical analysis of the motion coherence theory]
https://www.researchgate.net/publication/220659762_A_mathematical_analysis_of_the_motion_coherence_theory
CPDにおいては、このMCT理論が1つの重要な理論となります。
MCT理論を適用することでとある式を導出できるのですが、
論文の「2 The Theory」によると、変位関数$v$はできるだけ「滑らか」である必要があります。
したがって、MCT理論を適用する前に変位関数$v$を滑らかにする理論の導入が必要です。
正規化理論
変位関数vを滑らかにするにはどうすればよいか。そこで用いられるのが正規化理論です。
[On Different Facets of Regularization Theory]p2796
https://www.researchgate.net/publication/10985698_On_Different_Facets_of_Regularization_Theory
[Regularization theory and neural networks architectures]
https://www.researchgate.net/publication/2246342_Regularization_Theory_and_Neural_Networks_Architectures
(参考:https://www.hellocybernetics.tech/entry/2019/10/29/070640)
$\tau$についてもう少し考えてみます。
例えば、ある$f(x)$が実数xによって決定される実関数であるなら、
$\tau$は変位関数$v$の値によって決定される関数、関数の関数、すなわち汎関数です。
\tau(v)=Y+v(Y)
$\tau$は点群$X$に対して位置合わせを行った後の点群でした。
メインの点群とターゲットの点群、Xと位置合わせ後の点群の二乗誤差は以下のようになります。
R_{emp}=\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2}
$R_{emp}$は機械学習で言うところの損失関数、リスク関数と呼ばれるものに近いものです。
通常のリスク関数で有れば$\tau$の最適化を行いますが、$\tau$は上述の通り変位関数$v$を内部にもつ汎関数。
R_{emp}[v]=\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2}
したがって、$R_{emp}[v]$も同様に汎関数であると言えます。これを損失汎関数と呼びます。
よくある損失関数は二乗誤差の内部に定義された関数$\tau$にたいして最適化が行われますが、
リスク汎関数では$v$と$\tau$も考慮する必要が発生します。
さて、もう一度式を見ます。
理想的な測定が行えていれば、Σでくくられた誤差の総和は0になるはずです。
しかし、データに含まれるノイズや外れ値の影響で厳密に誤差が0になることはまずありえません。
参照するポイントが増えるほど、理想的な$\tau$の再現度が上がりますが、
それと同時に増えたポイントから受けるノイズの影響も強くなります。
そして最終的には$\tau$の関数は誤った結果となってしまうでしょう。
R[v]=R_{emp}[v] + λR_{reg}[v]\\
R[v]=\frac{1}{2}\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + \frac{1}{2}λ|Dv|^{2}\\
R[v]=\frac{1}{2}\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + \frac{1}{2}λ\|w\|^{2} \tag{1}
そこで、正規化理論では「正規化項」を加えます。
機械学習で言うところの過学習対策と同様に、Tikhonov正規化によって
$\tau$に関する損失関数は以下のように定式化されます。
名称としては、経験的リスク汎関数$R_{emp}[f]$と正則化リスク汎関数$R_{reg}[f]$と呼びます。
以下に、初出の変数について見てみます。
●λ
$λ$は、正規化項の強さを表す係数です。上述の通り、ポイント数が増えるほどに$\tau$はノイズの影響を受けてしまいます。
正規化項はポイントの数に応じて値が大きくなる項であり、ポイント数がおおいほど、正規化項を大きくしてノイズの影響を減らすように働きます。
●D
$D$はフレシェ微分。(メモ:重要そうだったらあとでふかぼりする)
XをYにマッピングする関数は、Xのあるポイントxでフレシェ微分可能であるというらしいです。(論文p2797)
ここでは一旦、$Df$を$w$としておく。
●|・|
ヒルベルト空間のノルムを指します。(ヒルベルト空間については後のほうで触れます。)
(1)の式は、平滑化スプラインの式と一致します。
$λ$はノイズの調整と同時に、$v$の曲線としての滑らかさを調整する役割を持っています。
CPDでは平滑化スプラインの効果でも平滑化が行われますが、
他の要因でも平滑化が期待されます。(後述)
MAP推定とEMアルゴリズム
以前の投稿では対数尤度関数に対してEMアルゴリズムの式を立てました。
https://qiita.com/akaiteto/items/7c563888993272cec72b
剛体においては、対数尤度関数に対してEMアルゴリズムを行うのですが、
非剛体においては、尤度ではなく事後確率を求めることでEMアルゴリズムを適用させます。
以下に詳しく見ていきます。
まず、復習がてら確率の式を確認します。以降では$D$をデータ、$m$をパラメータとします。
同時確率$p(x,y)$について。
乗法定理より以下の式が成立します。
p(x,y)=p(y|x)p(x)
事後確率$p(m|D)$について。
ベイズの定理より、事後確率は以下のように定義されます。
p(m|D)=\frac{p(D|m)p(m)}{p(D)}
$p(D|m)$は尤度、$p(m)$は事前確率、$p(D)$は周辺尤度です。
ここで、データDを$m_{1}$...$m_{M}$に分割したものとみなした時、
$m_{i}$の事象が互いに独立であるとすれば、事後確率$p(m|D)$は以下のように展開されます。
p(m|D)=\frac{p(D|m)p(m)}{\sum_{i=0}p(D,m_{i})}\\
p(m|D)=\frac{p(D|m)p(m)}{\sum_{i=0}p(D|m_{i})p(m_{i})}\\
これを図にすると以下のようなイメージです。
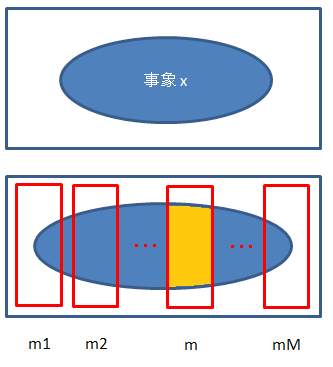
分母の$p(D)$は、分子を要素にした全体の確率、また$p(D)$は事後確率の全積分が1にする役割として存在します。
さて、事後確率のパラメータ$m$を最大化させる問題としてみなした時、
$p(D)$にはパラメータ$m$に依存しないので、$p(D)$は定数とみなすことができます。
このことをを式にすると
p(m|D)∝p(D|m)p(m)\\
p(m|D)=kp(D|m)p(m)
$k$を正規化定数、$p(D|m)p(m)$をカーネルとも呼びます。
ここまでが一般形の話。
この事後確率の式に正規化理論を導入します。
(p2819 On Different Facets of Regularization Theory )
正規化理論では、事前確率を以下のように定義します。
p(m) = \frac{exp(-λR_{reg}(m))}{\int exp(-λR_{reg}(m))dw}\\
p(m) = \frac{exp(-λR_{reg}(m))}{Z_{m}(λ)}
$λ$と$R_{reg}(m)$の選択は、$p(m)$をどう仮定するかに依存します。
ここでは、事前分布$p(m)$を以下のように仮定します。
p(m)=exp(-\frac{λ}{2}\|w\|^{2}) \tag{3}
(3)を、ベイズの定理で表された対数事後確率に代入します。
\log p(m|D) = \log \frac{p(D|m)p(m)}{p(D)}\\
\log p(m|D) = \log p(D|m) + \log p(m) - \log p(D)\\
\log p(m|D) = \log p(D|m) -\frac{λ}{2}\|w\|^{2} - \log p(D)
上述の通り、周辺尤度$p(D)$は定数とみなせるので、
式は以下のように展開されます。
\log p(m|D) = \log p(D|m) -\frac{λ}{2}\|w\|^{2}
ここで、論文の定義に立ち返ります。
$m$は点群$Y$の各ポイントのインデックス、
$D$は位置合わせのターゲットとなる点群$X$のポイント$x$とすると、
以下のようになります。
\log p(m|x) = \log p(x|m) -\frac{λ}{2}\|w\|^{2} \tag{3}
$p(x|m)$は尤度関数です。
以前の投稿では、尤度関数$p(x|m)$は以下のような式になりました。
\log p(x|m)=\sum_{n=1}^{N}log\ \sum_{m=1}^{M}P(M+1)p(x|m)\\
最尤推定においては、対数尤度関数$\log p(x|m)$を最大化するパラメータ$m$が求められます。
論文の記載に合わせて、負の対数尤度関数として以下のように定義します。
E=-\sum_{n=1}^{N}log\ \sum_{m=1}^{M}P(M+1)p(x|m)\\
マイナスがついたことで、この問題は
最小化するパラメータを発見する問題に置き換わります。
これを(3)に代入します。
$|w|^{2}$を$Φ(v)$として式を整理します。
\log p(m|x) = -E -\frac{λ}{2}\|w\|^{2} \\
-\log p(m|x) = E +\frac{λ}{2}\|w\|^{2} \\
f = E +\frac{λ}{2}Φ(v) \tag{4}
これにより、対数事後確率が式にできました。
マイナスがついているので、最小化することで最適化を行います。
Φ(v)について
次はQ関数を求めてEMアルゴリズムを実行・・・の前に、変位関数$v$について掘り下げます。
(4)では、$|w|^{2}$を$\Phi(v)$とおきました。ですが$|w|^{2}$に$v$は含まれていません。
$\Phi(v)$の$v$は上述の(1)に由来されます。
R[v]=R_{emp}[v] + λR_{reg}[v]\\
R[v]=\frac{1}{2}\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + \frac{1}{2}λ|Dv|^{2}\\
R[v]=\frac{1}{2}\sum_{i=1}^{l}[x_{i}-\tau(y_{i})]^{2} + \frac{1}{2}λ\|w\|^{2} \tag{1}
[On Different Facets of Regularization Theory]p2796
https://www.researchgate.net/publication/10985698_On_Different_Facets_of_Regularization_Theory
次回以降
上式より、$\Phi(v)$は$\Phi(v)=|w|^{2}=|Dv|^{2}$となり、
$\Phi(v)$が$v$のノルムにかかわる式であることがわかります。
以上より、事後確率に対するEMアルゴリズムの準備が多少整いましたが、
Φ(v)の式は何であるか、vとは何かについては不明なままです。
次回以降で勉強します。

