逆動力学計算を完全に理解しましょう！

なかなか自分の口に合う導出がないので、梶田さんの教科書とchoreonoidのソースコード読んで自分なりに整理した(わかりやすさ重視)。またこの文書の各フォントの意味合いが以下の通り：

• $i$: 変数、スカラー
• $\boldsymbol i$: ベクトル
• $\bf i$: 行列

説明する内容

ロボットをこう運動させるとき(時系列関節角度既知)に各関節がどれくらいのトルク(時系列トルク未知)を出せばいいのかの計算。また逆動力学の計算にはラグランジュ方程式に基づく計算法とニュートン・オイラー方程式に基づく計算法２つがある。この文書は計算量の少ないニュートン・オイラー法を解説する。

空間速度

ワールド座標系から見た剛体上の点 ${\boldsymbol p}$ 、この点の並進速度を ${\boldsymbol v}$ 、角速度を ${\boldsymbol w}$ で表す。
この剛体の空間速度 ${\boldsymbol v}_o$ は以下の式で定義する。

{\boldsymbol v}_o = {\boldsymbol v} - {\boldsymbol w} \times {\boldsymbol p} \tag{1}

空間速度の微分 $\dot{{\boldsymbol v}}_o$ は以下の式で計算する。

\dot{{\boldsymbol v}}_o = \dot{{\boldsymbol v}} - \dot{{\boldsymbol w}} \times {\boldsymbol p} - {\boldsymbol w} \times {\boldsymbol v} \tag{2}

加速度まで考慮する順運動学計算(リンクの速度、角速度、速度微分、角速度微分の計算)

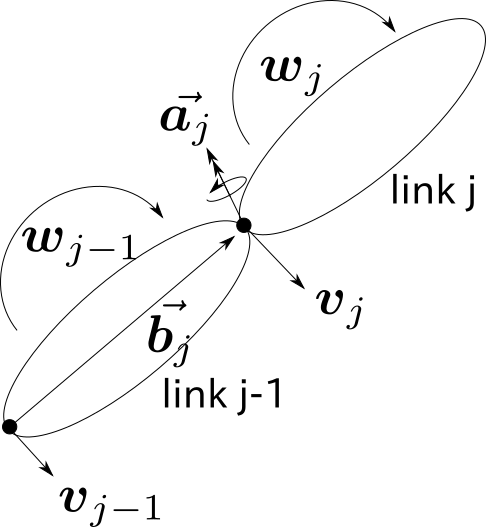
リンク $j$ の角速度${\boldsymbol w_j}$と根元(ローカル座標系の原点)の速度 ${\boldsymbol v}_j$ が以下の式で計算する。

{\boldsymbol w_j} =  {\boldsymbol w_{j-1}} + ({\bf R}_{j-1} \vec{{\boldsymbol a_j}})\dot{q}_j~,  \tag{3}

{\boldsymbol v_j} = {\boldsymbol v_{j-1}} + {\boldsymbol w_{j-1}} \times ({\bf R}_{j-1} \vec{{\boldsymbol b_j}}) \tag{4}

ここでの変数の定義は以下の通り:

• サフィックス $j-1$: リンク $j$ の親リンク
• ${\bf R}_{j}$: リンク $j$ の姿勢行列
• $\vec{{\boldsymbol a}_{j}}$: リンク $j$ の軸ベクトル(リンク $j$ の根元にあるローカル座標系からみたベクトル)
• $\vec{{\boldsymbol b}_{j}}$: リンク $j-1$ のローカル座標系からみたリンク $j$ の根元にあるローカル座標系の位置ベクトル
• $\dot{q}_j$: 関節jの回転速度

また、姿勢行列の微分は以下の式で計算するので、

\dot{{\bf R}}_j = {\boldsymbol w}_j \times {\bf R}_j \tag{5}

${\boldsymbol w}_j$ と ${\boldsymbol v}_j$ の微分はそれぞれ以下の式で計算する。

 \begin{aligned}
\dot{{\boldsymbol w}}_j = & ~ \dot{{\boldsymbol w}}_{j-1} + {\boldsymbol w}_{j-1} \times  {\bf R}_{j-1} \vec{{\boldsymbol a}_j} \dot{q}_j + ({\bf R}_{j-1} \vec{{\boldsymbol a}_j})\ddot{q}_j ~, \\
\dot{{\boldsymbol v}}_j = & ~ \dot{{\boldsymbol v}}_{j-1} + \dot{{\boldsymbol w}}_{j-1} \times ( {\bf R}_{j-1} \vec{{\boldsymbol b}_j} ) +  ({\boldsymbol w}_{j-1} \times ( {\boldsymbol w}_{j-1} \times {\bf R}_{j-1} \vec{{\boldsymbol b}_j}) )
 \end{aligned}
\tag{6}

ニュートンオイラー方程式

変数の定義は以下の通り:

• ${\boldsymbol f}$: 重心に作用する並行力
• $m$: 質量
• ${\boldsymbol c}$: 重心位置
• ${\boldsymbol \tau}_c$: 重心に作用するトルク
• ${\bf I}$: 慣性テンソル
• ${\bar{\bf I}}$: 基準姿勢における慣性テンソル

    \left\{
    \begin{aligned}
    {\boldsymbol f} = &  m \ddot{{\boldsymbol c}} \\
    {\boldsymbol {\tau}} _c = & \displaystyle {\frac{d}{dt}} {\bf I}{\boldsymbol w} =  {\bf I}\dot {\boldsymbol w} + {\boldsymbol w} \times {\bf I}{\boldsymbol w}
    \end{aligned}
    \right.
\tag{7}

ここで慣性テンソルは基準姿勢における慣性テンソルから以下の式で求める:

{\bf I} = {\bf R} {\bar{\bf I}} {\bf R}^{\rm T} \tag{8}

空間速度で表すニュートンオイラー方程式

重心位置の空間速度は以下の式で計算する。

{\boldsymbol v}_o = {\dot{\boldsymbol c}} - {\boldsymbol w} \times {\boldsymbol c} \tag{9}

式9を微分すると以下の式になる:

{\dot {\boldsymbol v}_o} = {\ddot{\boldsymbol c}} - {\dot{\boldsymbol w}} \times {\boldsymbol c} - {\boldsymbol w} \times {\dot {\boldsymbol c}} \tag{10}

式9の ${\dot{\boldsymbol c}}$ を式10 に代入すると式10 を以下の式で書き直す:

{\ddot{\boldsymbol c}} = {\dot {\boldsymbol v}_o} -  {\boldsymbol c} \times {\dot{\boldsymbol w}} + {\boldsymbol w} \times ({\boldsymbol v}_o + {\boldsymbol w} \times {\boldsymbol c} ) \tag{11}

これを式 7 に代入すると以下の式になる。

{\boldsymbol f} = m({\dot {\boldsymbol v}_o} - {\boldsymbol c} \times {\dot{\boldsymbol w}} + {\boldsymbol w} \times ({\boldsymbol v}_o + {\boldsymbol w} \times {\boldsymbol c} )) \tag{12}

式 12 を式 7 に代入すると以下の式が導出される:

 {\boldsymbol {\tau}} = {\boldsymbol {\tau}}_c + {\boldsymbol c} \times {\boldsymbol f} =  {\bf I}{\dot {\boldsymbol w}} + {\boldsymbol w} \times {\bf I}{\boldsymbol w} + m {\boldsymbol c} \times ({\dot {\boldsymbol v}_o} - {\bf c} \times {\dot{\boldsymbol w}} + {\boldsymbol w} \times ({\boldsymbol v}_o + {\boldsymbol w} \times {\boldsymbol c} )) \tag{13}

式12 と式 13を行列でまとめると以下の式になる。

\begin{bmatrix}
{\boldsymbol f} \\
{\boldsymbol {\tau}}
\end{bmatrix}  = {\bf I}^s \begin{bmatrix} \dot{\boldsymbol v}_o \\ \dot{\boldsymbol w} \end{bmatrix} + \begin{bmatrix} {\hat{\boldsymbol w}}  & {\boldsymbol 0} \\ {\hat{\boldsymbol v}_o} & {\hat{\boldsymbol w}}  \end{bmatrix}  {\bf I}^s \begin{bmatrix} {\boldsymbol v}_o \\ {\boldsymbol w} \end{bmatrix} \tag{14}

ここで、空間慣性行列 ${\bf I}^s$ と ^ (hat) の定義は以下の通り:

    \begin{aligned}
    {\bf I}^s \equiv & \begin{bmatrix} m{\bf E} & m{\hat{\boldsymbol c}^{\rm T}} \\ m{\hat{\boldsymbol c}} & m{\hat{\boldsymbol c}}{\hat{\boldsymbol c}^{\rm T}} + {\bf I}  \end{bmatrix} \\
    {\bf E} \equiv & \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1  \end{bmatrix} \\
    {\hat {\boldsymbol x}} \equiv & \begin{bmatrix} 0 & -x_z & x_y \\ x_z & 0 & -x_z \\ -x_y & x_x & 0  \end{bmatrix} \\
    \end{aligned} \tag{15}

関節トルクの計算

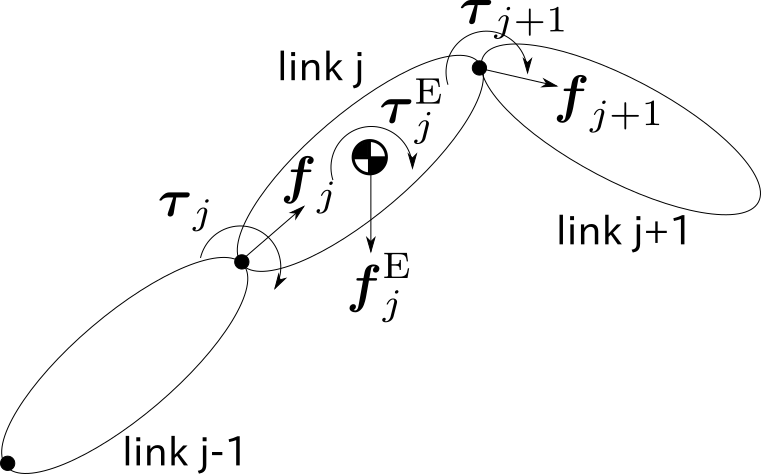
リンク $j$ の運動が以下の要素で引き起こしている。

• 外部から作用する力とベクトル $[{\boldsymbol f}_j^{\rm E} ~~{\boldsymbol \tau _j}^{\rm E}]^{\rm T}$
• 根元側から作用する力とベクトル $[{\boldsymbol f}_{j} ~~ {\boldsymbol {\tau _j}}]^{\rm T}$
• 子リンクからの反作用力とベクトル $-[{\boldsymbol f}_{j+1} ~~ {\boldsymbol \tau _{j+1}}]^{\rm T}$

運動方程式が以下になる:

\begin{bmatrix} {\boldsymbol f}_j \\ {\boldsymbol \tau}_j  \end{bmatrix} + \begin{bmatrix} {\boldsymbol f}_j^{\rm E} \\ {\boldsymbol \tau}_j^{\rm E}  \end{bmatrix} - \begin{bmatrix} {\boldsymbol f}_{j+1} \\ {\boldsymbol \tau}_{j+1}  \end{bmatrix} =
{\bf I}_j^s \begin{bmatrix} \dot{\boldsymbol v}_{oj} \\ \dot{\boldsymbol w}_j \end{bmatrix} + \begin{bmatrix} {\hat{\boldsymbol w}_j}  & {\boldsymbol 0} \\ {\hat{\boldsymbol v}_{oj}} & {\hat{\boldsymbol w}_j}  \end{bmatrix}  {\bf I}_j^s \begin{bmatrix} {\boldsymbol v}_{oj} \\ {\boldsymbol w}_j \end{bmatrix} \tag{16}

ここで ${\bf I}_j^s$ がリンク $j$ の空間慣性行列で以下の通りで定義する：

{\bf I}_j^s \equiv \begin{bmatrix} m{\bf E} & m{\hat{\boldsymbol c}_j^{\rm T}} \\ m{\hat{\boldsymbol c}_j} & m{\hat{\boldsymbol c}_j} {\hat{\boldsymbol c}_j^{\rm T}} + {\bf I}_j  \end{bmatrix} \tag{17}

根元側から作用する力とベクトル以外を右辺に持っていくと以下の式になる。

\begin{bmatrix} {\boldsymbol f}_j \\ {\boldsymbol \tau}_j  \end{bmatrix} =
{\bf I}_j^s \begin{bmatrix} \dot{\boldsymbol v}_{oj} \\ \dot{\boldsymbol w}_j \end{bmatrix} + \begin{bmatrix} {\hat{\boldsymbol w}_j}  & {\boldsymbol 0} \\ {\hat{\boldsymbol v}_{oj}} & {\hat{\boldsymbol w}_j}  \end{bmatrix}  {\bf I}_j^s \begin{bmatrix} {\boldsymbol v}_{oj} \\ {\boldsymbol w}_j \end{bmatrix}
 - \begin{bmatrix} {\boldsymbol f}_j^{\rm E} \\ {\boldsymbol \tau}_j^{\rm E}  \end{bmatrix} + \begin{bmatrix} {\boldsymbol f}_{j+1} \\ {\boldsymbol \tau}_{j+1}  \end{bmatrix} \tag{18}

式2から、 $\dot{\boldsymbol v}_{oj}$ が以下の式で計算する:

\dot{{\boldsymbol v}}_{oj} = \dot{{\boldsymbol v}_j} - \dot{{\boldsymbol w}_j} \times {\boldsymbol p}_j - {\boldsymbol w}_j \times {\boldsymbol v}_j \tag{19}

関節軸jに発生するトルクは以下の式で計算できる。

u_j = \begin{bmatrix} {\boldsymbol p}_j  \times {\bf R}_{j} \vec{{\boldsymbol a}_{j}} \\  {\bf R}_{j} \vec{{\boldsymbol a}_{j}}  \end{bmatrix}^{\rm T} \begin{bmatrix} {\boldsymbol f}_j \\ {\boldsymbol \tau}_j \end{bmatrix} + I_j^{\rm rotor}\ddot{q}_j \tag{20}

ここで、$I_j^{\rm rotor}$ は関節軸jのローターイナーシャである。

まとめ

各軸のトルクは以下の手順で計算できる

1. 全軸の角度、角速度、角加速度を設定
2. 根元の軸から末端の軸へ順に加速度まで考慮する順運動学計算
3. 各リンクに外力加える(重力)$[{\boldsymbol f}_j^{\rm E} ~~{\boldsymbol \tau _j}^{\rm E}]^{\rm T}$
4. 末端の軸から根本の軸へ順にトルクを計算する

choreonoidのライブラリを用いた実装サンプル

cnoid::Vector3 g = cnoid::Vector3(0, 0, -9.80665); // 重力ベクトル
if (!q_deque.empty()) {　// 時系列の関節軌道をq_dequeを予め入れとく
  for (int i=0; i<m_dof; i++) {
  m_robot -> joint(i) -> q() = q_deque.at(0)[i]; //m_robotがBodyPtr
  m_robot -> joint(i) -> dq() = (q_deque.at(0)[i] - q_pre[i]) / m_dt;　// m_dtが制御周期
  m_robot -> joint(i) -> ddq() = (m_robot -> joint(i) -> dq() - v_pre[i]) /  m_dt;       
  q_pre[i] = q_deque.at(0)[i];
  v_pre[i] = m_robot -> joint(i) -> dq();
  }
  q_deque.pop_front();
  m_robot->calcForwardKinematics(true, true);　 // 加速度まで考慮する順運動学計算
  // 重力をかける。一旦zeroにresetする。じゃないと加算される
  for (int i=0; i<m_dof; i++) {
      m_robot -> joint(i) -> tau_ext() = cnoid::Vector3d::Zero();
      m_robot -> joint(i) -> f_ext() = cnoid::Vector3d::Zero();
      m_robot -> joint(i) -> addExternalForce(g * m_robot->joint(i)->m(), m_robot->joint(i)->c());
    }
    calcInverseDynamics(m_robot->rootLink()); // 全軸逆運動学計算
　　// 以下全軸のトルクにアクセスする
    for (int i=0; i<m_dof; i++) {
      cout << m_robot -> joint(i) -> u() << " ";
    }
    cout << endl;
 }

注意喚起

いままでバグったchoreonoid逆動力学計算関数がこのコミットおいて初めて修正された：

• cbcedc8 Fix the inverse dynamics calculation

これがchoreonoid v.1.7.0以後の修正なので、この関数を使いたい方はこのコミットあとのバージョンにしてください。
またchoreonoidの逆運動学計算関数はロータインナーシャルまで考慮されている。他の計算ライブラリや自分の手計算と比較するときにはロータインナーシャルの項も意識しよう。

次回を待て！！