はじめに
メリークリスマス!
フューチャーAdventCalender2 2021の25日目(The last of this year!)です。
今年で入社6年目になりますが、趣味は相変わらずパズルとそれらを解くためのアルゴリズムです。
一昨年のクリスマスのアドベントカレンダーでNxNxNのルービックキューブの通用的な解法の記事を書きましたが、今回はNxNxNのルービックキューブに限らず、汎化したツイスティパズル(twisty puzzle)のソルバーを実装しました。
ツイスティパズルとは
ざっとルービックキューブの汎化と理解しても問題はありません。
ルービックキューブのように、複数のピースで構成された層が、互いに独立した各軸に沿って回転できるパズルであり、
一連の操作によってさまざまな組み合わせに操作できるパズルです。このようなパズルの形状は、多くは多面体ですが、それに限らず、物理上作れなくても数学的に定義したモデルも含まれます。
Wikipedia上、別名称(Combination puzzle 組み合わせパズル)での紹介ページはあります。
NxNxNのルービックキューブはもちろん、いろんな変種「キューブ」や知育玩具(の一部)もこの種の属しています。
例えば、
- スキューブ
- ピラミンクス
- メガミンクス
- テンビリオン(昔の任天堂はこんなパズルも作ってましたね、意外)
- Topspin(立体に限らず、平面のものもあります)
- and so many (パズル紹介のJaap's Puzzle Pageが有名)
特に面白いのは、4Dや5Dなどの多次元のキューブです。実物は実現できないですが、シミュレーターで楽しむことはできます。

これは筆者のパズルのコレクションの一部です。(関係ないものも入ってしまい、ご勘弁を)
解けないやつもありますので、それらを見たらいらいらします。😾
ソルバーとは
ここのソルバーは、上記のツイスティパズルに対して、任意のランダム状態から初期状態に戻す操作手順を求めるアルゴリズムの実装プログラムのことです。
もちろん、ツイスティパズルに、簡単なやつもあればとんでもなく複雑なものや爆発的な組み合わせ状態数のやつも当然あります。天文学的数字の状態から正しい遷移のルートを導き出すのは、人間で解くのももちろん無理ですし、一定の量に超えたら、スーパーコンピュータでも、量子コンピューターでも無能の羽目になります。なので、論理上は無限な時間やメモリーを与えられたら必ず。現実を考えるとやはりリソースの制限内でやれることを最適化する必要があります。(結果を待つ人間の寿命が有限ですし、宇宙で利用できるエネルギーも有限のはず)
既存のソルバーは色々ありますが、(例えばこのオンラインツール)それらは、ほとんど3X3X3のルービックキューブ、もしくは特定の一種のパズルに限定されています。
今回のソルバー実装の着眼点は「汎化」です。
自分は実装したツイスティパズルのソルバーは以下の特徴を持つツイスティパズルに限定しますが、わりと表現力が強く、既存の数百種のパズルを表現でき、更にカスタマイズ定義したパズルも新に作り出すことも可能です。
- 操作の前後は、ピースの数や種類が変わらない
- 操作の前後は、パズル全体の形が変わらない
- どんな状態に遷移したとしても、許す操作はすべて適用できる(下図のようなブロックパーツがあるやつには対応しない)

パズルをどう定義するか
状態の表現
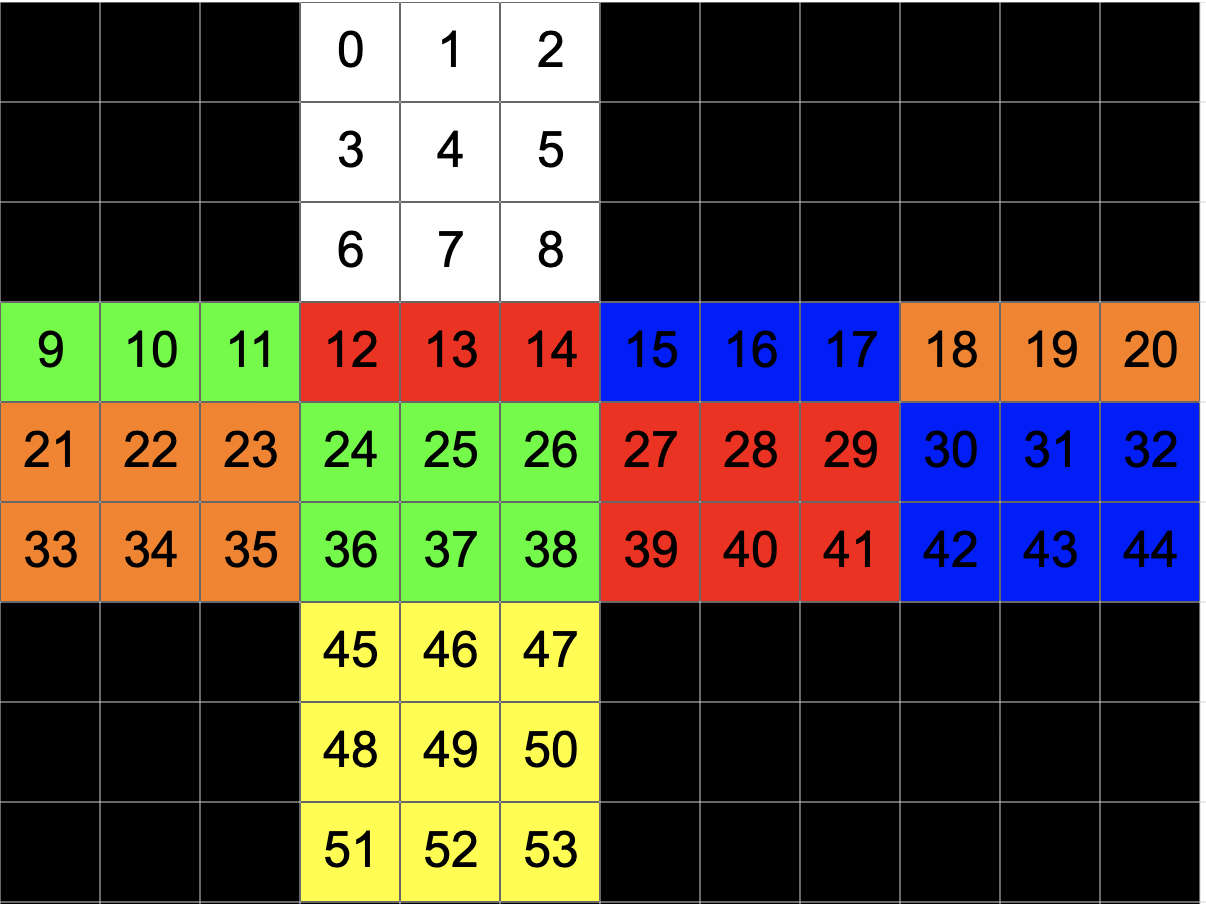
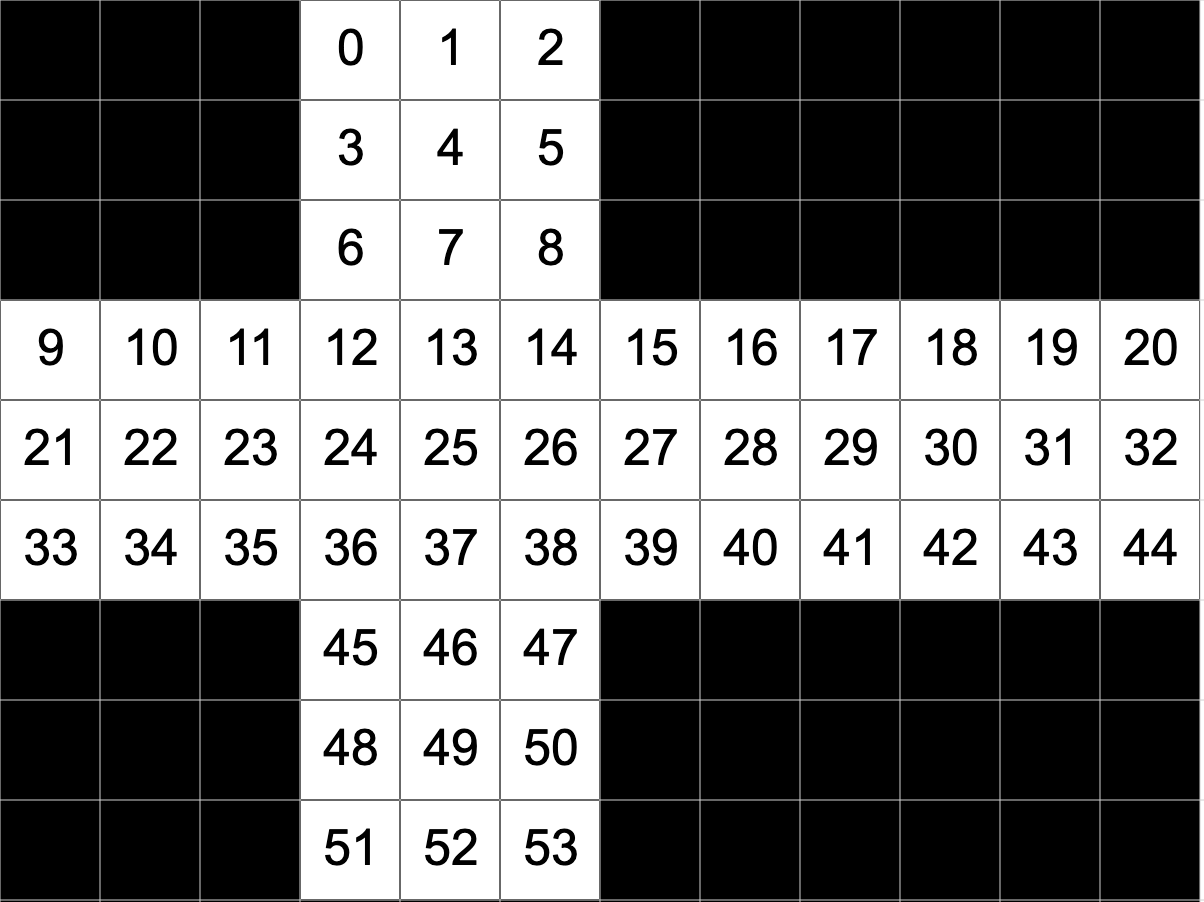
まずは、パズルに構成する最小単位としての「ピース」に番号をふっていきます。下図は普通の3X3X3のルービックキューブの平面展開図に番号を付与するイメージです。(多数のプログラミング言語の習慣に沿って"0-index"にしています。)
初期状態の定義
各ピースの初期状態(完成状態)は固有のカラーが持っています。それもパズルの定義の一部になります。

プログラムを扱いやすいため、各カラーに1文字のアルファベットを名付けて、付与した番号順に1個の文字列で現在の状態が
W:white, O:orange, G:green, R: red, B: blue, Y: yellow
初期状態を表す文字列は"WWWWWWWWWOOOGGGRRRBBBOOOGGGRRRBBBOOOGGGRRRBBBYYYYYYYYY"になります。
操作の定義
次は肝心なパズルの「操作」の定義です。
まずは操作名について、特別なルールは問わなくても良いですが、ここで説明しやすいために、一般的なルービックキューブ操作の表記法を採用して説明します。
各層に名付けて(上U、下D、左L、右R、前F、後B)層の回転は時計回りは名称そのまま、反時計回りなら名称の後に'を付け、180度回転なら名称の後に2を付けるのが一般的な表記法です。
例えば、上記の採番を使ったら、回転U(上の層を時計回り90度回す)の定義は下になります。
# 上の面の角の移動
0番目のピースを2番に移動
2番目のピースを8番に移動
8番目のピースを6番に移動
6番目のピースを0番に移動
# 上の面の辺の移動
1番目のピースを5番に移動
5番目のピースを7番に移動
7番目のピースを3番に移動
3番目のピースを1番に移動
# 層は一全体なので、上の面だけではなく、周りのピースも連動
9番目のピースを18番に移動
18番目のピースを15番に移動
15番目のピースを12番に移動
12番目のピースを9番に移動
10番目のピースを19番に移動
19番目のピースを16番に移動
16番目のピースを13番に移動
13番目のピースを10番に移動
11番目のピースを20番に移動
20番目のピースを17番に移動
17番目のピースを14番に移動
14番目のピースを11番に移動
このように、数や種類が変わらなく、場所だけ入れ替わる操作は、数学的に「群」で定義されています。
([余談]群論のWikipediaページにルービックキューブの画像もある)
上例の入れ替わる操作の数学的な表記は(0 2 8 6)(1 5 7 3)(9 18 15 12)(10 19 16 13)(11 20 17 14)で表現できます。各カッコに入れ替えの小さいループの箇所番号で表現しています。
ちなみに、ループなので、(0 2 8 6)と(2 8 6 0)と(8 6 2 0)などは同じ意味しています。揺らぎをなくすために一般的に一番小さい数値が先頭に来るような表現を採用します。
カッコ内の数値の順番が意味ありますが、カッコの塊同士間の順番は意味ありません。(0 2 8 6)(1 5 7 3)と(1 5 7 3)(0 2 8 6)は一緒です。同じく、揺らぎをなくすために、頭数値の小さい順で並べば良いでしょう。
プログラミングしやすいように下のように一次元の配列で表現できるように工夫しました。
小さいループの区切り部分は頭の数値をもう一度要素の出現することで表現しています。(スペースを開けたのは見やすいため)
"U" : [0,2,8,6,0, 1,5,7,3,1, 9,18,15,12,9, 10,19,16,13,10, 11,20,17,14,11]
それの逆操作U'は、基本全部逆したら良いですが、前述のように揺らぎを気になって、小さい数値を先頭に来るように下記になります。
"U'" : [0,6,8,2,0, 1,3,7,5,1, 9,12,15,18,9, 10,13,16,19,10, 11,14,17,20,11]
もう1個の例を挙げると、上層を180度回転する操作はこうなります。
"U2" : [0,8,0, 1,7,1, 2,6,2, 3,5,3,
9,15,9, 10,16,10, 11,17,11, 12,18,12, 13,19,13, 14,20,14]
二次元配列よりは少し冗長になりますが、データ構造はちょっとシンプルです。このような一次元配列を使ったロジックの実装も簡潔になるのもメリットです(頻繁に行う処理なので、余計なデータ操作を減らすと性能向上にも繋がる)。
下記擬似コードのロジックで、操作が定義の順にtemp変数と入れ替わることだけで、「旧状態 --操作--> 新状態」の状態遷移ロジックはシンプルに実現できます。
// operationListは上記述べた操作を定義している一次元の配列
// 例:[0,2,8,6,0, 1,5,7,3,1, 9,18,15,12,9, 10,19,16,13,10, 11,20,17,14,11]
// stateは状態を表す文字列
// 例:"WWWWWWWWWOOOGGGRRRBBBOOOGGGRRRBBBOOOGGGRRRBBBYYYYYYYYY"
temp = '' // 交換用臨時変数、初期値は何でも良い
for (i = 0; i < operationList.length; ++i) {
v = operationList[i]
swap(state[v], temp)
}
// 操作後の結果
// state: "WWWWWWWWWGGGRRRBBBOOOOOOGGGRRRBBBOOOGGGRRRBBBYYYYYYYYY"
// tempは初期値に戻る
他の各操作D,L,R,F,B、そしてそれらのX',X2を定義していくだけで、省略します。
以上は、汎用的なツイスティパズルの状態表現(採番)、初期状態、操作の定義、及びプログラミングでの表現方法です。
パズルをどう解くか
ルービックキューブは、1層ずつ完成させるような初心者向けの手順とかありますね。それに沿って実装するのは良いですが、それの欠点も明らかです。①ケアするケースはかなりあり実装上困難、②冗長なステップが多数あり最適解ではありません。そもそも、任意に定義されたパズルの汎用的なソルバーは固定の手順はございませんね。
最短手順もしくはなるべく短い手順を探すには探索のアルゴリズムを使うのです。
一概に探索といっても、いろんなテクニックがあります。一段ずつレベルアップして実装してみました。
(以下のソースは、読みやすいために、Python3バージョンの実装を貼っています。性能的に優れていなく、数秒で2X2X2のキューブを解けたり解けなかったりします。もっと性能を出せるために実際のプログラムはGolangで書き換えていますが、ソースの構造が複雑になり、説明に適切ではないので割愛。どの実装でもロジックは一緒です。)
【梅レベル】単純な幅優先探索
プロトタイプとして、実装量が一番少ないです。実行時間を気にしない、もしくは、状態数が少ない簡単なパズルの場合は、これを使ってもいいです。
- 解きたい状態(state)からスタートし、それをキュー(open_queue)の末尾入れます
- open_queueの先頭から1個のstateを取り出して、それの1ステップ後到達可能なすべてのnext_stateをopen_queueの末尾に追加します。ただし、next_stateは探索済みだったらスキップ、next_stateはゴールになったら終了
- 2.を繰り返します。
(close_dictは探索済みのstateをマークするためにもうけています)
class BFSSolver(PuzzleSolver):
def solve(self, state: PuzzleState) -> List[PuzzleTurn]:
if state.is_solved():
return []
open_queue = deque([state])
close_dict = {str(state): []}
while open_queue:
state = open_queue.pop()
turns = close_dict[str(state)]
for next_turn in state.gen_allowed_turns_for_solver():
next_state = state.get_next_state(next_turn)
next_state_key = str(next_state)
if next_state_key in close_dict:
continue
if next_state.is_solved():
return turns + [next_turn]
close_dict[next_state_key] = turns + [next_turn]
open_queue.appendleft(next_state)
【竹レベル】ヒューリスティックを導入した探索
2X2X2のキューブでも三百万以上の状態数を持っているらしいです。それより状態数が多いパズルには愚直のBFSを使うとやはりメモリーがパンクしてしまいます。
探索性能改善によく使われる手法はヒューリスティックの導入が挙げられます(A*アルゴリズムと呼ぶ)。今の状態からゴールに到達まで「最短でも何ステップは必要?」を高速で評価する関数はヒューリスティック関数と呼ばれます。例えば、障害物を持った地図上で起点と終点のパスを探す時、障害物を無視して、直線距離(もしくは格子上のマンハッタン距離)はヒューリスティック関数として使えます。
その評価関数h(x)があれば、探索のqueueから取り出す時、一番希望があるものを最優先的に見るので、結果にたどり着くのが早くなるはずです。もちろん、その加速の効果は、h(x)の精度によって変わります。
実現は単純な幅優先探索と似ていますが、単純のFIFOキューブの代わりに、優先度付きキューもしくはヒープを採用します。
優先度 = 過去探索したパスの距離(探索の途中で既知) + 将来かかりそうな距離h(x)
(数値が少ないほど優先)
- 解きたい状態(state)からスタートし、それを優先度付きキュー、ここではヒープ(open_heap)に入れます。優先度は
0 + h(state) - open_heapのから優先度数値が最も小さい1個のstateを取り出して、それの1ステップ後到達可能なすべてのnext_stateの優先度を計算し、open_heapに追加します。ただし、next_stateは探索済みだったらスキップ、next_stateはゴールになったら終了
- 2.を繰り返します。
更に
一般的には、ヒューリスティック関数h(x)は具体的な実際問題の特性によって選定するものであり、汎用的に事前定義をしづらいものです。
ツイスティパズルの特性は、元の問題の部分集合とするパーシャル問題が定義できます。例えば、ルービックキューブだったら一部のピースを無視する(色を黒く塗りつぶすイメージ)ことによってパーシャル問題を定義します。このパーシャル問題は、状態数がだいぶ減ったため、それを解くには何ステップが必要なのかは比較的に高速で計算できます。パーシャル問題が
ある状態stateを一部のピースをマスクしてmasked_stateとして、そのmasked_stateからゴール必要なステップ数step_to_goal(masked_state)は、元問題に対して「最短でも必要なステップ数」ですね。なので、それを適切なヒューリスティック関数として使えます。
実際によくあるやり方は、パーシャル問題のすべての状態のstep_to_goalの結果を事前処理として予めメモリ、あるいはファイルに保存しておいて、探索時h(x)を呼ぶ時は辞書から引きます。この手法は「パターンデータベース(PatternDatabase or PDB)」と呼ばれます。
ここのデモのソースに使ったヒューリスティックは、ルービックキューブの対面になる緑(G)と青(B)面だけ保留して、生成したPDBはこんな形です。(8.61 MB デモ用のため最適化していない)
## opposite_faces.txt
■■Y■■X■■Y■■X■■Y■■X■■Y■■X 0
■Y■■Y■■X■■X■■Y■■Y■■X■■X■ 0
■■X■■Y■■X■■Y■■X■■Y■■X■■Y 0
■X■■X■■Y■■Y■■X■■X■■Y■■Y■ 0
X■■X■■X■■X■■Y■■Y■■Y■■Y■■ 0
Y■■Y■■Y■■Y■■X■■X■■X■■X■■ 0
■■Y■■X■■Y■■X■X■■X■■Y■■Y■ 1
■Y■■Y■■X■■X■■■Y■■X■■Y■■X 1
■■X■■Y■■X■■Y■Y■■Y■■X■■X■ 1
■X■■X■■Y■■Y■■■X■■Y■■X■■Y 1
X■■■X■X■■■Y■Y■■■X■Y■■■Y■ 1
X■■X■■■■Y■■XY■■Y■■■■Y■■X 1
■Y■X■■■X■X■■■Y■Y■■■X■Y■■ 1
■■X■■YX■■X■■■■X■■YY■■Y■■ 1
■X■Y■■■Y■Y■■■X■X■■■Y■X■■ 1
...
■■Y■X■■Y■■X■Y■■■X■■■Y■X■ 8
■■Y■Y■■■X■■X■Y■Y■■■■X■■X 8
■X■■Y■■X■■■Y■X■■■Y■X■Y■■ 8
■■X■■X■Y■■■Y■■X■■XY■■■Y■ 8
■X■■X■■X■■X■Y■■■■Y■Y■Y■■ 8
■■X■■X■■X■■X■■YY■■Y■■■Y■ 8
■X■■X■■X■■X■Y■■■Y■■■YY■■ 8
■■X■■X■■X■■X■Y■Y■■Y■■■■Y 8
■X■Y■■■X■■■Y■X■■■Y■X■■Y■ 8
■■X■■X■Y■Y■■■■X■■X■■Y■Y■ 8
■■Y■X■Y■■■X■■Y■■X■■■Y■X■ 8
Y■■■Y■■■X■■X■Y■■■Y■■X■■X 8
■■YY■■Y■■■Y■■X■■X■■X■■X■ 8
Y■■■Y■■■YY■■■■X■■X■■X■■X 8
■Y■Y■■Y■■■■Y■X■■X■■X■■X■ 8
Y■■■■Y■Y■Y■■■■X■■X■■X■■X 8
■Y■X■■■■YX■■■■YX■■Y■■X■■ 8
■Y■■■YX■■X■■Y■■■Y■X■■X■■ 8
X■■■■YX■■■Y■X■■Y■■X■■■■Y 8
X■■X■■■■Y■Y■X■■X■■■Y■Y■■ 8
Y■■X■■■■YX■■■■YX■■■Y■X■■ 8
■Y■Y■■X■■X■■■■Y■Y■X■■X■■ 8
X■■■■YX■■Y■■X■■■Y■X■■■■Y 8
X■■X■■Y■■■Y■X■■X■■■Y■■■Y 8
下のソースコードにPDBファイルの生成、読み込み、パーシャル問題に変換用のマスク処理(__state_to_pattern)などのロジックは全部入っています。
class PdbAStarSolver(PuzzleSolver):
# pattern variables
X = "X"
Y = "Y"
PDB_PATH = "twisty_puzzle/solver/pattern_db/opposite_faces.txt"
@classmethod
def __state_to_pattern(
cls, state: PuzzleState, pattern_map: Dict[str, str]) -> PuzzleState:
new_state_value = np.full_like(
state.state_value, RubikCubeColor.UNDEFINED.value)
for map_from, map_to in pattern_map.items():
new_state_value = np.where(
state.state_value == map_from, map_to, new_state_value)
return state.__class__(state.size, new_state_value)
def build_pdb(self) -> Dict[str, int]:
print("Building pattern database ...")
init_pattern = self.__state_to_pattern(
self.state_cls.get_init_state(self.size),
{RubikCubeColor.GREEN.value: "X", RubikCubeColor.BLUE.value: "Y"})
print(init_template(self.size).format(init_pattern.state_value))
open_queue = deque([init_pattern])
close_dict = {
str(sym_pattern): 0
for sym_pattern in init_pattern.get_symmetric_states()
}
while open_queue:
last_pattern = open_queue.pop()
last_steps = close_dict[str(last_pattern)]
for next_turn in last_pattern.gen_allowed_turns_for_solver():
next_pattern = last_pattern.get_next_state(next_turn)
if str(next_pattern) in close_dict:
continue
for sym_pattern in next_pattern.get_symmetric_states():
sym_state_key = str(sym_pattern)
close_dict[sym_state_key] = close_dict.get(
sym_state_key, last_steps + 1)
open_queue.appendleft(next_pattern)
print("Pattern database built.")
return close_dict
def evaluate_step_num(self, state: PuzzleState) -> int:
max_steps = 0
for axis_1, axis_2 in ((Axis.X, Axis.negX),
(Axis.Y, Axis.negY),
(Axis.Z, Axis.negZ)):
color_x = axis_1.color().value
color_y = axis_2.color().value
pattern = self.__state_to_pattern(
state, {color_x: self.X, color_y: self.Y})
max_steps = max(max_steps, self.pdb[str(pattern)])
return max_steps
def solve(self, state: PuzzleState) -> List[PuzzleTurn]:
if state.is_solved():
return []
cnt = count() # a heap comparator helper
open_heap = [(self.evaluate_step_num(state), next(cnt), state)]
close_dict = {str(state): []}
while open_heap:
_, _, last_state = heappop(open_heap)
turns = close_dict[str(last_state)]
for next_turn in last_state.gen_allowed_turns_for_solver():
next_state = last_state.get_next_state(next_turn)
next_state_key = str(next_state)
if next_state_key in close_dict:
continue
if next_state.is_solved():
return turns + [next_turn]
close_dict[next_state_key] = turns + [next_turn]
heappush(open_heap, (
len(turns) + 1 + self.evaluate_step_num(next_state),
next(cnt),
next_state))
def __load_pdb(self, force_update_pdb: bool) -> Dict[str, int]:
if force_update_pdb or not path.exists(self.PDB_PATH):
# create pdb
pdb = self.build_pdb()
# write pdb into file
with open(self.PDB_PATH, mode="w") as file:
for key, value in pdb.items():
file.write(key)
file.write(" ")
file.write(str(value))
file.write("\n")
else:
# load pdb from file
pdb = {}
with open(self.PDB_PATH) as file:
for line in file.readlines():
key, value = line.split()
pdb[key] = int(value)
return pdb
def __init__(self,
size: int = 2,
force_update_pdb: bool = False):
self.state_cls = RubikCubeState
self.size = size
self.pdb = self.__load_pdb(force_update_pdb)
【松レベル】双方向探索とヒューリスティックと組み合わせ
鉛筆で迷路を解いたことあるでしょうか。スタートからやる派とゴールからやる派がいると思いますが、スタートでやってみて、行き詰まったらゴールからもやって、またスタートからやり途中の探索を続けて、交互にやり続けて、真ん中ぐらいに合流すれば解決になるスタイルは双方向探索です。
こういうやり方は実装が複雑になり、他に特にメリットがないと感じられる方がいらっしゃるかもしれません。計算量視点から考えてみましょう。
また3X3X3のルービックキューブを例とします。ルービックキューブを任意にスクランブルして、どんな難しいケースでも20ステップ以内で解けることが証明されました。そして、ルービックキューブに絶対に20より少ないステップ数で解けない状態が存在することも証明されました。20の数字はルービックキューブのGod's Numberと言います。
ルービックキューブの操作U D L R F BそしてそれらのX' X2バージョンを含め、全部の操作は18個とすると、20ステップ後は概ねの探索量は18^20 ≈ 10^25状態がある(重複のケースを一旦無視)、一方、両端からそれぞれ10ステップを探索して、中間でどこか合流したら、探索量は2 * 18^10 ≈ 10^13状態だけがあり、結果1兆倍少ないですね!
具体的な実装は頭から順とゴールからの探索を1ステップずつ交互にして、どちらも現在探索の先端が相手の探索済みの集合に存在するかどうかを常にチェックして、存在すれば交流点が見つかります。最短解を求めるのは更に探索続けてる必要がりますが、次善のソリューションでも許して、アルゴリズムをとにかく早く終了したい場合は、これで終了し、スタートからゴールに繋ぐ最終的なパス合成して終わりです。
下は双方向BFSの実装例です。
class BidirectionalBFSSolver(PuzzleSolver):
@staticmethod
def __bfs_search_one_step(
open_queue: Deque[PuzzleState],
this_close_dict: Dict[str, PuzzleTurn],
that_close_dict: Dict[str, PuzzleTurn]) -> Optional[PuzzleState]:
last_state = open_queue.pop()
for next_turn in last_state.gen_allowed_turns_for_solver():
next_state = last_state.get_next_state(next_turn)
next_state_key = str(next_state)
if next_state_key in this_close_dict:
continue
open_queue.appendleft(next_state)
this_close_dict[next_state_key] = next_turn
if next_state_key in that_close_dict:
return next_state
return None
@staticmethod
def __recover_turns(forward_dict: Dict[str, PuzzleTurn],
backward_dict: Dict[str, PuzzleTurn],
meet_state: PuzzleState) -> List[PuzzleTurn]:
forward_turns = []
backward_turns = []
state = meet_state
while True:
turn = forward_dict[str(state)]
if turn is None:
break
forward_turns.append(turn)
state = state.get_next_state(turn.get_reverse())
state = meet_state
while True:
turn = backward_dict[str(state)]
if turn is None:
break
turn = turn.get_reverse()
backward_turns.append(turn)
state = state.get_next_state(turn)
return list(reversed(forward_turns)) + backward_turns
def solve(self, state: PuzzleState) -> List[PuzzleTurn]:
if state.is_solved():
return []
goal_state = state.get_init_state(state.size)
backward_queue = deque(goal_state.get_symmetric_states())
backward_dict = {
str(final_state): None for final_state in backward_queue}
state_key = str(state)
if state_key in backward_dict:
return []
forward_queue = deque([state])
forward_dict = {state_key: None}
while forward_queue and backward_queue:
# forward
meet_state = self.__bfs_search_one_step(
forward_queue, forward_dict, backward_dict)
if meet_state is not None:
break
# backward
meet_state = self.__bfs_search_one_step(
backward_queue, backward_dict, forward_dict)
if meet_state is not None:
break
return self.__recover_turns(forward_dict, backward_dict, meet_state)
ヒューリスティックと組み合わせ、更に加速化はできます。
すべてを繋げて
上は実装したパーツとパーツの紹介になりました。もっとイメージを湧くように、実際に1個新しいパズルの定義からソルバーを動かすまで紹介します。
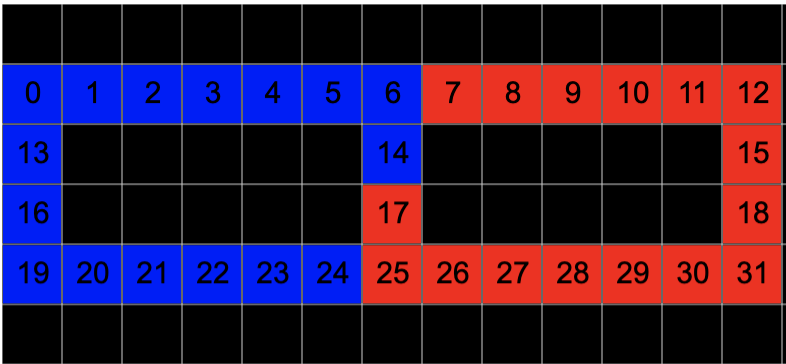
ボールリングというパズルを対象にします。真ん中の4つのボールが入ったスロットは、左あるいは右にスライドできます。左に寄せた時は左のリング全体が回せますし、右に寄せた時は右のリング全体が回せます。

実際に定義をyaml形式に落とし込むとこのようになります。
Lはスロットが左に寄せた状態で、左のリングを1ステップを時計回りに回すのを表し、
Rはスロットが右に寄せた状態で、右のリングを1ステップを時計回りに回すのを表し、
extenderは操作の定義の手間を少し減らせるためです。LとRそれぞれので反時計回り回す操作のL'とR'で簡略的に定義しています。
# ⓪①②③④⑤⑥⑦⑧⑨⑩⑪⑫
# ⑬ ⑭ ⑮
# ⑯ ⑰ ⑱
# ⑲⑳㉑㉒㉓㉔㉕㉖㉗㉘㉙㉚㉛
# 🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
# 🔵 🔵 🔴
# 🔵 🔴 🔴
# 🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
# BBBBBBBRRRRRR
# B B R
# B R R
# BBBBBBRRRRRRR
name: ball_ring
turnSet:
baseTurns:
- name: L
value: [0, 1, 2, 3, 4, 5, 6, 14, 17, 25, 24, 23, 22, 21, 20, 19, 16, 13, 0]
- name: R
value: [6, 7, 8, 9, 10, 11, 12, 15, 18, 31, 30, 29, 28, 27, 26, 25, 17, 14, 6]
extenders:
- name: L'
function: REVERSE
params:
- L
- name: R'
function: REVERSE
params:
- R
colorSetName: ball_ring
representationName: ball_ring
goal:
finalState: [B, B, B, B, B, B, B, R, R, R, R, R, R, B, B, R, B, R, R, B, B, B, B, B, B, R, R, R, R, R, R, R]
それのランダムの状態からソルバーを動かして、こんな結果になります。
==========================
puzzle meta: ball_ring
scramble: 1000 times
==========================
puzzle instance:
🔵🔴🔴🔵🔵🔴🔴🔵🔴🔴🔴🔵🔴
🔴 🔴 🔴
🔵 🔵 🔴
🔵🔵🔵🔴🔵🔵🔵🔵🔴🔴🔴🔵🔵
solving by Bidirectional-A* ...
solved by 26 steps
forward open: 8920, close: 14421
backward open: 7178, close: 12680
calculated in 0.04s
solved in 0.04s
answer: [L R L L R' R' L L R' L R' R' R' L R' R' L R' R' R' L R' L L L R]
length: 26
result verified: true
L:
🔴🔵🔴🔴🔵🔵🔴🔵🔴🔴🔴🔵🔴
🔵 🔴 🔴
🔵 🔴 🔴
🔵🔵🔴🔵🔵🔵🔵🔵🔴🔴🔴🔵🔵
R:
🔴🔵🔴🔴🔵🔵🔴🔴🔵🔴🔴🔴🔵
🔵 🔴 🔴
🔵 🔵 🔴
🔵🔵🔴🔵🔵🔵🔵🔴🔴🔴🔵🔵🔴
L:
🔵🔴🔵🔴🔴🔵🔵🔴🔵🔴🔴🔴🔵
🔵 🔴 🔴
🔵 🔴 🔴
🔵🔴🔵🔵🔵🔵🔵🔴🔴🔴🔵🔵🔴
L:
🔵🔵🔴🔵🔴🔴🔵🔴🔵🔴🔴🔴🔵
🔵 🔵 🔴
🔵 🔴 🔴
🔴🔵🔵🔵🔵🔵🔴🔴🔴🔴🔵🔵🔴
R':
🔵🔵🔴🔵🔴🔴🔴🔵🔴🔴🔴🔵🔴
🔵 🔵 🔴
🔵 🔵 🔴
🔴🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔵🔵
R':
🔵🔵🔴🔵🔴🔴🔵🔴🔴🔴🔵🔴🔴
🔵 🔴 🔴
🔵 🔵 🔵
🔴🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔵
L:
🔵🔵🔵🔴🔵🔴🔴🔴🔴🔴🔵🔴🔴
🔵 🔵 🔴
🔴 🔴 🔵
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔵
L:
🔵🔵🔵🔵🔴🔵🔴🔴🔴🔴🔵🔴🔴
🔴 🔴 🔴
🔵 🔵 🔵
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔵
R':
🔵🔵🔵🔵🔴🔵🔴🔴🔴🔵🔴🔴🔴
🔴 🔴 🔵
🔵 🔴 🔵
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔴🔵🔵🔵🔵🔴🔵🔴🔴🔵🔴🔴🔴
🔵 🔴 🔵
🔵 🔴 🔵
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔴🔵🔵🔵🔵🔴🔴🔴🔵🔴🔴🔴🔵
🔵 🔵 🔵
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔴🔵🔵🔵🔵🔴🔴🔵🔴🔴🔴🔵🔵
🔵 🔴 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔴🔵🔵🔵🔵🔴🔵🔴🔴🔴🔵🔵🔴
🔵 🔴 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔴🔵🔵🔵🔵🔴🔴🔴🔴🔵🔵🔴
🔵 🔵 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔴🔵🔵🔵🔵🔴🔴🔴🔵🔵🔴🔴
🔵 🔴 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔴🔵🔵🔵🔵🔴🔴🔵🔵🔴🔴🔴
🔵 🔴 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔵🔴🔵🔵🔵🔵🔴🔵🔵🔴🔴🔴
🔵 🔴 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔵🔴🔵🔵🔵🔴🔵🔵🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔵🔴🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴
🔵 🔴 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔵🔴🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔵🔵🔴🔵🔵🔵🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R':
🔵🔵🔵🔴🔵🔵🔴🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔵🔵🔵🔴🔵🔵🔴🔴🔴🔴🔴🔴
🔵 🔴 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔵🔵🔵🔵🔴🔵🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
L:
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔵 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
R:
🔵🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴
🔵 🔵 🔴
🔵 🔴 🔴
🔵🔵🔵🔵🔵🔵🔴🔴🔴🔴🔴🔴🔴
今後の取り込み
上記のツイスティパズルのソルバーをバックロジックとし、それにフロントエンドを加え可視化・可操作化をやりたいです。便利にパズルの定義、編集、自動解答、自動アルゴリズム発見など色々やってみたいです。
更に、いろんなユーザのパズルの発明、検証、アルゴリズム創造などの交流の場とする「puzzlehub」(githubのように)を実現したいと思います。興味を持っていただける有志者は一緒にやりませんか?
最後に
中学時代から3X3X3のルービックキューブからはじめ、そしていろんな似て非な異種のパズルを知り、近年は就職後は、収入自由に支配できるようになって、やったことのないものを好奇心の駆使でどんどん手に入れて、ついにコレクターになってしまいました。そして人間の頭で解けないパズルやゲームなどプログラミングで解決することに幸せの源泉になっています。
フューチャーで学んだIT技術と自分の知識や趣味を融合して、新たな創造を生み出すという精神を大事にしています。