はじめに
フューチャーAdventCalender2 2019の25日目(The last of this year!)です。
ちなみにアドベントカレンダー1の記事はこちらから。
今年で入社4年目になりますが、趣味はパズルとそれらを解くためのアルゴリズムです。
職場のデスク上には写真のような様々なルービックキューブを置いています。特に怒られることなく、好きなものに囲まれつつ自由な雰囲気の中で楽しく仕事ができています。
本題
一般な人は、「怖くて触りたくない」、もしくは、「一面だけ頑張って揃えられるが、それ以上は壊したくないので撤退する」といった方が少なくないと思います。
インターネットで調べたら、↓のようなルービックキューブの6面完全攻略法がいっぱい出てきます。
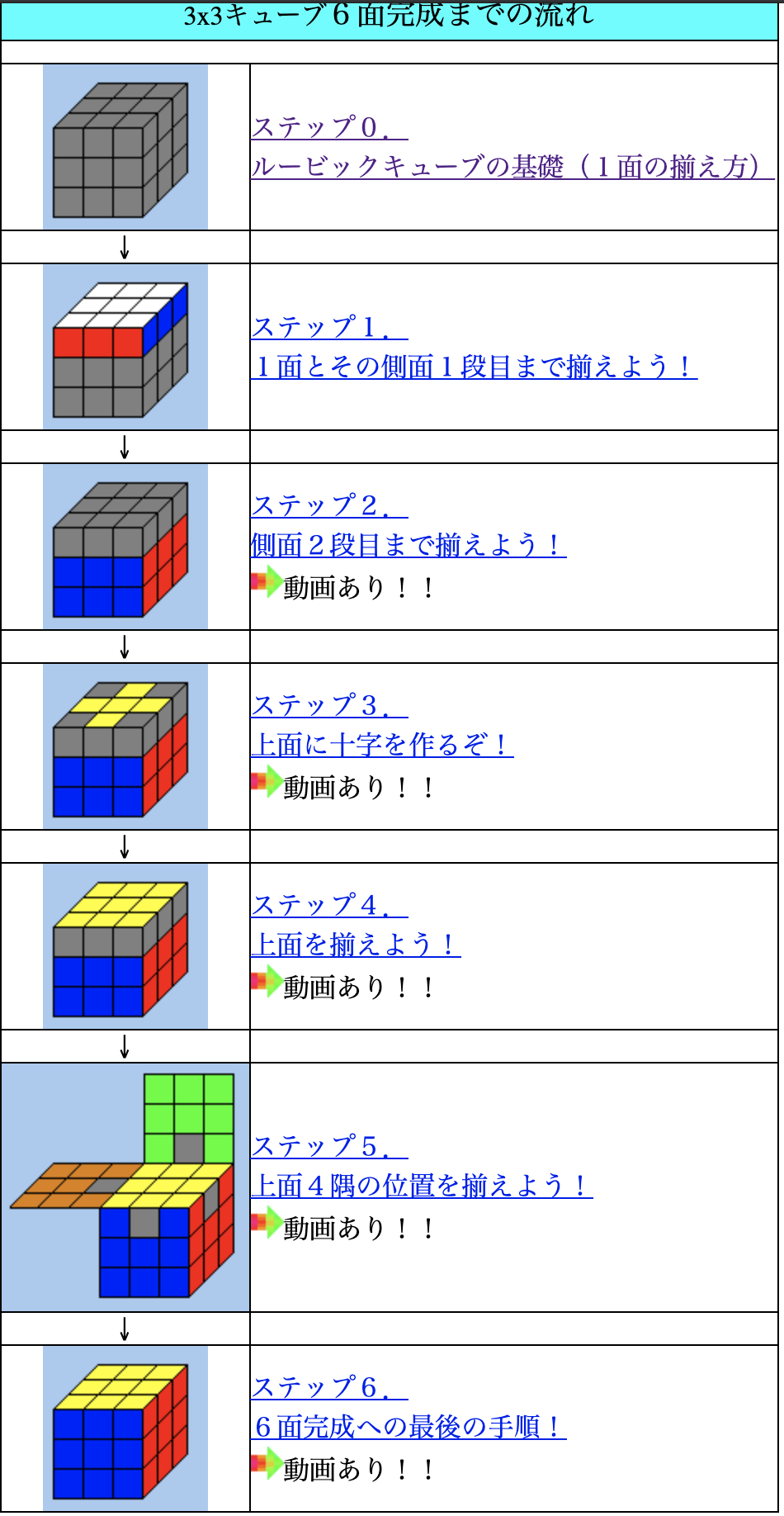[初心者向け解け方例](https://macozy.com/rubik/3rc/index.html)
それらを取扱説明書として片手にキューブを完成させ、「ウンウンできた」と満足することもいいでしょう。しかし私はそれをあまり推奨しません。理由は以下となります。
- あまりにも手順が煩雑すぎて、完全に理解するまで根気がなくなる
- それぞれステップかつそれぞれすごく多いパターン数かつそれぞれ長い手順、全然覚えられない
- 手順を見ながらなんとか6面揃えたとしても、全部のパターンに対して手順を覚えないと、独立に解けると言えない
- 手順を全部覚えきった人にとっても、なぜかその手順で揃えるのを理解しづらいので腑に落ちない
なので、本記事では、手順なしに汎用的なルービックキューブの揃え方を紹介します。しかも、その汎用性は、3x3x3のルービックキューブに限らなく、NxNxNまで適用できる簡単な方法を説明します。記憶より理解を重視する人への福音です。
この記事が説明しないこと
- スピード復元、もしくは、復元の最短経路を探索するアルゴリズム、その実装
- 覚えにくい複雑な復元アルゴリズム
- 変な形なルービックキューブ (例: 2x2x3 tower cube、megaminx など)
- ルービックキューブ以外のパズル (例: チャイニーズリング、[箱入り娘]
この記事が説明すること
- 具体的なケースバイケースのテクニックではなく、超汎用的にNxNxNルービックキューブに対する方法論
- 見た瞬間にすぐ覚える1個のシンプルな手わざの紹介
- その手わざを用いて、他のピースに影響のない前提で、同時に3つのピースの場所を交換する方法
- その手わざを用いて、他のピースに影響のない前提で、同時に2つのピースを向きを回転する方法
この記事を読むことで身につくこと
- 初めてルービックキューブを触る人でも、解き方の方向性が分かる
- 最速の解き方ではないけど、一番ベーシックの手わざを組み合わせてルービックキューブのどんな状況でも解ける(論理上)
- 3x3x3だけではなく、2x2x2や4x4x4及びそれ以上のハイレイヤーのルービックキューブでも解け方が分かる
- 自分なりの方法でルービックキューブを解く人にはヒントになり、できないケースでもこの方法を知っておくと安心
前提知識
- 説明の方便上、一般に使われている回転記号
FR2U'などを使う → こちらに参考してください - 各ピースが「位置」と「向き」は2種類の状態を持っている
- 他のパズルにもあるかもしれないが、ルービックキューブには、パリティ(ありえない状態)が存在します。有名なパリティは下図のように解けない15パズルがあります。 → [1] (14と15は論理上交換不可能)
ルービックキューブを壊さない限り、どうしても、ありえない状態(パリティ)の例を2個挙げます。
(デモの中に、三角のPlayボタン▶を押すと動的なデモが始まります)
パリティについての数学原理などは割愛しますが、ざっくりとルービックキューブの制約を以下にまとめます。
- 1色のセンターピース、2色のエッジピースと3色のコーナーピース、お互いに場所交換することが不可能
- 他のピースに影響しない前提で、単独にエッジピースとコーナーピースの向きを回転することが不可能
- ↑に対して、2個のピースA,Bは、同時に逆方向の向き回転(例、A時計回り、B反時計回り)なら可能
- 他のピースに影響しない前提で、2個のピースA,Bは、向きを変えずに場所のみ交換すること(A=>B=>A)が不可能
- ↑と同条件で3個のピースA,B,Cの場所交換(A=>B=>C=>A)なら可能
したがって、影響範囲が最も小さく、一番ベーシックな可能な操作は、ただ以下の2個あります。
- 3つピースA,B,Cの場所を交換する (順番例: A=>B=>C=>A)
- 2つのピースA,Bの向きを逆方向に回転する (例: A反時計回り、B時計回り)
ゴールドフィンガー (Gold Finger)
この手わざは僕の発明ではないですが、インターネットで検索してもなかなか出ないため、「ゴールドフィンガー(Gold Finger)」(以下略称GF)と命名しました。石を金に変えられる仙人の指というイメージで、万能的な技を表しています。
ゴールドフィンガーは、実はとても簡単(Simple is beautiful)です。見た瞬間、もう覚えられます。
さっそく見てみましょう。 → [デモ]
びっくりするほどシンプルでしょう。でも、「それですべてのルービックキューブを解ける？嘘でしょう!」と思われますが、急がば回れ、まずはGFの操作の性質を分析しましょう。
-
性質1.GFの逆動作はGF自身なので、GFは2回実施すると元に戻ります。 -> [デモ] -
性質2.GFは上の層の1ピース(上右前)を下の層(下左後)に持ってく効果があります。もう一回実行すると、戻ってきます。
性質1.からの推論は、GFを2回、もしくは、偶数回実施すると、全体は無変化になります。後ほどの説明で分かるが、それはとても優れている性質です。
性質2.の使い道を説明する前に、まずプログラミングの時、変数aとbの値交換(swap)のやり方を思い出してみてください。
func swap(a, b *int) {
var temp = *a
*a = *b
*b = temp
}
*本記事のソースコードはGolangの文法に準じます。
temp変数を臨時的な置き場として用いて、aとbを交換していますね。
では、今度は、a,b,cの3つの変数を順次に一個ずらして次の変数に値をシフトする問題を考えましょう。
要するに、b,c,a = a,b,cのような代入をやりたいです。しかし、ルービックキューブに適用するために、以下の制限も含めて考えてほしいです。
【制限】代入を使えなくて、swapしか使えません。
ちょっと考えたら、以下のように、a,b,c,aを順次にあるtempと交換すればいいですね。
func shift(a, b, c *int){
var temp
swap(a, &temp) // aの値を変数tempに入れる
swap(b, &temp) // 変数tempにあるaの値をbに入れる, bの値を変数tempに入れる
swap(c, &temp) // 変数tempにあるbの値をcに入れる, cの値を変数tempに入れる
swap(a, &temp) // 変数tempにあるcの値をaに入れる, aにある元々tempの値を変数tempに還元する
}
ちょっと脱線しましたが、本題に戻ります。GFの性質2.を活用したら、上層の上右前のコーナーピースAが下層のTempピースと交換し、退避されたイメージですね。
さて、例えば上層のコーナーピースA B Cを順次場所交換したいなら、4つのswap
A <=> Temp
B <=> Temp
C <=> Temp
A <=> Temp
を順次実行すればいいですね。ルービックキューブ言語に翻訳すると、A,B,C,Aに対して順次にGFを実行してあげればいいです。
ここまで読んだ方の中には、次の疑問を持つ方もいらっしゃるのではないでしょうか？
A,B,Cは順次に変えられますしTempも元の位置に戻れますが、他のピースはバラバラになりませんか？
答えは、大丈夫です。
GFの優れている性質1.を振り返りましょう。偶数回実行したら、元に戻ります!
実行時のコツは上層のA,B,C,Aに対してGFを実行する時、他の層の相対位置は変わらないことです。
言い換えると、GFを実行する前に、対象コーナーピースを同じ場所(例:上右前)に持ってこないといけません。
つまり、他のピースを影響しないで、上層のA,B,CをA=>B=>C=>A順番でシフトする時、以下のように実行すればいいです。
- Aを上右前に置く
-
GFを実行 - Bを上右前に置く
-
GFを実行 - Cを上右前に置く
-
GFを実行 - Aを上右前に置く
-
GFを実行
さて、効果を確認しましょう。 -> [デモ]
エッジピースにも活用
考え方は理解したら、同じ方法をエッジピースの場所交換にも簡単に展開できますね。
ちょっとだけ改造した(GF for Edge)略称GFE -> [デモ]
を使いかえたらOK！
ただ半周回す層を従来の下層から中間層に変えただけですね。(Simple is beautiful)
3x3x3 => NxNxN
Nが大きいほど難しいイメージですが、手順のステップ数は確かに増えますが、実は難しさは割と収まってそれ以上増えません。
前述のGFやGFEは汎用的な方法なので、全部適用できます。
9x9x9のコーナーピース場所交換 -> [デモ]
10x10x10のエッジピース場所交換 -> [デモ]
ピースの向きを回転
GFを用いて、3つのピースを向き変えずに場所交換することが確かにできますが、ピース向き回転をどうすればいいですかね。
前述までは右手の層でGFを実行しただけですが、実は、どの層で実行してもGFの基本性質は変わりません。
例えば、鏡に映ったように、前層でやるGF Mirrored(略称GFM)鏡像操作も前述のすべてのことができます。 -> [デモ]
回転の実現方法のポイントは、
GFで退避したピースをGFMで別方向から持って返せばいいです。
もちろん他のピースに影響しないように、もう一回順にGFMとGFを実行しなければなりません。
つまり、他のピースに影響しないで、上層のコーナーピースA,Bを向き回転(A反時計回り、B時計回り)する時、以下のように実行すればいいです。
- Aを上右前に置く
-
GFを実行してTempに退避する -
GFMを実行してTempから持って返す - Bを上右前に置く
-
GFMを実行 -
GFを実行
さて、効果を確認しましょう。 -> [デモ]
もちろん、エッジピースの向き回転も似たようなやり方で簡単にできます。それを割愛します。
また、上層のA,B,C配置によって、GFとGFMを使って場所交換と向き回転の二重効果を同時に得ることも可能です。興味があったら、ぜひチャレンジしてみてください。
結論
ルービックキューブは怖くありません。最も基本な場所交換と向き回転ができれば、それを組み合わせてNxNxNでも解けます。
複雑の問題を簡単化する方法論を念頭に置けば、どんな難問でも解ける自信を身に付けます。
僕はこれからもいろいろチャレンジし続けたいと思います。
最後に、メリークリスマス～ 良いお年を〜
