Python その2 Advent Calendar 2015の13日目の記事です。
普段の仕事として主に音響信号処理のアルゴリズム開発やDSP実装などを行っているのですが、アルゴリズムを構築する際は最初にPythonを使ってアルゴリズムの検討を行い、その結果を踏まえてCやC++でPC上で動作するリアルタイムモデルを作成するという流れで行っています。音響信号処理に関するまとまった日本語記事は意外に存在しないため、ここではPythonで音響信号処理を行う方法およびこれまでに仕事等で使って来たノウハウなどを適当にまとめようと思います。
目次
- Pythonで音響信号処理をするモチベーション
- オーディオファイルの読み書き
- リアルタイムにオーディオ処理を行いたい
- 周波数応答を表示したい
- デジタルフィルタを設計したい
- 零点、極と係数配列b, aを変換したい
- デジタルフィルタを時系列信号に適用したい
- 群遅延を計算したい
- 時間相関(相互相関関数)を計算したい
- ピークを検出したい
Pythonで音響信号処理をするモチベーション
matlabの代替です。
matlabは商用利用の場合20万以上するため固定資産扱いとなり、扱いが厄介であったりそもそも会社に買ってもらえなかったりするため無料でなんとかしたいというのが正直なところです。
オーディオファイルの読み書き
オーディオファイルの読み書きの方法は、過去にはてなブログに書いたpythonでwavファイルを扱う108の方法の記事にまとめています。個人的には最近はPySoundFileを使うことが多くなってきました。
以下は1/2オーバーラップでFFTしてIFFTして元に戻すだけの処理です。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import numpy as np
import scipy.fftpack as fft
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
# wavファイル読み込み
filename = sys.argv[1]
wav, fs = sf.read(filename)
# ステレオ2chの場合、LchとRchに分割
wav_l = wav[:, 0]
wav_r = wav[:, 1]
# 入力をモノラル化
xs = (0.5 * wav_l) + (0.5 * wav_r)
n_len = len(xs)
n_fft = 128
n_overlap = 2
n_shift = n_fft / n_overlap
# 中間バッファ
zs = np.zeros(n_len)
Zs = np.zeros(n_fft)
# 出力バッファ
ys = np.zeros(n_len)
# 窓関数
window = np.hanning(n_fft)
# FFT & IFFT
for start in range(0, n_len - n_shift, n_shift):
xs_cut = xs[start: start + n_fft]
xs_win = xs_cut * window
Xs = fft.fft(xs_win, n_fft)
# some signal processing
Zs = Xs
zs = fft.ifft(Zs, n_fft)
# write output buffer
ys[start: start + n_fft] += np.real(zs)
# 冒頭から10秒分プロット
fig = plt.figure(1, figsize=(8, 10))
ax = fig.add_subplot(211)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(212)
ax.plot(ys[:fs*10])
ax.set_title("output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
plt.show()
リアルタイムにオーディオ処理を行いたい
PortAudioのPythonバインディングであるPyAudioを使うのが楽です。
ここではマイク入力信号をコールバックメソッド内でグローバル変数にバッファリングして、wavファイルに保存する例を挙げます。
まず使用可能なデバイスを列挙します。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import pyaudio as pa
if __name__ == "__main__":
# 使用可能なデバイスを列挙
p_in = pa.PyAudio()
print "device num: {0}".format(p_in.get_device_count())
for i in range(p_in.get_device_count()):
print p_in.get_device_info_by_index(i)
$ python pyaudio_print_devices.py
device num: 2
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.01, 'defaultLowInputLatency': 0.00199546485260771, 'maxInputChannels': 2L, 'structVersion': 2L, 'hostApi': 0L, 'index': 0, 'defaultHighOutputLatency': 0.1, 'maxOutputChannels': 0L, 'name': u'Built-in Microph', 'defaultHighInputLatency': 0.012154195011337868}
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.004693877551020408, 'defaultLowInputLatency': 0.01, 'maxInputChannels': 0L, 'structVersion': 2L, 'hostApi': 0L, 'index': 1, 'defaultHighOutputLatency': 0.014852607709750568, 'maxOutputChannels': 2L, 'name': u'Built-in Output', 'defaultHighInputLatency': 0.1}
"maxInputChannels"を見ると最初のデバイスが2Lとなっており、"name"がu'Built-in Microph'となっているためこちらが入力デバイスとなっていることが分かります。
次にマイク入力をwavファイルに保存するスクリプトです。PyAudioにはコールバックを用いたnon-blockingな処理方法と、コールバックを用いないblockingな処理方法がありますが、ここでは前者のコールバックを用いる方法で処理します。コールバックメソッドの中で入力信号をshortから-1.0〜1.0のfloatに変換し、グローバル変数のxsにひたすら結合します。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import time
import numpy as np
import soundfile as sf
import pyaudio as pa
# global
xs = np.array([])
def callback(in_data, frame_count, time_info, status):
global xs
in_float = np.frombuffer(in_data, dtype=np.int16).astype(np.float)
in_float[in_float > 0.0] /= float(2**15 - 1)
in_float[in_float <= 0.0] /= float(2**15)
xs = np.r_[xs, in_float]
return (in_data, pa.paContinue)
if __name__ == "__main__":
# pyaudio
p_in = pa.PyAudio()
py_format = p_in.get_format_from_width(2)
fs = 16000
channels = 1
chunk = 1024
use_device_index = 0
# 入力ストリームを作成
in_stream = p_in.open(format=py_format,
channels=channels,
rate=fs,
input=True,
frames_per_buffer=chunk,
input_device_index=use_device_index,
stream_callback=callback)
in_stream.start_stream()
# input loop
# 何か入力したら終了
while in_stream.is_active():
c = raw_input()
if c:
break
time.sleep(0.1)
else:
in_stream.stop_stream()
in_stream.close()
# 入力信号を保存
sf.write("./pyaudio_output.wav", xs, fs)
p_in.terminate()
これを実行し、何か入力するとwhileループから脱出して"./pyaudio_output.wav"にxsを保存します。
なおp_inをopenする時にinput=Trueとする代わりにoutput=Trueとすると再生デバイスとして扱われます。詳しくはPyAudioのページ下部のサンプルを見ると良いです。
周波数応答を表示したい
scipy.signalにfreqzという周波数応答を求めるメソッドがありますが、この記事で書いたように多項式をnp.polyvalで求めている部分が重く、連続して実行するとその遅さが如実に目立ちます。従って先の記事でも書いたように、scipy.fftpackを用いる下記のようなメソッドを定義して周波数応答を求めることができます。
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N+1] / fft.fft(a, 2 * N)[:N+1]
return w, h
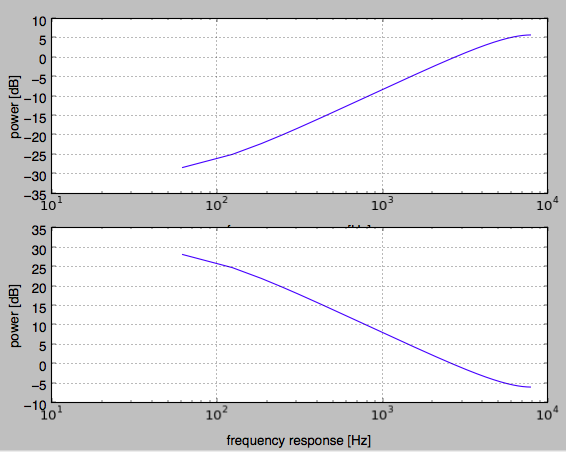
たとえば単純なエンファシス(高域強調)フィルタb=[1.0, -0.97]およびその特性を元に戻すデエンファシスフィルタb=[1.0], a = [1.0, -0.97]の応答を求めることとすると、以下のようなスクリプトによって周波数応答をそれぞれプロットできます。wの範囲は0〜πであるため、プロットする時の横軸は0〜FS/2となることに注意が必要です。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == "__main__":
plt.close("all")
N = 1024
FS = 16000.0
EMP = -0.97
b_emp = [1.0, EMP]
a_emp = [1.0]
b_deemp = [1.0]
a_deemp = [1.0, EMP]
(w_emp, h_emp) = my_freqz(b_emp, a_emp, worN=N)
(w_deemp, h_deemp) = my_freqz(b_deemp, a_deemp, worN=N)
fig = plt.figure(1)
ax = fig.add_subplot(2, 1, 1)
ax.semilogx(w_emp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_emp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
ax = fig.add_subplot(2, 1, 2)
ax.semilogx(w_deemp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_deemp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
plt.show()
これにより下記のような応答がプロットされます。
デジタルフィルタを設計したい
scipy.signalには種々のフィルタ設計関数が用意されており、FIRフィルタ設計関数(firwin, firwin2, remezなど)やmatlab互換のIIR設計関数(butter, buttord, cheby1, cheb1ordなど)が用意されています。
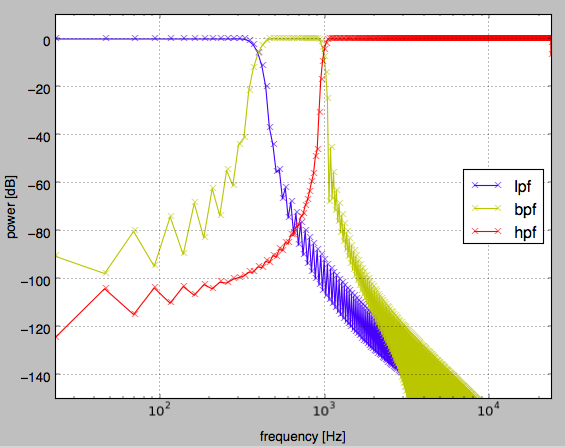
例えばfirwinを使ってLPF、BPF、HPFを求めるには下記のようなスクリプトで可能です。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sg
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == '__main__':
plt.close("all")
fs = 48000.0
num_tap = 1024
lpf_cutoff_hz = 400.0
hpf_cutoff_hz = 1000.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
bpf_band = np.array([lpf_cutoff_hz, hpf_cutoff_hz]) / (fs/2.0)
hpf_cutoff = hpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
bpf = sg.firwin(num_tap, bpf_band, pass_zero=False, window=win)
hpf = sg.firwin(num_tap, [hpf_cutoff, 0.9999], pass_zero=False, window=win)
# plot filter response
w, lpf_h = my_freqz(lpf, worN=num_tap)
w, bpf_h = my_freqz(bpf, worN=num_tap)
w, hpf_h = my_freqz(hpf, worN=num_tap)
lpf_amp = np.abs(lpf_h)
bpf_amp = np.abs(bpf_h)
hpf_amp = np.abs(hpf_h)
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(lpf_amp), "bx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(bpf_amp), "yx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(hpf_amp), "rx-")
ax.set_xlim([0.0, 24000.0])
ax.set_ylim([-150.0, 10.0])
ax.set_ylabel("power [dB]")
ax.set_xlabel("frequency [Hz]")
ax.grid()
ax.legend(["lpf", "bpf", "hpf"], loc="best")
plt.show()
また、biquad型(2次IIR)のフィルタを設計したい場合はEQ Cookbookに従って関数を自作しています。例えば、ピーキングEQの場合は下記のような感じです(返り値はb, a)。
def peaking_eq(q, gain, f, fs):
A = 10 ** (gain / 40.0)
w0 = 2.0 * np.pi * f / fs
alpha = np.sin(w0) / (2.0 * q)
b = [(1.0 + alpha * A), (-2.0 * np.cos(w0)), (1.0 - alpha * A)]
a = [(1.0 + alpha / A), (-2.0 * np.cos(w0)), (1.0 - alpha / A)]
return (np.array(b) / a[0]), (np.array(a) / a[0])
零点、極と係数配列b, aを変換したい
tf2zpkやzpk2tfを用います。tfはtime filter, zpkはzero, pole, k(gain)のことです。6次IIRのフィルタなどを作った際にそのままCで実装すると誤差で発散することがあるため、零点と極が分かればフィルタを2次IIRのフィルタ3段に分解する、といったことが可能となります。
デジタルフィルタを時系列信号に適用したい
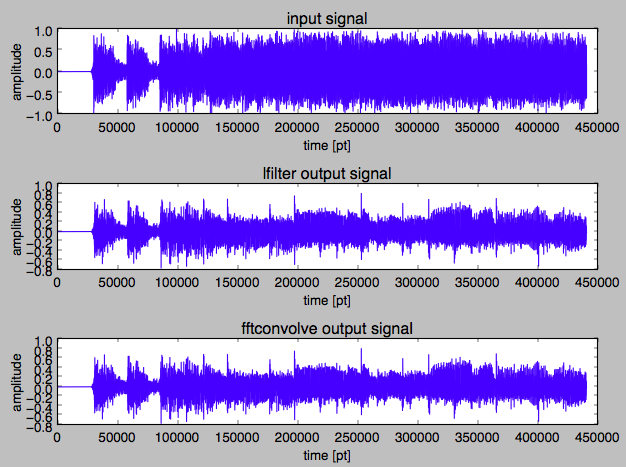
設計したデジタルフィルタを時系列信号に適用する方法は主に2つあります。時間領域での畳み込みを用いる方法ではscipy.signal.lfilterを、フィルタの畳み込みを周波数領域での瞬時処理として処理するためにはscipy.signal.fftconvolveを用います。下記にlpfを入力にそれぞれのメソッドを用いて適用した結果をプロットするスクリプトを記載します。
# !/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import scipy.signal as sg
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
# wavファイル読み込み
filename = sys.argv[1]
wav, fs = sf.read(filename)
# ステレオ2chの場合、LchとRchに分割
wav_l = wav[:, 0]
wav_r = wav[:, 1]
# 入力をモノラル化
xs = (0.5 * wav_l) + (0.5 * wav_r)
# LPF設計
num_tap = 1024
lpf_cutoff_hz = 400.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
# 線形フィルタ適用
ys = sg.lfilter(lpf, [1.0], xs)
# 周波数領域フィルタ適用
zs = sg.fftconvolve(xs, lpf, mode="same")
# 冒頭から10秒分プロット
fig = plt.figure(1)
ax = fig.add_subplot(311)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(312)
ax.plot(ys[:fs*10])
ax.set_title("lfilter output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(313)
ax.plot(ys[:fs*10])
ax.set_title("fftconvolve output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
fig.set_tight_layout(True)
plt.show()
群遅延を計算したい
振幅を変えず位相のみを変化させるフィルタであるオールパスフィルタの特性を見る場合、特に群遅延を求めることで周波数ごとのサンプル単位遅延がどれだけあるかを把握することができます。しかしscipy.signalにはmatlabに存在するgrpdelay関数が存在しないため、適当な方法で自力でgrpdelayを実装する必要があります。そこでここでは各周波数による微分を1次差分に基づく近似で求める方法を紹介します。
def grpdelay(w, h, fs):
"""単純な1次近似による群遅延特性の計算(結果はサンプル単位)。差分で計算するため次元が一つ減るので必ず最後の要素は0にしている。wは正規化周波数、hはwに対応する周波数特性"""
return -1.0 * np.r_[np.diff(np.unwrap(np.angle(h))) / np.diff(w), [0]]
matlabのgrpdelayで用いられているアルゴリズムとは厳密には異なりますが、ざっくりした結果を見るだけであればこれで十分です。
時間相関(相互相関関数)を計算したい
scipy.signalにはmatlabなどで言うところのxcorrが存在しません。xcorrはウィーナヒンチンの定理に基づいて周波数領域上でクロススペクトルを求め逆変換によって相互相関関数を求めるため、時間領域で積和算を行うよりも高速に相互相関関数を求めることができます。
以下では時間領域で相互相関関数を求めるmy_correlateメソッドに対応したxcorrメソッドを定義しています。
ceil2は引数と同じかそれよりも大きい2の累乗の値を探すメソッドで、引数が2の累乗であればx & (x - 1)が0になるため引数の値を返し、そうでない場合は引数を2進数表記の文字列に直して、文字列処理で最上位ビット以外を0とし、その数字を1ビット左シフトさせた値を求めています。
def my_correlate(sig, ref, lag=None):
lag = np.alen(ref) / 2 if lag is None else lag
corrs = []
sig_len = np.alen(sig)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_expand = np.r_[np.zeros(lag), sig, np.zeros(lag)]
center = lag
for begin in range(center - lag, center + lag + 1):
sig_cut = sig_expand[begin :begin + sig_len]
corrs.append(np.dot(sig_cut, ref))
return np.array(corrs) / (sig_norm * ref_norm)
def ceil2(x):
new_x = 0
if (x & (x - 1)) == 0:
new_x = x
else:
bit_str = bin(x)
head_bit = bit_str[2]
tail_bits = bit_str[3:].replace("1", "0")
new_bit_str = "0b" + head_bit + tail_bits
new_x = int(new_bit_str, 2) << 1
return new_x
def xcorr(sig, ref, lag=None):
import scipy.fftpack as fft
lag = 1024 if lag is None else lag
sig_len = np.alen(sig)
nfft = ceil2(sig_len)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_ = sig / sig_norm
ref_ = ref / ref_norm
X = fft.fft(sig_, nfft)
Y = fft.fft(ref_, nfft)
# ifft to calculate correlation
corr_p = np.real(fft.ifft(X * np.conjugate(Y), nfft))
corr_m = np.real(fft.ifft(Y * np.conjugate(X), nfft))
# concat
corr = np.r_[corr_m[1:lag+1][::-1], corr_p[:lag+1]]
return corr
実際はFFTを用いる場合は巡回の影響を考えなければならないので、上記は改善の余地があるような気もします。
参考: http://www.ikko.k.hosei.ac.jp/~matlab/xcorr.pdf
ピークを検出したい
scipy.signalにもfind_peaks_cwtというメソッドがありますが、もっと簡便で軽い関数が欲しかったので以下のようなメソッドを使っています。
def find_peaks(a, amp_thre, local_width=1, min_peak_distance=1):
"""
閾値と極大・極小を判定する窓幅、ピーク間最小距離を与えて配列からピークを検出する。
内部的にはピーク間距離は正負で区別して算出されるため、近接した正負のピークは検出される。
:rtype (int, float)
:return tuple (ndarray of peak indices, ndarray of peak value)
"""
# generate candidate indices to limit by threthold
idxs = np.where(np.abs(a) > amp_thre)[0]
# extend array to decide local maxima/minimum
idxs_with_offset = idxs + local_width
a_extend = np.r_[[a[0]] * local_width, a, [a[-1]] * local_width]
last_pos_peak_idx = 0
last_neg_peak_idx = 0
result_idxs = []
for i in idxs_with_offset:
is_local_maximum = (a_extend[i] >= 0 and
a_extend[i] >= np.max(a_extend[i - local_width: i + local_width + 1]))
is_local_minimum = (a_extend[i] < 0 and
a_extend[i] <= np.min(a_extend[i - local_width: i + local_width + 1]))
if (is_local_maximum or is_local_minimum):
if is_local_minimum:
if i - last_pos_peak_idx > min_peak_distance:
result_idxs.append(i)
last_pos_peak_idx = i
else:
if i - last_neg_peak_idx > min_peak_distance:
result_idxs.append(i)
last_neg_peak_idx = i
result_idxs = np.array(result_idxs) - local_width
return (result_idxs, a[result_idxs])
以上
他にも書きたいことがあるような気がしますが以上です。
次回は@kimihiro_nさんです。