本記事は以下の記事の続編です。未読の方はこちらを先に読むことをオススメします。
はじめに
本記事では、前回の記事で紹介した双対性1の見方(原則)を発展させて、より一般化された形での捉え方について説明します。実を言うと、前回説明した原則1「点と線の双対性」は、「点」と「線」のそれぞれの空間の次元数が一致する特殊ケースのみを説明していました。しかし機械学習や数理最適化の文脈でよく見かける主問題・双対問題では、一般的に両者の次元数が異なります。例えば機械学習のカーネル法では、主問題が無限次元、双対問題がサンプル数次元であり、まさにこのケースに当たります。このような状況を幾何学的に捉えるには、前回の特殊ケースからもう一段階イメージを広げる必要があります。
今回は、線形計画法などで登場する線形制約(超平面や半空間の共通部分)を例に挙げ、数式との関連性をより明確にしながら、次元数が異なる場合へと一般化した原則について解説します。後半で原則を可視化したGIFアニメを用意していますので、先にそちらを眺めると読むモチベーションが湧くかもしれません。
原則1': 点と線の双対性(次元数が異なる場合)
ある2次元平面($x_1x_2$平面)上にある以下の2つの「直線」について考えます。
a_{11} x_1 + a_{12} x_2 = b_1, ~~~
a_{21} x_1 + a_{22} x_2 = b_2,
これらの方程式を適当な重み $\lambda_1, \lambda_2$ を掛けて足すと次式が得られます。
(\lambda_1 a_{11} + \lambda_2 a_{21}) x_1 + (\lambda_1 a_{12} + \lambda_2 a_{22}) x_2 = \lambda_1 b_1 + \lambda_2 b_2
ここで左辺の各係数と右辺をそれぞれ $\bar a_1, \bar a_2, \bar b$ とすれば、これもまた直線の方程式 $\bar{a}_1 x_1 + \bar{a}_2 x_2 = \bar{b}$ の形ですから、この式も $x_1x_2$ 平面上の何がしかの直線を表します。2
次にこの見方を $n$ 次元空間($\boldsymbol{x}$空間)上にある $m$ 個の「超平面」へと一般化しましょう。
\langle\boldsymbol{a}_1,\boldsymbol{x}\rangle = b_1, ~~~
\langle\boldsymbol{a}_2,\boldsymbol{x}\rangle = b_2, ~~~
\ldots, ~~~
\langle\boldsymbol{a}_m,\boldsymbol{x}\rangle = b_m \tag{1}
なお $\langle\cdot,\cdot\rangle$ は2つの縦ベクトル間の内積です。先ほどと同じ要領で、これらの各方程式に重み $\lambda_1,\lambda_2,\ldots,\lambda_m$ を掛けて足すとこうなります。
\langle \lambda_1\boldsymbol{a}_1+\lambda_2\boldsymbol{a}_2+\cdots+\lambda_m\boldsymbol{a}_m, \boldsymbol{x} \rangle = \lambda_1 b_1 + \lambda_2 b_2 + \cdots + \lambda_m b_m \tag{2}
ここで、左辺の係数ベクトルを $\bar{\boldsymbol{a}}$ 、右辺を $\bar{b}$ とすれば、これはまさに超平面の方程式 $\langle\bar{\boldsymbol{a}},\boldsymbol{x}\rangle = \bar{b}$ ですから、この式も $\boldsymbol{x}$ 空間中の何がしかの超平面を表しています。
さて、これらの式を行列を使ってより簡潔に記述しましょう。新たに $\boldsymbol{A} := [\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_m]^\top\in\mathbb{R}^{m \times n}$, $\boldsymbol{b} := [b_1,b_2,\ldots,b_m]^\top\in\mathbb{R}^{m}$ および $\boldsymbol{\lambda} := [\lambda_1,\lambda_2,\ldots,\lambda_m]^\top\in\mathbb{R}^{m}$ を定義します。すると、 (1) の $m$ 個全ての超平面の方程式はまとめて
\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b} \tag{3}
と書けますが、これは全ての超平面が交わる部分(=共通部分)を表します。また (2) の重みつき和の超平面の方程式は次式のように書けます。
\langle\boldsymbol{A}^\top\boldsymbol{\lambda},\boldsymbol{x}\rangle = \langle\boldsymbol{b},\boldsymbol{\lambda}\rangle \tag{4}
この式は (3) の両辺に左から $\boldsymbol{\lambda}^\top$ を掛けることでも得られます。誤解しやすいので念押ししますが、一見すると単一の式に見える (3) は実際には $m$ 個の式をまとめた記述であり、複数の超平面の共通部分を表します。一方の (4) は単一の条件式(両辺それぞれスカラ値なので)であり一つの超平面を表します。
というわけで、ここで(バレバレの)伏線を回収しますが、この重みベクトル $\boldsymbol{\lambda}$ こそがいわゆる「双対変数」と呼ばれるものです。何かしら $\boldsymbol{\lambda}$ を適当に定めると、(4) は $\boldsymbol{x}$ 空間中の何かしらの超平面を表しますよね。つまり、この式をブリッジとして、$\boldsymbol{\lambda}$ 空間中の「点」が $\boldsymbol{x}$ 空間中の「超平面」に対応します(ただし異なる $\boldsymbol{\lambda}$ が同じ超平面を表す場合もあり得ます)。このイメージは前回の原則1と共通ですが、間に $\boldsymbol{A}$ を挟むことで、$\boldsymbol{x}$ と $\boldsymbol{\lambda}$ の次元数が異なる形となります。
実は双対問題というのは、$\boldsymbol{\lambda}$ を通じて $\boldsymbol{x}$ 空間中の超平面を動かすことで問題を解こうとしています。なんとなくウルトラハンド越しに物を掴もうとするような回りくどさを感じますが、逆にこれによって主問題よりも性質や見通しがよくなる場合があるのです。先ほど例に挙げたカーネル法であれば、 $\boldsymbol{x}$ よりも $\boldsymbol{\lambda}$ のほうが低次元であるという事実が計算の効率化に寄与しています。まさに双対性の面白いところです。
原則2': 半空間の共通部分とその数学表現
次に、前回はイメージを定性的に説明するにとどまっていた原則2をより数学的に整理しましょう。上述の原則1'での議論は、等号を不等号に変えることで「超平面」から「半空間」へと自然に拡張できます。ただし重要な注意点として、新たに不等号の向きを気にする必要がでてきます3。これも凸最適化等でよく登場する条件なので丁寧に見ていきましょう。
先ほどと同じ要領で、$n$ 次元空間($\boldsymbol{x}$空間)上にある $m$ 個の「半空間」を考えます。単に「超平面」の式 (1) を不等号 $\leq$ に変えただけです。
\langle\boldsymbol{a}_1,\boldsymbol{x}\rangle \leq b_1, ~~~
\langle\boldsymbol{a}_2,\boldsymbol{x}\rangle \leq b_2, ~~~
\ldots, ~~~
\langle\boldsymbol{a}_m,\boldsymbol{x}\rangle \leq b_m \tag{5}
これら $m$ 個の不等式を (3) と同じようにまとめて記述しましょう。なお、ベクトル間の不等号はベクトルの各要素毎に適用するものとします。
\boldsymbol{A}\boldsymbol{x} \leq \boldsymbol{b} \tag{6}
この条件を満たす $\boldsymbol{x}$ は $m$ 個全ての半空間が重なった部分(=共通部分)に属します。これはまさに前回の原則2の捉え方ですね。同様に (4) も機械的に不等号に変えれば
\langle\boldsymbol{A}^\top\boldsymbol{\lambda},\boldsymbol{x}\rangle \leq \langle\boldsymbol{b},\boldsymbol{\lambda}\rangle \tag{7}
となります。この式も $\boldsymbol{x}$ 空間中の何がしかの半空間を表しています。ここまでは超平面(等号)でのお話しと同様の流れです。不等号でもまた、点 $\boldsymbol{\lambda}$ が $\boldsymbol{x}$ 空間中のある半空間と対応するわけです。
ところがどっこい!、半空間(不等号)のケースにおいて一つ重要なポイントがあります。式(7) を次のように変形しましょう。
0 \leq \langle\boldsymbol{\lambda},\boldsymbol{b}-\boldsymbol{A}\boldsymbol{x}\rangle
式(6) を満足する $\boldsymbol{x}$ (つまり $m$ 個の半空間の共通部分)では常に $\boldsymbol{b}-\boldsymbol{A}\boldsymbol{x}\geq\boldsymbol{0}$ が成り立ちますので、双対変数を $\boldsymbol{\lambda}\geq\boldsymbol{0}$ に限定すれば上式は常に成り立ちます。つまり、(7) で表される半空間が「 $m$ 個の半空間の共通部分全体」を含むことが保証されます。これは前回の原則2そのものであり、双対変数を介してハンドリングする半空間が所望の領域全体を含んでおいてほしい、という意図を実現します。この双対変数の非負値条件 $\boldsymbol{\lambda}\geq\boldsymbol{0}$ は最適化の多くの場面で登場しますが、その裏にはこういった意図が隠れていたのでした。
原則の図解
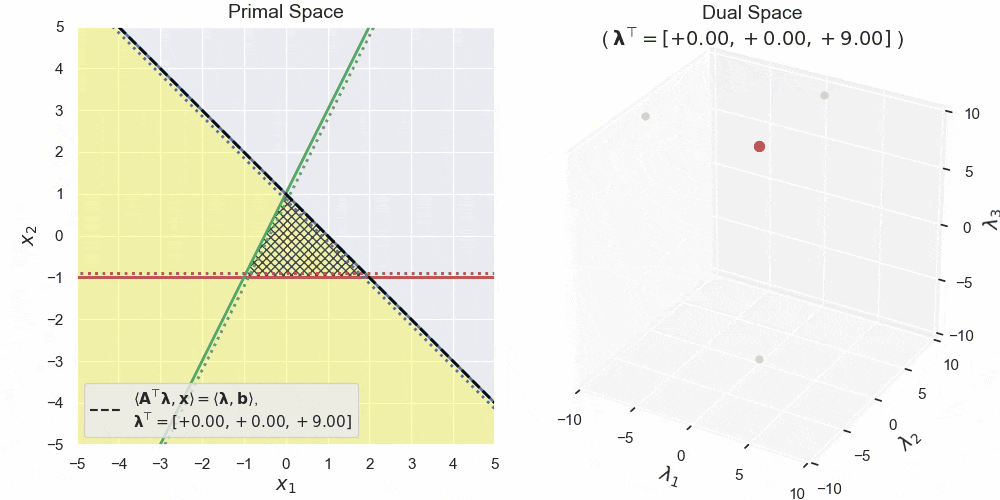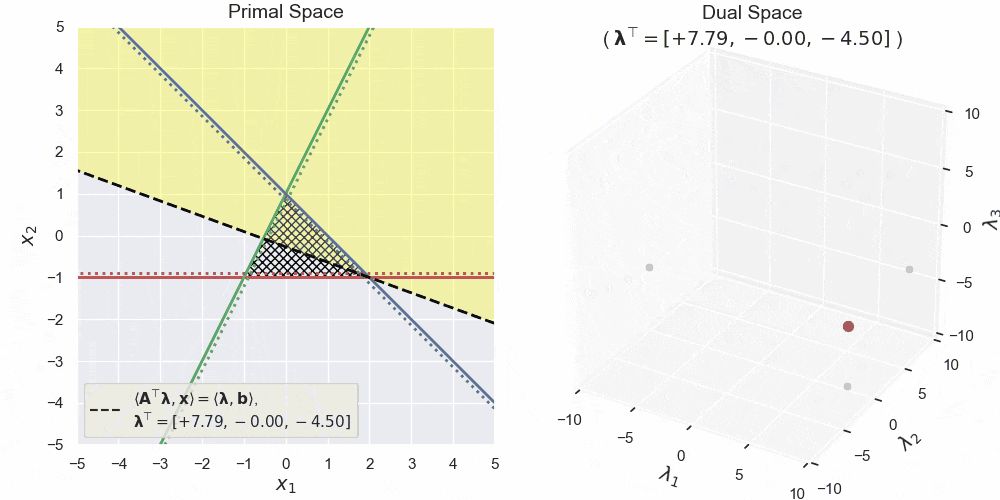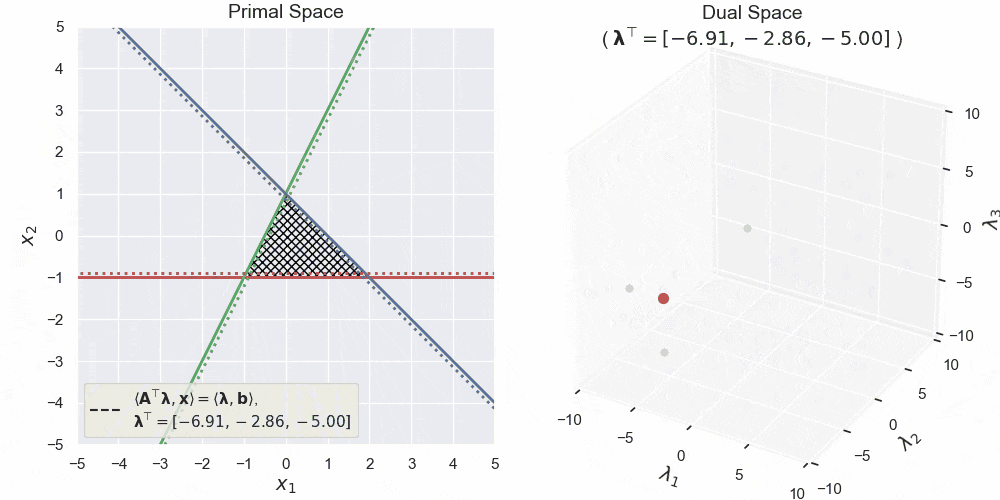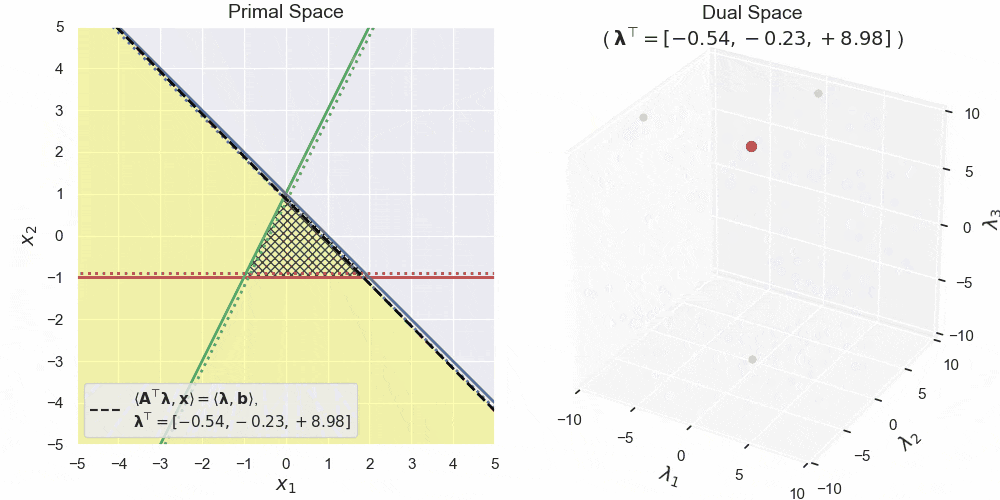
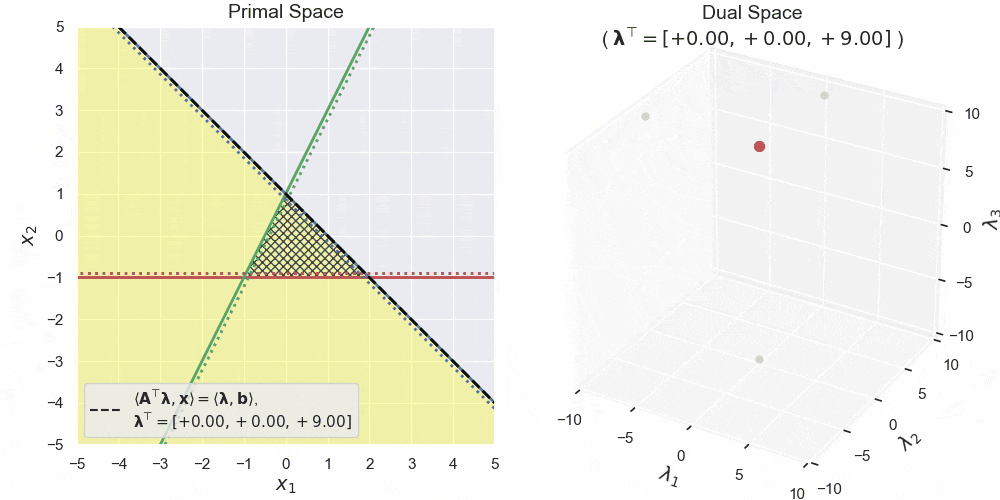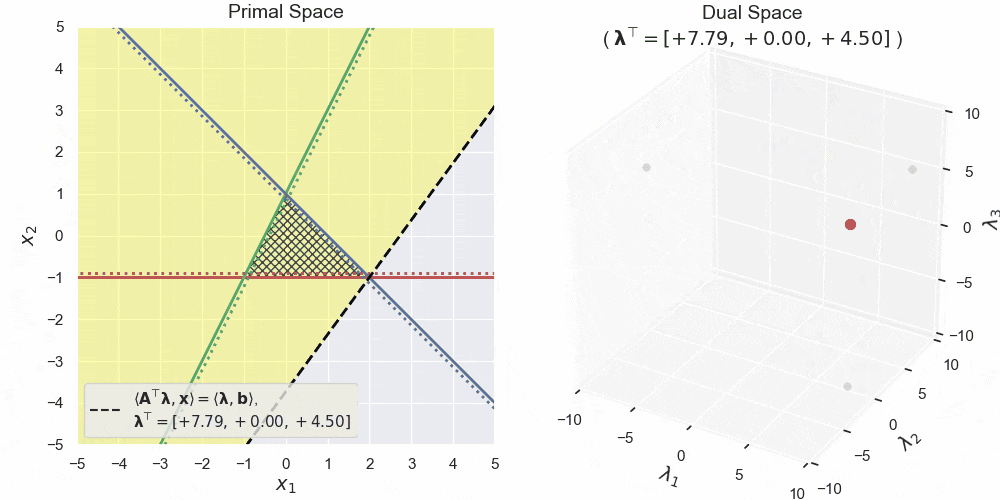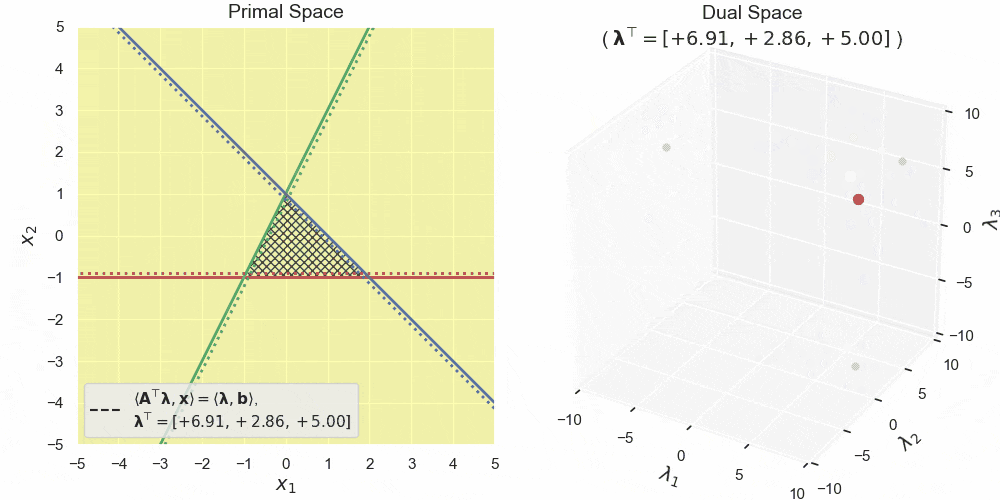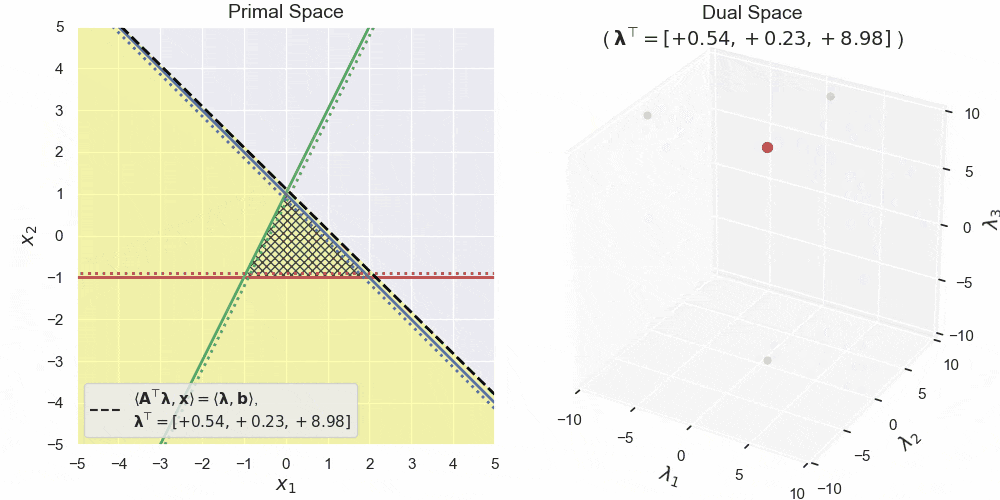
言葉や数式だけではピンとこないと思いますので、実例を挙げて例のごとくアニメでお見せします。主変数 $\boldsymbol{x}$ の空間は2次元とし、その上に3つの半空間を作ります。よって双対変数 $\boldsymbol{\lambda}$ の空間は3次元となります。3つの半空間は次のように定義します。
\boldsymbol{A} := \begin{bmatrix} 0 & -1 \\ -2 & 1 \\ 1 & 1 \end{bmatrix}, ~~~
\boldsymbol{b} := \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix},
また、適当な言葉がないため、主変数の空間を「主空間 (primal space)」、双対変数の空間を「双対空間 (dual space)」と便宜上呼ぶことにします。これらは私の造語であって一般的なものではありませんのでご注意ください。では見ていきましょう!
左図が主空間、右図が双対空間です。主空間における赤・青・緑の直線が3つの半空間の境界線を表します。三角形の網掛け領域はそれらの共通部分 $\boldsymbol{A}\boldsymbol{x} \leq \boldsymbol{b}$ です。黄色領域は双対変数 $\boldsymbol{\lambda}$ によって形作られる半空間 $\langle\boldsymbol{A}^\top\boldsymbol{\lambda},\boldsymbol{x}\rangle \leq \langle\boldsymbol{b},\boldsymbol{\lambda}\rangle$ で、特にその境界線を黒の破線で表しています。見ての通り、双対空間中の点と主空間中の半空間が対応しており、双対変数がグリグリ動くと、それにあわせて主空間中の半空間もグリグリ動いている様子が確認できます。
さらに双対変数の非負値条件 $\boldsymbol{\lambda}\geq\boldsymbol{0}$ を加えてグリグリ動かしたものが上図になります。見てもらうと、主空間の黄色領域が常に網掛け領域全体を含んでいることがわかります。このような半空間の共通部分をとればこの網掛け領域そのものになりますが、それはつまり前回の記事の原則2の捉え方そのものなわけです。
おわりに
前回の説明した原則を拡張しより数学的に明確な記述にしてまとめました。この見方がピンとくると、線形計画法の双対問題の意図も幾何学的に捉えられるようになるでしょう(次回のネタ)。これを知ったところで最適化をガシガシ解けるようになるなんてことはないのですが、なんだかよくわからない数式を眺めて勉強するよりはスッキリした気持ちで勉強できるのではないかと思います。
本記事は今から2年近く前にがんばって書いていたのですが、そのあと転職・転居x2と日々の子育てで時間的・精神的に余裕がなく、お蔵入りになりそうだったところを気合で修正して、なんとか当初の前半部だけ公開できました。書きかけの後半部も近いうちに公開・・・できるといいなぁ。いずれはこの方針で Lagrangeの未定乗数法 とか KKT条件 あたりのイメージも明快に説明できると思っているので、それもまたどこかのタイミングでまとめたいと思います。ぜひ気長にお待ちいただければと思います。