これまで少しづつ書き進めていた記事を、せっかくなので「数理最適化 Advent Calendar 2020」の一つとして公開することにしました。
はじめに
最適化を勉強すると「双対」という言葉をよく見かけます。例えば、学部生であれば線形計画法の単元で「双対問題」を学ぶでしょうし、機械学習であればサポートベクターマシンを解く際に突然「双対問題」を導出し解いたりします。最適化の論文を読むと「主双対なんちゃら」のような名前の方法が登場します。この「双対」という言葉、たくさん出てきますが、一体何をやっているのか、皆さんイメージ湧きますか? 僕は全く湧きませんでした。授業や専門書に触れても「これが双対問題です!」と天下り的に式が示されることばかりでしたし、もう少し丁寧な説明でもLagrange双対(あるいはFenchel双対)の定義が示されて、それを適当な主問題に適用して対応する双対問題を導出する、といった感じでしょうか。正直、式の導出手順は覚えられても、なんだかスッキリ理解できた気分にはなりません。なぜなら、「そのトリッキーに見える事実に行きついたキッカケ」のようなものが示されていないからです。無から唐突に(有益とされる)概念が登場した感じがしませんか?(・・・しない方はページをココでそっ閉じしましょう)
本記事では、この双対のイメージを幾何学的に説明してみます。より正確に言うと、最適化で頻出するLagrange双対(Fenchel双対も実はこれとかなり似たもの)の最初のアイデアや動機を順を追って紐解きます。最適化の文脈で「双対」といった場合、ほぼほぼLagrange双対(かその変形のFenchel双対)だと思って大丈夫です。このイメージがつかめたからと言って、急に双対問題の導出が得意に!?なったりは残念ながらしませんが、凸解析の序盤に出てくる様々な概念をすんなり受け入れやすくはなるはずです。私がここ4年くらい勉強して色々調べて整理したお話しですが、大学院での講義でもこのテーマについては学生の反応も上々だと思います。なお、数学用語については厳密でない点が多々ありますが、文章の簡潔さを優先しています。大目に見てもらえるか、優しくフォローしてもらえると嬉しいです。
双対の概念を構成する2つの原則
まずはじめに、おそらく感覚的に受け入れやすいであろう2つの数学的アイデア(原則1,2と呼びます)について示します。この二つが適当に組み合わさることで、多くの凸解析の概念や定理がある程度直観的に理解できます。
原則1: 点と線の双対性
下の図を見てください。まず左図の横軸 $x$、縦軸 $y$ からなる $xy$ 平面を考えましょう。この平面上のある一点は $(x,y)$ と表せます。また同平面上のある一次関数は $y=ax-b$ と定式化できます(この後の話を美しくするために、あえて切片を $-b$ として定義しています)。この一次関数は傾きと切片を用いて特徴づけられるので、簡潔に $\lceil a,b \rfloor$ と記述しましょう。ポイントは、$xy$ 平面上において、$(x,y)$ は点、$\lceil a,b \rfloor$ は線(一次関数)を描くということです。次に右図の、横軸 $a$、縦軸 $b$ からなる $ab$ 平面を考えましょう。この平面上のある一点は $(a,b)$ と表せ、同平面上の一次関数は $b=xa-y$ と定式化できるので、線は傾きと切片を用いて $\lceil x,y \rfloor$ と表せます。ここからわかる重要なポイントは、関係式 $y+b=ax$ をブリッジとして、互いの平面上での点と線の立場が入れ替わって表現されている事実です。これを便宜上「点と線の双対性」と呼びましょう(これは私の造語で正式名称があるのかわかりません)。
【2021/07/05追記】下図の青点の位置は誤りです。正しくは $(+2,+1)$ です。
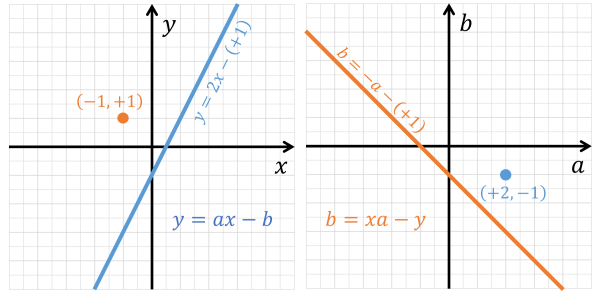
この2次元平面の例は容易に多次元に拡張できます。多次元の場合には先ほどの一次関数 $y=ax-b$ を一般化した超平面の方程式 $y=\langle\boldsymbol{a},\boldsymbol{x}\rangle-b$ を通じて考えます。同じアプローチで、$\boldsymbol{x}y$ 空間中のある点 $(\boldsymbol{x},y)$ とある超平面 $\lceil\boldsymbol{a},b\rfloor$ は、$\boldsymbol{a}b$ 空間では超平面 $\lceil\boldsymbol{x},y\rfloor$ と点 $(\boldsymbol{a},b)$ としてそれぞれ表現されます。要するに、両者をつなぐ関係式が $y+b=\langle\boldsymbol{a},\boldsymbol{x}\rangle$ へと一般化されただけです。面倒なので、この場合でも単純に「点と線の双対性」と呼びましょう。
面白いことに、互いに「見え」が交換されただけでなく、交点と交線の立場も入れ替わっていたり、点と線の間の縦軸方向の距離が保存されたりといった性質も同時に成り立ちます。
原則2: 集合を半空間の共通部分として表す
厳密にいえば閉凸集合ですが、厳密な表現はちゃんとした文献に譲りまして、ここでは下図を使ってラフなイメージを説明します。ある集合を幾何学的にイメージするとき、おそらくほとんどの方はそれを左側のような「点の集合」として捉えているかと思います。例えば、ある二次元の単位円の内部として表される集合であれば、条件 $x^2+y^2 \leq 1$ を満たす $(x,y)$ を無数に集めたようなイメージです。
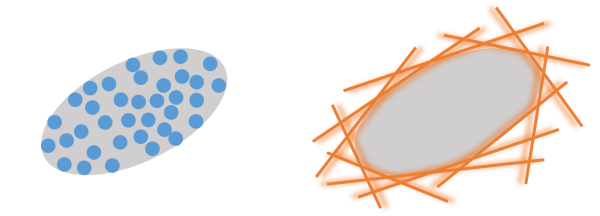
で、実は凸解析では、これとは異なる集合の表現方法を考えたりします(ただし、この事実を丁寧に説明した資料はかなり少ないです)。それは集合を右側の図のように「半空間の共通部分」という形で表現する方法です。例えて言うと、ケーキを作るために四角いスポンジケーキから丸い形を抜き出しますが、このときナイフで余分な箇所を取り除くことを繰り返して丸い形を抽出しますよね。これと同じ要領で、余分な箇所を半空間を使ってカットしていき、残った部分が所望の集合になっている、というような表現手段をとります。もちろん、半空間は無限に長いナイフですから、いわゆる集合の凹み部分については表現できません。したがって、厳密に表現できるのは凸集合に限られ、非凸集合ではその凸包の表現に限られます。
さて、このトリッキーな表現手段では、凸集合は「半空間の集合」となるわけですが、半空間を表す不等号の向きを統一すれば、各半空間をその境界面の情報だけで特徴づけられます。2次元で言えばそれはすなわち境界線の集合であり、その境界線とはまさに接線であり、結局のところ「線の集合」に帰着できるわけです。ここまで来ると、先ほどの原則1との絡みが見えてきたのではないかと思います。
原則から紐解く凸解析の基礎
原則2によって凸集合は「線の集合」にコンバートできますが、この各線に対して原則1の「点と線の双対性」を適用すれば、結局のところ元々の素朴な「点の集合」とは別物の「点の集合」に帰着します。基本的に双対の世界で見えているものはこれにあたります。様々な場面でこの解釈あるいはその応用が効いてくるのですが、紙面と手間の都合がありますので、ここではある程度簡潔に説明できる部分だけ解説してみます。
共役関数: 原則2の凸関数版に原則1した
共役関数は次式で表されます。本では $\boldsymbol{a}$ が傾きで~やらなんちゃら説明していますが、だいたい何を言っているのかわからないです。
f^\star(\boldsymbol{a}) := \sup_{\boldsymbol{x}} \left\{ \langle\boldsymbol{a},\boldsymbol{x}\rangle - f(\boldsymbol{x}) \right\} = -\inf_{\boldsymbol{x}} \left\{ f(\boldsymbol{x}) - \langle\boldsymbol{a},\boldsymbol{x}\rangle \right\}
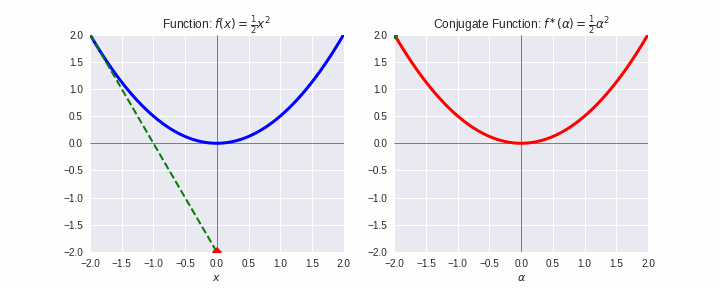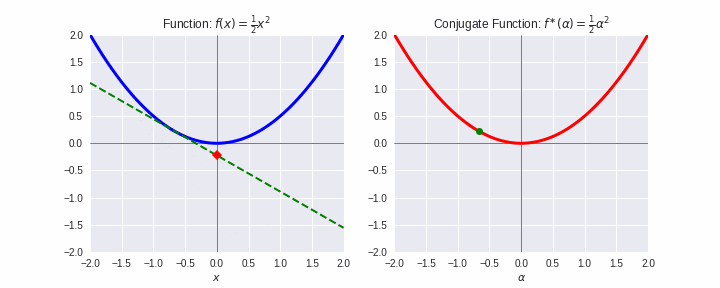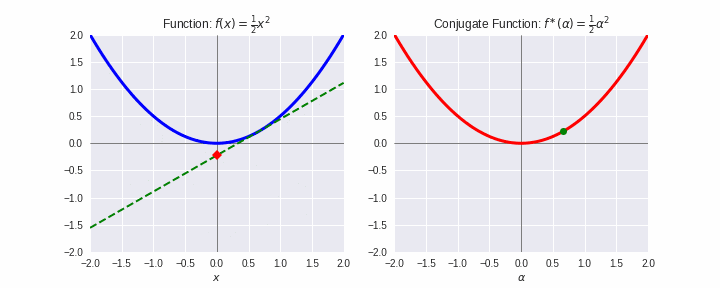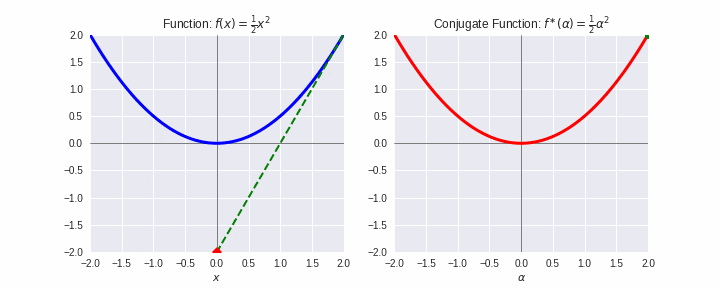
例として、二次関数とその共役関数を下図に示しました。凸関数のエピグラフ(関数より上側のゾーン)は凸集合です。これに対して原則2を適用しましょう。これは左側のように関数に対して下から定規(ここでは緑の線)をあてて滑らせるような動作になります。この緑の線を原則1で双対の世界にもっていった軌跡が右側であり、凸解析で「共役関数」と言われているものです。あぁースッキリ!(笑顔)
前に書いた記事もあわせて読むと、いくつか他のパターンも紹介してますのでより理解しやすいでしょう。
Fenchel-Youngの不等式: 主と双対の世界の間のブリッジ式を少し変形
Fenchel-Youngの不等式は $\langle\boldsymbol{x},\boldsymbol{a}\rangle \leq f(\boldsymbol{x}) + f^\star(\boldsymbol{a})$ という式ですが、原則1における主と双対の世界の間のブリッジとなる式 $\langle\boldsymbol{a},\boldsymbol{x}\rangle = y+b$ と本質的なところはだいたい同じです。既にすんなりわかるかと思いますが、$y$ と $b$ は各世界における切片ですし、$f(\boldsymbol{x})$ と $f^\star(\boldsymbol{a})$ も同様に各世界における縦方向の高さに関連しています。共役関数の定義に上界の操作が含まれるので不等号になっています。
線形計画の双対問題: 原則2による接線から目的関数の等高線と平行なもの探し
本当はこれを詳細に説明したかったのですが、図を作るまでの時間と労力が足りませんでしたので、また別の記事としてまとめます。
線形計画問題では制約集合が凸集合です。図がなくて恐縮ですが、この集合に対して外から定規をあてて初めて接する点を探しているのが双対問題になります。この定規の向きは主問題の目的関数の等高線と平行である必要があるため、それを双対問題では制約条件として課しています。これも原則2を使って解釈するならば、順番が逆にはなりますが、制約集合を「接線の集合」にコンバートした上で、その中で目的関数の等高線と平行のものを探すことと等価です。
弱双対性・強双対性
原則2では凹みを表現できない話をしました。これが弱・強双対性の違いにつながります。対象が凸であれば、厳密に双対の世界にもっていくことができ、逆に同様の操作で主の世界に戻すことができます。凹みがないため、最適点に対して必ず接線をあてることができます。これが強双対性が成り立つ状況です。一方、集合に凹みがあると、最適点がその凹みの部分に入りこむ可能性が残るため、不等式の形にせざるをえません。これがいわゆる弱双対性となります。かなりざっくりした説明ですが、基本的に双対は接線をあてる動作がベースにあるので、「凹みに対して非力」ということを覚えておくと色々納得しやすいかもです。
おわりに
ここ4年くらいずっと考えてまとまった知識を、最後のほうかなり適当ですが、とりあえず書いてみました。これがわかったところで難しいことができるようになるわけではないですが、凸最適化の基礎で出てくる数式の行間を多少埋めることができていたら本望です。他にも、例えばLagrange関数がこの原則と絡んでくるところとかも書きたいのですが、それはまた別の機会にまとめてみます。最後まで読んでいただきありがとうございました!