Udemy - ゼロからPythonで学ぶ人工知能と機械学習 : ニューラルネットワークまとめ

みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習

ネットワークに関するセッションの全体に対する自分用まとめ。

ニューロンクラス

• ネットワークを構成する各ノードとなるニューロンの定義。
• 入出力はN:1の関係となる。入力は複数だが出力は常に一つ。（ただし出力の行き先がひとつとは限らない）

class Neuron:
    input_sum = 0.0  # 最終的にこの値が少しずつ増える
    output = 0.0  # output用

    def setInput(self, inp):
        self.input_sum += inp

    def getOutput(self):
        self.output = sigmoid(self.input_sum)
        return self.output

    # input/output values intialize
    def reset(self):
        self.input_sum = 0
        self.output = 0

ニューラルネットワーククラス

• 複数のニューロンから構成されるニューラルネットワークの定義。
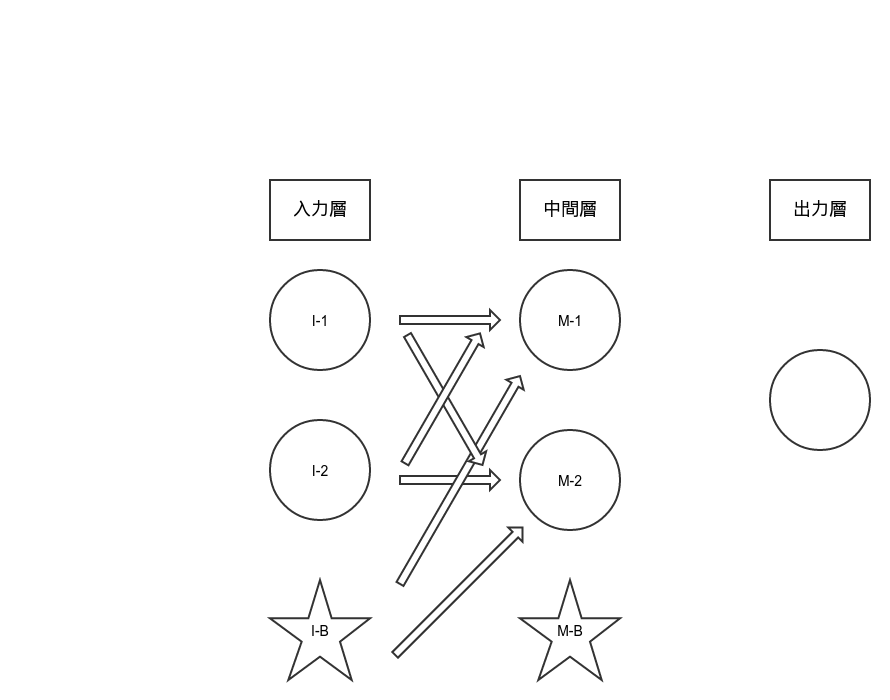
• w_imは入力層の３ノード（ニューロン・ニューロン・バイアス）からの中間層各ノードへ入る際の重み。w_moは同じく中間層→出力層の各重み。
• C言語風に書くなら、各層間の重みの数w_im[x][y]はx = 入力ノードの数/y = 出力先ノードの数となる。
  • この場合、入力元はニューロン・ニューロン・バイアスの３つ、出力先は（バイアスは独立しているので）ニューロン・ニューロンの２つ。合計３*２で重みは６個定義される。
• 定義されるノード数は３+３+１個。
  • 入力層ニューロンの出力初期値は0, 0で固定。また、バイアスも1.0で固定。

class NeuralNetwork:
    # 入力値の重みづけ
    # 入力層・中間層間の重み
    w_im = [[0.496, 0.512], [-0.501, 0.998], [0.498, -0.502]]  # 第一入力NEU→各中間NEUの重み, 第二入力NEU→各中間NEUの重み, 入力バイアス→各中間NEUの重み
    # 中間層・出力層間の重み
    w_mo = [0.121, -0.4996, 0.200]  # 第一中間NEU→出力NEUの重み, 第二中間NEU→出力NEUの重み, 中間バイアス→出力NEUの重み

    # 各層宣言
    # 入力層：N（ニューロン）、N、バイアス　入力層は数値がそのまま入る
    input_layer = [0.0, 0.0, 1.0]
    # 中間層：Nインスタンス、Nインスタンス、バイアス
    middle_layer = [Neuron(), Neuron(), 1.0]
    # Nはひとつだけ
    output_layer = Neuron()

コミット関数

• 入力された２値(今回の場合はinput_data[0/1]が入力の緯度経度)・各重みからネットワーク全体の出力(＝出力ノードの出力値)を得る。
• 中間層第一ニューロンへの入力は入力層各ノードの出力値に対応した各重みを乗じたものの合算になる。(今回の構成の場合はニューロン・ニューロン・バイアスから３値の合計)
• バイアスの出力値は変わらない。(ただしバイアスからの入力値は重みによって変わりうる)

    # Receive inputs,
    def commit(self, input_data):
        # 各層ニューロン初期化
        self.input_layer[0] = input_data[0]
        self.input_layer[1] = input_data[1]
        self.middle_layer[0].reset()
        self.middle_layer[1].reset()
        self.output_layer.reset()

        # 入力層→中間層
        # 第一中間ニューロンに入力３つ
        nr_idx = 0
        self.middle_layer[nr_idx].setInput(self.input_layer[0] * self.w_im[0][nr_idx])  # 第一入力N出力値×対応重み
        self.middle_layer[nr_idx].setInput(self.input_layer[1] * self.w_im[1][nr_idx])
        self.middle_layer[nr_idx].setInput(self.input_layer[2] * self.w_im[2][nr_idx])  # バイアス

        # 第二中間ニューロンに入力３つ
        nr_idx = 1
        self.middle_layer[nr_idx].setInput(self.input_layer[0] * self.w_im[0][nr_idx])
        self.middle_layer[nr_idx].setInput(self.input_layer[1] * self.w_im[1][nr_idx])
        self.middle_layer[nr_idx].setInput(self.input_layer[2] * self.w_im[2][nr_idx])  # バイアス

        # 中間層→出力層
        self.output_layer.setInput(self.middle_layer[0].getOutput() * self.w_mo[0])
        self.output_layer.setInput(self.middle_layer[1].getOutput() * self.w_mo[1])
        self.output_layer.setInput(self.middle_layer[2] * self.w_mo[2])  # バイアス

        return self.output_layer.getOutput()  # ニューラルネットワーク全体の出力値が帰る

学習関数

• 学習関数∋コミット関数となるため、最終的にはコミット関数は呼び出さず、学習関数を呼び出すことでネットワークを使用する。
• 細かい部分は後で再度動画を見て確認する必要があるが、とにかく「一度ネットワークの出力値を得た後、出力値と正解値の差分」から中間層→出力層間の重みを修正、さらに「変更前の中出重・変更後の中出重から入中重を修正」する。
• 関数下部のself.w_im[n][m]６つが冒頭の概要図における「矢印６つ」に対応している。

    def learn(self, input_data):
        # 出力値 コミットに緯度と経度を渡す ニューラルネットワークの出力値が帰る
        output_data = self.commit([input_data[0], input_data[1]])
        # 学習する correct_valueに0/1で正解/不正解
        correct_value = input_data[2]

        # print output_data
        # print (correct_value - output_data) # 出力/正解値の誤差

        # δmo = (出力値 - 正解値) * 出力の微分: 入力層・中間層修正にも使う
        # 差分が小さい／大きいときは修正量が小さくなる、真ん中ぐらいだと大きくなる
        # 中間層ー出力層：修正量 = δmo * 中間層の値 * 学習係数(定数：大きすぎると重みの値が発散する、小さすぎると時間がかかる)

        # 学習係数(定数)
        K = 0.3

        # 出力層→中間層
        # 差分 * (微分値) ※シグモイド関数による微分は「n * (1 - n)」になる。
        delta_w_mo = (correct_value - output_data) * output_data * (1.0 - output_data)
        # 変更前重み
        old_w_mo = list(self.w_mo)

        # 重み更新 中間層出力値 * δ * 固定係数
        self.w_mo[0] += self.middle_layer[0].output * delta_w_mo * K
        self.w_mo[1] += self.middle_layer[1].output * delta_w_mo * K
        self.w_mo[2] += self.middle_layer[2] * delta_w_mo * K # バイアス

        # δim = δmo * 中間出力の重み * 中間層微分値
        # 入力層ー中間層：修正量 = δim * 入力層の値 * 学習係数

        # 中間→入力層
        delta_w_im = [
            delta_w_mo * old_w_mo[0] * self.middle_layer[0].output * (1.0 - self.middle_layer[0].output),
            delta_w_mo * old_w_mo[1] * self.middle_layer[1].output * (1.0 - self.middle_layer[1].output),
        ]

        # 重み更新 中間数はニューロン２つ　入力層はバイアス+ニューロンで３つ
        self.w_im[0][0] += self.input_layer[0] * delta_w_im[0] * K # I1-M1
        self.w_im[0][1] += self.input_layer[0] * delta_w_im[1] * K # I1-M2
        self.w_im[1][0] += self.input_layer[1] * delta_w_im[0] * K # I2-M1
        self.w_im[1][1] += self.input_layer[1] * delta_w_im[1] * K # I2-M2
        self.w_im[2][0] += self.input_layer[2] * delta_w_im[0] * K # IB-M1
        self.w_im[2][1] += self.input_layer[2] * delta_w_im[1] * K # IB-M2
        # I1 = 入力層第一ニューロン M1 = 中間層第一ニューロン IB = 入力層バイアス

メイン処理

• ファイルから↓みたいな感じのデータを読み込む。(緯度,経度,正解値(0/1))

training_data.txt

35.37,138.08,0
35.4,138.4,0
35.08,138.05,1
35.14,138.23,0
35.26,137.84,1
:
:

• ニューラルネットワークのインスタンスを生成した後、1000*100回試行する。
• 最終的な学習結果の重み付けをprintしている。

# 基準点(データの範囲を0.0〜1.0内に収める為)
refer_point_0 = 34.5
refer_point_1 = 137.5

# Read data
i = 0
training_data = []
training_data_file = open("training_data.txt", "r")
for line in training_data_file:
    i += 1
    line = line.rstrip().split(",")  # 改行を取り除き,で分ける
    training_data.append([float(line[0]) - refer_point_0, float(line[1]) - refer_point_1, int(line[2])])
training_data_file.close()

# print training_data

# Create NeuralNework instance
neural_network = NeuralNetwork()

# 学習（一度のみ）
# neural_network.learn(training_data[0])

# 学習（繰り返し）
for t in range (0, 1000) : # 1000回学習
    ii = 0

    for data in training_data : # 各データに対し実施（100回）

        if ((t % 100 == 0) and (ii == 0 or ii == 1)):
            print t, ":",
            print neural_network.w_im,
            print neural_network.w_mo

        ii += 1
        neural_network.learn(data) # t * 100回学習

print neural_network.w_im
print neural_network.w_mo

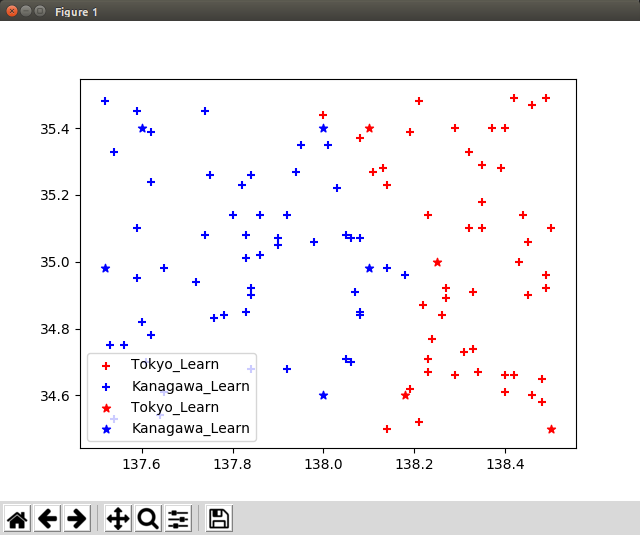
訓練用データ・実データのプロット

• 勘違いor読み飛ばししている可能性もあるけど、上の学習と関係ないよねこのあたりのコード。
• テキストから読み込んだデータを分類する。また、実際の緯度経度も同じグラフに描画する。
• ひと通り受講が終わったらこのあたりももう一度確認する必要があるか。

# 訓練用データ表示の準備
position_tokyo_leaning = [[], []]
position_kanagawa_leaning = [[], []]
for data in training_data:
    if data[2] < 0.5:  # 正解値が0.5以下（＝0）である場合
        position_tokyo_leaning[0].append(data[1] + refer_point_1)  # 経度
        position_tokyo_leaning[1].append(data[0] + refer_point_0)  # 緯度
    else:
        position_kanagawa_leaning[0].append(data[1] + refer_point_1)
        position_kanagawa_leaning[1].append(data[0] + refer_point_0)

# 実データで実行（答え合わせ）
data_to_commit = [[34.6, 138.0], [34.6, 138.18], [35.4, 138.0], [34.98, 138.1], [35.0, 138.25], [35.4, 137.6], [34.98, 137.52], [34.5, 138.5], [35.4, 138.1]]
for data in data_to_commit : # 緯度経度を0-1の中に収める
    data[0] -= refer_point_0
    data[1] -= refer_point_1

# 分類したデータを格納する
position_tokyo_learned = [[], []]
position_kanagawa_learned = [[], []]

for data in data_to_commit:
    if neural_network.commit(data) < 0.5 :
        position_tokyo_learned[0].append(data[1] + refer_point_1)
        position_tokyo_learned[1].append(data[0] + refer_point_0)
    else:
        position_kanagawa_learned[0].append(data[1] + refer_point_1)
        position_kanagawa_learned[1].append(data[0] + refer_point_0)


plt.scatter(position_tokyo_leaning[0], position_tokyo_leaning[1], c="red", label="Tokyo_Learn", marker="+")
plt.scatter(position_kanagawa_leaning[0], position_kanagawa_leaning[1], c="blue", label="Kanagawa_Learn", marker="+")

# 分類データ
plt.scatter(position_tokyo_learned[0], position_tokyo_learned[1], c="red", label="Tokyo_Learn", marker="*")
plt.scatter(position_kanagawa_learned[0], position_kanagawa_learned[1], c="blue", label="Kanagawa_Learn", marker="*")

plt.legend()
plt.show()