Matlabを使用した2自由度制御系の設計方法を紹介します。また,2自由度制御系のフィードフォワード制御手法として,東京大学 藤本博志先生の提案されている完全追従制御の紹介もします。
制御工学 Advent Calender 2019にて同日公開予定の記事とペアとなっています。こちらにて2自由度制御系のフィードバック制御の紹介しています。
外乱オブザーバの紹介
https://qiita.com/wcrvt/private/073d0256ccdac423c2fe
制御の自由度
はじめに古典制御の方式で書かれたブロック線図を用いて制御の自由度について説明します。下図は1自由度制御系と呼ばれるものです。
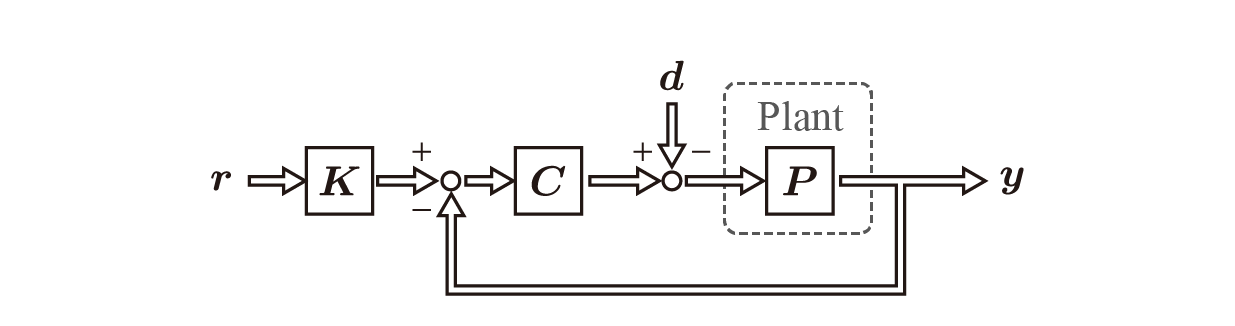
$r$は指令値,$y$は出力応答,$d$は外乱,$K$は指令値整形器,$C$はフィードバック制御器,$P$はプラントです。この制御系に出力は
y=(I+PC)^{-1}PCKr+(I+PC)^{-1}Pd
となります。指令値からの伝達関数と外乱からの伝達関数が等しい特性多項式$(I+PC)$を持ち,同じ極配置を持つことがわかります。B.A. Francisによって提唱された内部モデル原理に基づけば,外乱抑圧の条件は制御系が外乱生成多項式と等しい極を持つこととなります。例えば,ステップ外乱の生成には外乱生成多項式が原点に極を持つため,制御器も原点に極を持つ積分器を持つことが要求されます。振動抑制で見られるResonant Controllerもこの原理に基づくものです。ここで,制御器が積分器などを持つことにより,指令値-出力伝達関数に零点が発生したり特性方程式が高次となり,追従性能が劣化します。このように,外乱抑圧に重きを置いた場合には指令値追従特性が劣化するといったトレードオフが存在します。また,追従特性を上げようと制御ゲインを上げたとしても,制御器が外乱生成多項式と等しい極を持たない場合には,外乱は完全には抑圧されません。定常偏差が有名な例です。したがって,一つの特性のみしか満足に設計できないため,1自由度制御系と呼ばれています。
参考文献:
B. A. Francis and W. M. Wonham, The internal model principle of control theory, Automatica, Vol. 12, No. 5, pp. 457-465, 1976.
内部モデル原理の簡単な説明:
https://github.com/wcrvt/Textbook/blob/master/Control_20.pdf
そして,下図が2自由度制御系と呼ばれるものです。
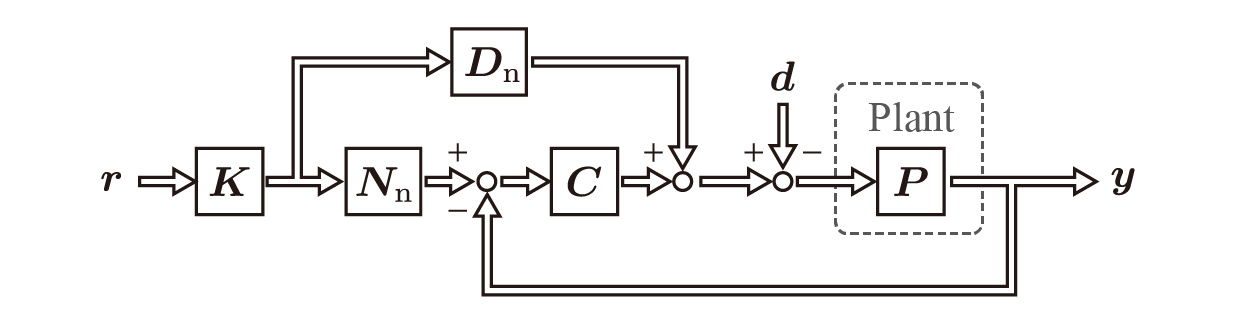
1自由度制御系と比較して,ループが追加されています。$N$,$D$はプラント$P$に既約表現における分子多項式と分母多項式となります$(P=ND^{-1})$。追加されたループはフィードフォワードループと呼ばれるもので,プラントの特性が予め分かっているのであれば,それに基づいて信号を入力すれば良いという考えです。この制御系の出力は
\begin{align}
y&=(I+PC)^{-1}PCNKr+(I+PC)^{-1}PDKr+(I+PC)^{-1}Pd\\
&=(I+PC)^{-1}(PCN+PD)Kr+(I+PC)^{-1}Pd\\
&=(I+PC)^{-1}(PC+PDN^{-1})NKr+(I+PC)^{-1}Pd\\
&=NKr+(I+PC)^{-1}Pd
\end{align}
となります。フィードフォワードループの働きにより,指令値追従特性と外乱抑圧特性が独立して設計できるようになっています。そのため,2自由度制御系と呼ばれます。良いフィードフォワード制御系を作ることが高速かつ精密な位置決めを実現し,フィードバック制御系が不確かさを抑制して動作の再現性を確保する働きがあります。実際には,モデル化誤差やシステム雑音がフィードバック制御系の性能を制限したりするので,制御性能の向上にはまだ多くの制御自由度が必要だったりします。現在では2自由度制御系を用いたロバスト制御理論の枠組み,例えば混合感度問題のようなものが使用されている例を見ます。
フィードフォワード制御系の設計
プラントモデルを得た際に,サンプル点で指令値に追従させる方法が完全追従制御です。ここからは状態空間表現を用いて議論します。次の連続時間状態空間表現について考えます。
\dot{x}(t)=Ax(t)+Bu(t)\\
y(t)=Cx(t)
$x$は状態,$y$は観測値,$u$は入力です。$A$,$B$,$C$は状態(遷移)行列,入力行列,観測行列と呼ばれます。$A$は状態$x$の自由運動を表すパラメータ,Bは入力$u$の影響度を表すパラメータとなります。これをサンプル値制御に適した形にするため,離散化を行います。次のような形式の状態空間表現に変形することを目指します。
x[k+1]=A_dx[k]+B_du[k]\\
y[k]=C_dx[k]
$k$はサンプルです。まず,連続時間状態空間表現の微分方程式を解いて時間応答を求めます。
x(t)=e^{At}x_0+\int^t_0 e^{A(t-\tau)}Bu(\tau) d\tau
ここで,$x_0$は状態量の初期値を表します。右辺第一項は初期値に対する自由運動を表し,第二項の畳み込み積分はインパルス応答の蓄積値を表す。$T_s$をサンプリング時間として,任意サンプル時刻$kT_{\rm s}$と次回サンプリング時刻$(k+1)T_{\rm s}$の状態の関係は以下のようになります。
\begin{align}
x((k+1)T_{\rm s})&=e^{A(k+1)T_{\rm s}}x_0+\int^{(k+1)T_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau\\
&=e^{AT_{\rm s}}e^{AkT_{\rm s}}x_0+e^{AT_{\rm s}}\int^{(k+1)T_{\rm s}}_{kT_{\rm s}} e^{A(kT_{\rm s}-\tau)}Bu(\tau) d\tau + \int^{kT_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau\\
&=e^{AT_{\rm s}}x(kT_{\rm s})+\int^{kT_{\rm s}}_0 e^{A((k+1)T_{\rm s}-\tau)}Bu(\tau) d\tau
\end{align}
ここで,入力$u$が区間内一定であるとすると,次式のように変形できます。これはデジタル制御系によくある制約です。
x((k+1)T_{\rm s})=e^{AT_{\rm s}}x(kT_{\rm s})+\int^{(k+1)T_{\rm s}}_{kT_{\rm s}} e^{A((k+1)T_{\rm s}-\tau)} d\tau Bu(kT_{\rm s})
また,積分計算において変数$\gamma=-\tau+(k+1)T_{\rm s}$を導入することで,次式を得ます。
x((k+1)T_{\rm s})=e^{AT_{\rm s}}x(kT_{\rm s})+\int^0_{T_{\rm s}}e^{A\gamma} (-d\gamma) Bu(kT_{\rm s})\\
=e^{AT_{\rm s}}x(kT_{\rm s})+\int^{T_{\rm s}}_{0} e^{A\gamma} d\gamma Bu(kT_{\rm s})
ここで,時刻$kT_{\rm s}$における状態および入力を$x[k],\ u[k]$と書くと,離散時間状態空間表現のパラメータは次のようになっていることが分かります。
A_d=e^{AT_s},
B_d=\int^{T_s}_0 e^{A\tau}d\tau B,
C_d=C
今,サンプル$k$における状態量が$x^{\rm s}[k]$であり,次サンプル$k+1$の目標状態量が$x^{\rm d}[k+1]$と表される時,サンプル$k$における入力は次のように決定すれば良いことがわかります。
x_{\rm d}[k+1]=A_{d}x^{\rm s}[k]+B_{d}u[k]\\
\therefore\ u[k]=B_{d}^{-1}(x^{\rm d}[k+1]-A_{d}x^{\rm s}[k])
マルチレート入力(リフティング)を用いた可制御性の確保
ここで,一つ問題があります。$B_{\rm d}$に逆行列が存在しない場合にはこの式は使用できません。この問題を解決するために,リフティングと呼ばれる離散時間状態空間の変換を行います。リフティングは,一定時間窓幅内の状態量を一つの状態量として再定義して,状態空間表現を再構築します。先ほどまでは1ステップ先の状態量を見ていましたが,2,3ステップ先の状態量を確認してみましょう。
\begin{align}
x[k+1]&=A_dx[k]+B_du[k]\\
x[k+2]&=A_dx[k+1]+B_du[k+1]\\
&=A_d^2x[k]+A_dB_du[k]+B_du[k+1]\\
&=A_d^2x[k]+
\begin{bmatrix} A_dB_d & B_d \end{bmatrix}
\begin{bmatrix} u[k] \\ u[k+1] \end{bmatrix}\\
x[k+3]&=A_dx[k+2]+B_du[k+1]\\
&=A_d^3x[k]+A_d^2B_du[k]+A_dB_du[k+1]+B_du[k+2]\\
&=A_d^3x[k]+
\begin{bmatrix} A_d^2B_d & A_dB_d & B_d \end{bmatrix}
\begin{bmatrix} u[k] \\ u[k+1]\\ u[k+2] \end{bmatrix}
\end{align}
このように,複数ステップ後の状態量に着目する,もしくは入力多重化(マルチレート入力)を行うことで入力行列$B_d$に当たる部分が拡張されていきます。この入力行列ですが,制御理論では有名な可制御行列です。つまり,可制御なシステムに対しては,リフティングされたシステムの入力行列の逆行列が存在します。可制御性は,離散化におけるサンプリング時間に対する依存性が非常に小さく,この手法は非常に汎用的であると言えます。
Matlabを用いた実装
Matlabを用いて,実際に制御系の構成方法を見ていきましょう。実は非常に簡単に組むことができます。次のように表現される2次の連続時間のプラントを使用します。
\begin{align}
&\ddot{x}=-30x(t)-0.2\dot{x}(t)+2u(t)\\
\Longleftrightarrow&\left\{
\begin{matrix}
\begin{bmatrix} \dot{x}(t) \\ \ddot{x}(t) \end{bmatrix}=
\begin{bmatrix} 0 & 1 \\ -30.0 & -0.2 \end{bmatrix}
\begin{bmatrix} x(t) \\ \dot{x}(t) \end{bmatrix}+
\begin{bmatrix} 0 \\ 2 \end{bmatrix}u(t)\\
y=\begin{bmatrix} 1 & 0 \end{bmatrix}
\begin{bmatrix} x(t) \\ \dot{x}(t) \end{bmatrix}
\end{matrix}
\right.
\end{align}
% System model (Continuous-time domain)
Ap = [ 0 1 ; -30.0 -0.2 ];
Bp = [ 0 ; 2 ];
Cp = [ 1 0 ];
Dp = 0;
Plant_pp=ss(Ap,Bp,Cp,Dp);
上のモデルに適用することを考えて,システム同定して下のようなモデルを得ているとします。
% System (Continuous-time domain)
FluctuationRate=[1.0 1.0];
Ac = Ap*FluctuationRate(1,1);
Bc = Bp*FluctuationRate(1,2);
Cc = Cp;
Dc = Dp;
Plant_cc=ss(Ac,Bc,Cc,Dc);
モデルの離散化は,c2dコマンドで行います。入力のサンプリングレートを10 kHzとして離散化を行います。
% Discretization
T_input=1e-4;
Plant_uz=c2d(Plant_cc,T_input,'zoh');
[As,Bs,Cs,Ds]=ssdata(Plant_uz);
ここで,リフティング後の入力行列が逆行列を持つためには,入力行列が2x2の行列である必要があります。そのため,入力多重度は2となります。
% Lifted model
Mrate = 2.0;
A = As^2;
B = [A*Bs Bs];
指令値$x^{\rm d}$が決まったら, $u[k]=B^{-1}(x^{\rm d}[k+1]-Ax^{\rm d}[k])$とするだけです。今回の場合,リフティングを行なっているので実際には$[u[k]\ u[k+1]]^{\mathrm T}=B^{-1}(x^{\rm d}[k+2]-Ax^{\rm d}[k])$です。入力は,全状態量が初期状態から滑らかに変化する必要があります。そのため,状態量の指令値を次のように生成しました。
% Command
T_finish=10.0;
T_sample=Mrate*T_input;
t_sample = 0:T_sample:T_finish;
Amp=1.0;
Freq=1.0;
Xz0=CmdGenerator(Amp,Freq,t_sample);
Xz1=CmdGenerator(Amp,Freq,t_sample+T_sample);
% Function
function y=CmdGenerator(A,f,t)
w=2.0*pi*f;
x=(A/2.0)*(1.0-cos(w*t));
v=(A/2.0)*w*sin(w*t);
y=[x;v];
end
指令値は振幅1.0,周波数1.0 Hzの波です。今回は状態量が変数とその微分値で構成されているため,指令値が$C^1$級に属し,かつ指令値の初期状態が状態量の初期状態と一致することが重要です。状態量の初期値と指令値の初期値が一致しない場合にはモデル化誤差が生じた際のような振る舞いを見せます。
入力の生成は次の2行で済みます。
u=B\(Xz1-A*Xz0);
u=u(:);
「u=u(:)」多重化された入力を展開するためのものです。この入力をシステムに入れてみます。
% Simulation
t_input=0:T_input:(T_finish+T_input);
x0=[0;0];
xres=lsim(Plant_pp,u,t_input,x0,'zoh');
モデル変動が0(FluctuationRate=[1 1])の際の応答は,指令値に追従しています。誤差がサンプル点において0にならないのは,計算過程の丸め込み等が原因かと思われます。フィードバック補正なしでこれだけ追従しているので,頑張っていると思います。
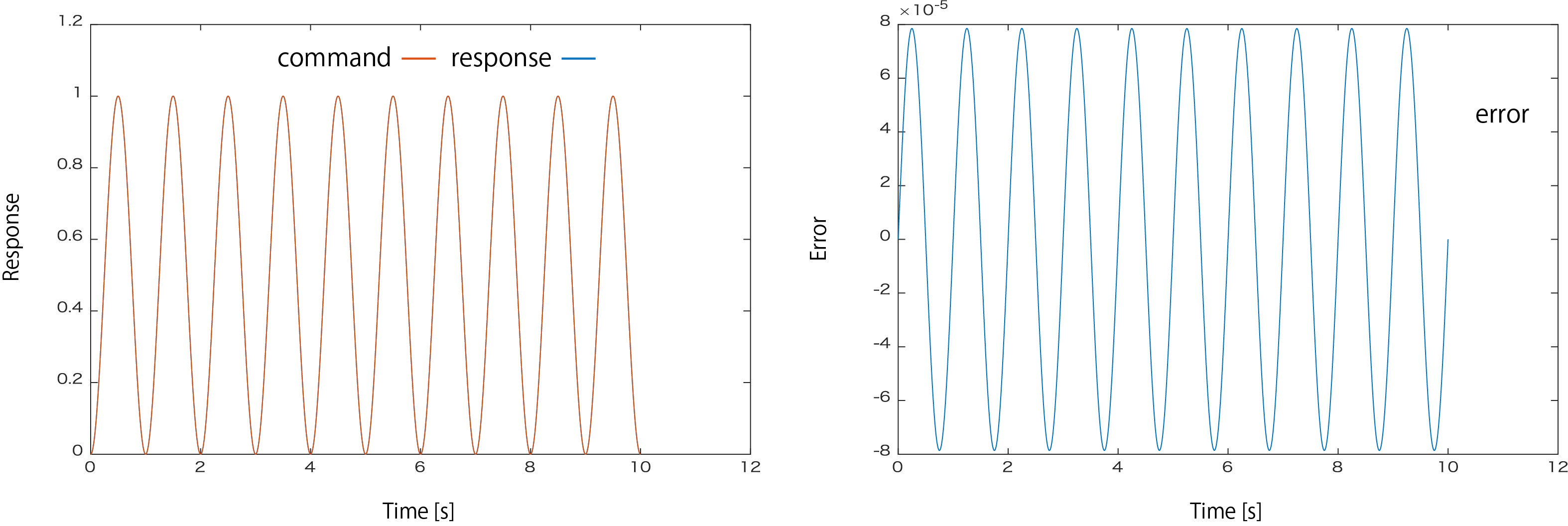
ここで,システム行列に変動やモデル化誤差があった場合(FluctuationRate=[1.2 1])の場合は次のようになります。フィードフォワードだけでは誤差が出るのは仕方ありません。
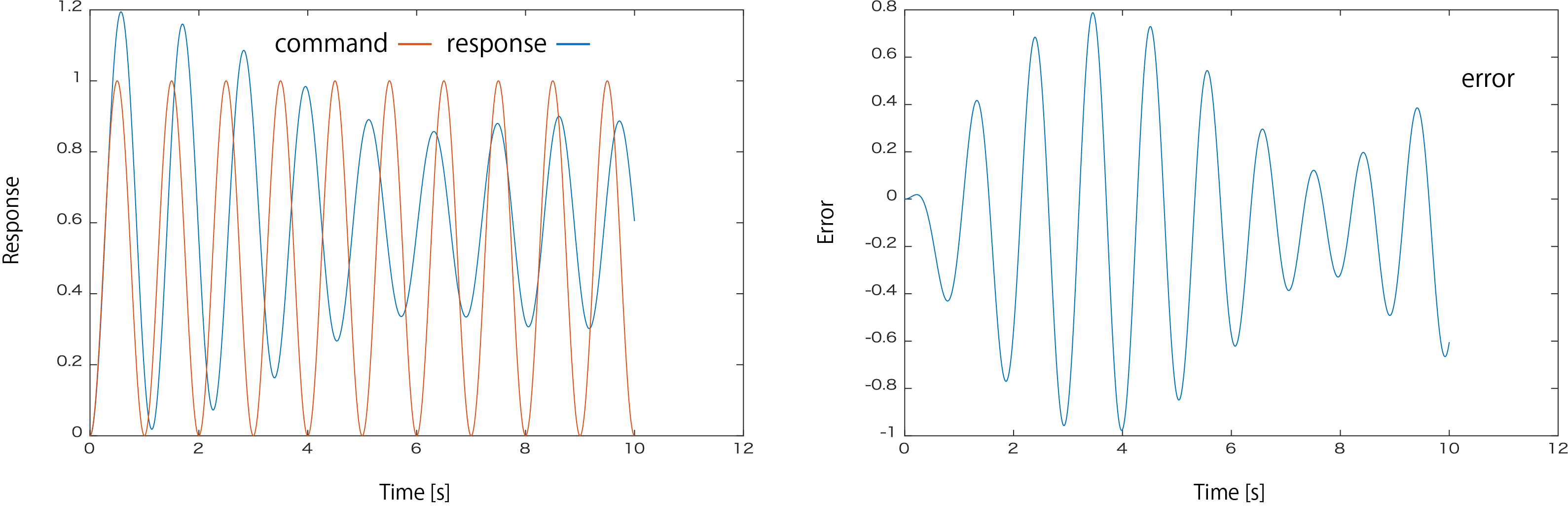
そこで,フィードバック制御器を設計して,シミュレーションを回してみます。
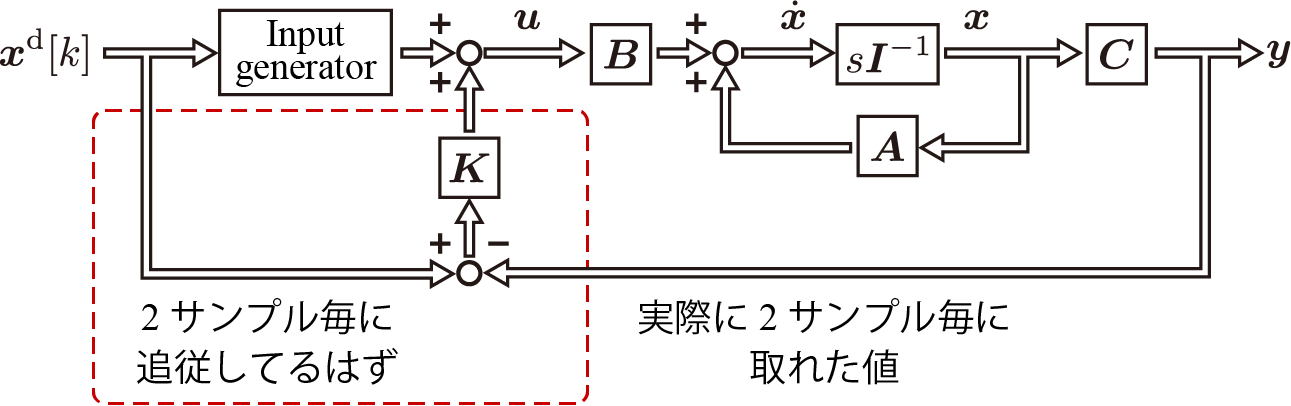
このブロック線図は,上で紹介した2自由度制御系の入力整形器$K=N^{-1}$としたものと大体等価です。上図の$K$はフィードバックゲインです。この2自由度制御系をMatlabで書くためには,次のようにシステムを書き換えて実装する必要があります。
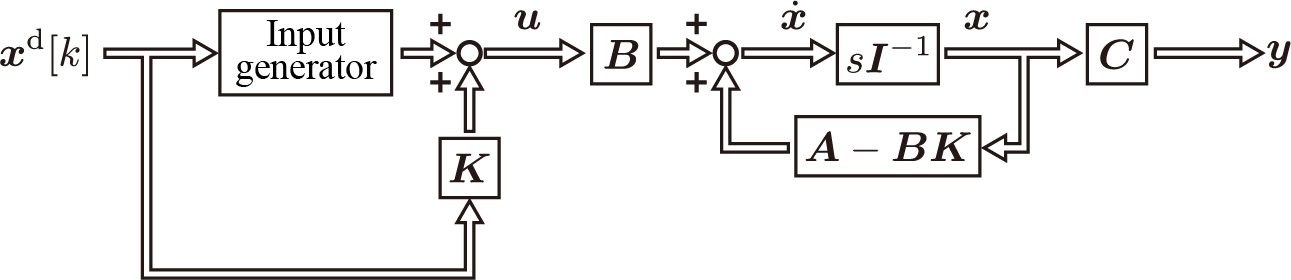
したがって,入力とシステムの両方を書き換える必要があるため,注意が必要です。下にコードを記載します(マルチレートの設定がMatlabだとよく分からなかったのでシングルレートになっています)。
% Feedback controller
Xcmd=CmdGenerator(Amp,Freq,t_input);
K=[10000 200];
u=u+(K*Xcmd)';
Plant_fb=ss(Ap-Bp*K,Bp,Cp,Dp);
% Simulation
x0=[0;0];
xres=lsim(Plant_fb,u,t_input,x0,'zoh');
誤差がしっかりと補正されました。今回は適当にPDコントローラを設計したので,ステップ外乱に対しては定常偏差が残ったりすると思いますが,2自由度制御系なので自由にフィードバック制御器を組めます。
お気付きの方もいらっしゃるかと思いますが,制御対象は減衰率の低い振動するプラントです。完全追従制御はプラントの特性を考慮した上で制御入力をするので,振動を抑えつつサンプル点追従を実現したりします。大型ステージでの実装例も報告されています。
最後に,全体のコードを載せておきます。
コード
clear;
% System model (Continuous-time domain)
Ap = [ 0 1 ; -30.0 -0.2 ];
Bp = [ 0 ; 2 ];
Cp = [ 1 0 ];
Dp = 0;
% System (Continuous-time domain)
FluctuationRate=[1.2 1.0];
Ac = Ap*FluctuationRate(1,1);
Bc = Bp*FluctuationRate(1,2);
Cc = Cp;
Dc = Dp;
%Multirate
Mrate=2.0;
% Simulation time (input system)
T_finish=10.0;
% Sampling time (input system)
T_input=1e-4;
t_input=0:T_input:(T_finish+T_input);
T_sample=Mrate*T_input;
t_sample = 0:T_sample:T_finish;
% Discretization
Plant_pp=ss(Ap,Bp,Cp,Dp);
Plant_cc=ss(Ac,Bc,Cc,Dc);
Plant_uz=c2d(Plant_cc,T_input,'zoh');
[As,Bs,Cs,Ds]=ssdata(Plant_uz);
% Lifted model
A = As^2;
B = [A*Bs Bs];
% Command
Amp=1.0;
Freq=1.0;
Xcmd=CmdGenerator(Amp,Freq,t_input);
Xz0=CmdGenerator(Amp,Freq,t_sample);
Xz1=CmdGenerator(Amp,Freq,t_sample+T_sample);
% Feedforward Controller
u=B\(Xz1-A*Xz0);
u=u(:);
% Feedback controller
fb=1;
K=[10000 200]*fb;
u=u+(K*Xcmd)';
Plant_fb=ss(Ap-Bp*K,Bp,Cp,Dp);
% Simulation
x0=[0;0];
xres=lsim(Plant_fb,u,t_input,x0,'zoh');
% Check
xcmd=Cc*CmdGenerator(Amp,Freq,t_input);
error=xcmd-xres';
figure(1);
plot(t_input,xres); hold on;
plot(t_input,xcmd); hold on;
figure(2);
plot(t_input,error); hold on;
% Function
function y=CmdGenerator(A,f,t)
w=2.0*pi*f;
x=(A/2.0)*(1.0-cos(w*t));
v=(A/2.0)*w*sin(w*t);
y=[x;v];
end
おわりに
産業ではフィードフォワード技術が多く使われており,モデル化技術が非常に大きな役割を果たしています。名古屋工業大学や東京大学の研究グループはモデル化とフィードフォワード技術に非常に長けており,面白い研究が多いですね。
上記の完全追従制御ですが,入力がサンプル区間内一定という仮定は,モータ制御などでは電流制御系の遅れなどから厳しい場合があります。これに対し,電圧インバータのPWM制御において厳密モデル化を行って完全追従制御を行なっていたりします。高速かつ精密な位置決めを実現していて凄いですね。
参考文献:
Dead beat microprocessor control of PWM inverter for sinusoidal output waveform synthesis, K. P. Gokhale, A. Kawamura, and R. G. Hoft, IEEE Trans. on Ind. App., Volume: IA-23, Issue 5, pp. 901-910, 1987.
Hiroshi Fujimoto and Koichi Sakata, Multirate PWM Control of Precision Stage for Ultrahigh-Speed Nanoscale Positioning, IEEJ Journal of Ind. App., vol. 3, no. 3, pp. 270-276, 2014.
12/30追記
@motorcontrolman様よりコメント欄にてコードの誤りをご指摘いただきました。
修正前
A = As^2;
B = [A*Bs Bs];
修正後
A = As^2;
B = [As*Bs Bs];
変数名を間違えて,ブロッキング後表現の入力行列Bの生成に同ブロッキング表現のシステム行列Aを使用していました。完全に誤りなのですが,何故かフィードフォワード入出力応答確認のシミュレーションがそれとなく動作してしまい,気がつきませんでした(おそらく,サンプリング周波数が高かったため,システム行列$A_s$による1ステップの状態遷移と2ステップの状態遷移(=ブロッキング表現におけるシステム行列$A$による1ステップ)の状態遷移の量が近く,モデル誤差が小さかった)。コードを修正した後に行なったフィードフォワード入出力応答確認のシミュレーション結果は次のようになりました。
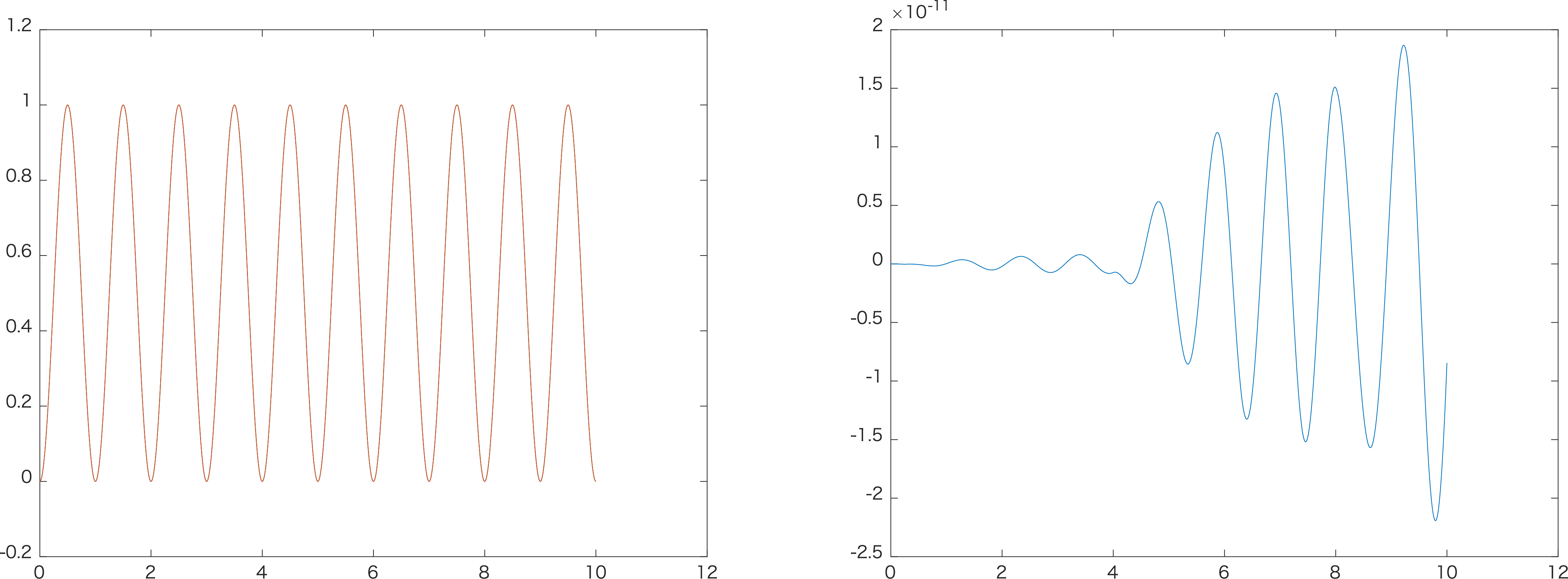
誤りのあるコードによるシミュレーション結果から,誤差が大きく低減されました。
制御工学 Advent Calendar 2019 23日目に@fumiya_sato様より,本記事と同じくフィードフォワード制御である終端状態制御に関する記事が掲載されています。
式導出は非常に似ておりますが,指令値決定の自由度に差異があります。完全追従制御は予め決められた連続時間空間の軌道情報を基に,制御入力を決定します。このとき,フィードフォワード入力の決定周期は,入力サンプラとシステムの次数を乗算した周期(コード上ではMrateT_input)となります。終端状態制御は動作する時間(到達時間),開始と終了時の状態量を与え,制御開始前に一連のフィードフォワード入力を決定します。このとき,到達時間までに状態量を初期状態から終了状態まで遷移させるためのフィードフォワード入力は無限に存在し(冗長な系),この冗長性によって制御系に機能を持たせることができます(完全追従制御は冗長性を排して(MrateT_input)周期でのサンプル点追従を行なっています)。終端状態制御は,完全追従制御が連続時間空間において軌道を設計する都合上,サンプル点間応答を積極的に考慮することができないことを指摘し,サンプル値制御系(簡素にはサンプル点間応答まで含めて離散制御系設計を行う,という枠組み)を念頭に,冗長性を活用してフィードフォワード入力の最適化整形を行なっています。取り扱う系にもよりますが,振動する系に対して完全追従制御を適用してサンプル点間応答を見てみると,振動していたりします。この振動の程度によっては,サンプル値制御系に基づき,終端状態制御の拡張系である周波数整形型終端状態制御の適用を考慮すると良いのかもしれません。どちらが良いかについては,用途次第で,フォトリゾグラファのようなある時間に特定の場所にを通過していなければならない等の軌道経路の制約がある場合に,完全追従制御は非常に有効と考えられます。
参考文献:
平田 光男, 長谷川 辰紀, 野波 健蔵, 終端状態制御によるハードディスクのショートシーク制御, 電気学会論文誌D(産業応用部門誌), 125 巻, 5 号, p. 524-529, 2005.
平田 光男, 城所 隆弘, 長距離移動のための終端状態制御, 計測自動制御学会論文集, 45 巻, 12 号, p. 696-702, 2009.