まえがき
Advent Calendar 2019[制御工学]の記事になります。
年々皆様の記事が手の込んだものになってきており、
そろそろついていけなくなりそうな今日この頃です。
今回は、フィードフォワード制御の一種である終端状態制御の
基礎を追ってみます。最後に、重み(評価関数?)となるQの与え方による
制御結果への影響をシミュレーションしてみます。
参考文献[1]を引用する形で進め、適宜補足を入れる形としました。
また、執筆時間の関係上、シミュレーションのみで実機適用がないことはご了承ください。
理論
背景
終端状態制御は,あるシステムに対し,フィードフォワード入力を与えることで
有限時間で指定した終端状態にもってゆく制御法である。
無理やり言い換えると、「初期状態と希望する終端状態が与えられたときにそれを実現する
フィードフォワード入力をいい感じに求めましょう」になります。
問題設定
今回の制御対象のシステムは次式であらわされる、可制御な1入力のm次離散時間システムです。
$\boldsymbol{x}[t+1]=A\boldsymbol{x}[t]+Bu[t]\tag{1}$
このシステムに対して、初期状態$\boldsymbol{x}[0]$が分かっており、
終端状態$\boldsymbol{x}[N]$となるように制御したいと思います。
それを実現する$\boldsymbol{U}
=[u[0],u[1], \dots ,u[N-1]]^T \tag{2}$
を求めることが今回の問題になります。
注意点として**$N\ge m$**でないとなりません。
離散時間で考えると、直感的にはある単一の入力がm次の状態に影響を
与えるには、mステップないとですよね?
導出
では問題となってくるのが、一般に$\boldsymbol{U}$は一意に定まらないことだそうです
(証明は探していないため一意に定まる場合がどんなか不明)。
そこで次の用に評価関数$J$を設定し、これを最小とする$\boldsymbol{U}$を制御入力とします。
$J=\boldsymbol{U}^T\boldsymbol{Q}\boldsymbol{U},\boldsymbol{Q}>0 \tag{3}$
※$\boldsymbol{Q}$は正定な対称行列となるよう与えます。
この$\boldsymbol{Q}$を如何に設定するかが制御結果に影響を与えることになります。
さて、Jを最小化するためにラグランジュの未定乗数法を適用することを考えます。
解説:Wiki
Jを最小化するうえでの束縛条件は、式(1)のシステムの下で、初期状態$\boldsymbol{x}[0]$のときに、
終端状態を$\boldsymbol{x}[N]$とすることです。このままではラグランジュの未定乗数法の束縛条件として
利用できないので、式(1)を展開することで数式で表現します。
式(1)を展開すると、
\begin{align}
\boldsymbol{x}[N] &= A\boldsymbol{x}[N-1]+B\boldsymbol{u}[N-1]\\
&=B\boldsymbol{u}[N-1] + A(A\boldsymbol{x}[N-2]+B\boldsymbol{u}[N-2])\\
&=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2\boldsymbol{x}[N-2]\\
&=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2(A\boldsymbol{x}[N-3]+B\boldsymbol{u}[N-3])\\
&=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2B\boldsymbol{u}[N-3]+A^3\boldsymbol{x}[N-3]\\
&=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2B\boldsymbol{u}[N-3]+\dots
+A^{i-1}B\boldsymbol{u}[N-i]+\dots+A^{N-1}B\boldsymbol{u}[0]+A^N\boldsymbol{x}[0]\\
\end{align}
右辺の$\boldsymbol{x}[0]$の項だけ左辺に移項して、
\begin{align}
\boldsymbol{x}[N] - A^N\boldsymbol{x}[0] &=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2B\boldsymbol{u}[N-3]+\dots
+A^{i-1}B\boldsymbol{u}[N-i]+\dots+A^{N-1}B\boldsymbol{u}[0]\\
&=B\boldsymbol{u}[N-1] + AB\boldsymbol{u}[N-2]+A^2B\boldsymbol{u}[N-3]+\dots
+A^{i-1}B\boldsymbol{u}[N-i]+\dots+A^{N-1}B\boldsymbol{u}[0]\\
&=[A^{N-1}B,\dots,A^{N-i},\dots,AB,B]\times
\begin{bmatrix}
\boldsymbol{u}[0] \\ \boldsymbol{u}[1] \\ \vdots \\
\boldsymbol{u}[N-i] \\ \vdots \\ \boldsymbol{u}[N-1]
\end{bmatrix}
\end{align}
ここで、$\boldsymbol{\Sigma}$を以下の式(4)とします。
$\boldsymbol{\Sigma}=[A^{N-1}B,\dots,A^{N-i},\dots,AB,B] \tag{4}$
よって、式(3)に式(4)を代入することで、
\begin{align}
\boldsymbol{x}[N] - A^N\boldsymbol{x}[0] =\boldsymbol{\Sigma} \boldsymbol{U}
\end{align}
移項して、
\begin{align}
\boldsymbol{x}[N] - A^N\boldsymbol{x}[0] -\boldsymbol{\Sigma} \boldsymbol{U}=0
\end{align}
定数項を**$X=\boldsymbol{x}[N] - A^N\boldsymbol{x}[0]$**とすると、
$X -\boldsymbol{\Sigma} \boldsymbol{U}=0\tag{5}$
やっと、式(5)を束縛条件として式(3)を最小化するUをラグランジュの未定乗数法で求め始められます。
まず、未定乗数ベクトルを$2\lambda$とすることで次式が成り立つ。
$J=\boldsymbol{U}^T\boldsymbol{Q}\boldsymbol{U} + 2\lambda(X -\boldsymbol{\Sigma} \boldsymbol{U}) \tag{6}$
式(6)について、$\boldsymbol{Q}$が正定なのでJの最小値は常に存在し、(証明未確認)
次式を満たします。
\begin{align}
\frac{\partial J}{\partial U}&=0\\
\therefore 2\boldsymbol{Q}\boldsymbol{U}-2\boldsymbol{\Sigma}^T \lambda^T&=0\\
\end{align}
さて、$\boldsymbol{Q}$が正定なので逆行列を持つ。よって移項して整理すると、
$\boldsymbol{U}=\boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T \lambda^T \tag{7}$
一方で、式(5)と式(7)より、
\begin{align}
X -\boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T \lambda^T=0\\
\therefore \boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T \lambda^T = X\tag{8}
\end{align}
式(1)のシステムは可制御なので、$\Sigma$は行フルランクなため、
\begin{align}
|\boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T| \neq0
\end{align}
である。よって式(8)から、
$\lambda^T = (\boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T )^{-1}X\tag{9}$
式(9)を式(7)に代入することで最終的に
\begin{align}
\boldsymbol{U}&=\boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T (\boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T )^{-1}X\\
\therefore \boldsymbol{U}&=\boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T (\boldsymbol{\Sigma} \boldsymbol{Q}^{-1}\boldsymbol{\Sigma}^T )^{-1}(\boldsymbol{x}[N] - A^N\boldsymbol{x}[0]) \tag{10}
\end{align}
以上、式(10)によって、初期状態と終端状態およびQを与えれば、フィードフォワード入力$\boldsymbol{U}$を計算できる。
シミュレーション
対象のシステム
シミュレーション対象とする仮想システムは式(1)のA,B,C,Dとして以下を設定しました。
なお、観測方程式は今回不要のため、記載していません。
(以前の記事で求めたDCモータのモデルです)
\boldsymbol{x}[t+1]=
A
\begin{bmatrix}
0 & 1\\
0 & -117.1\\
\end{bmatrix} \boldsymbol{x}[t]
+B
\begin{bmatrix}
0 \\ 99.16
\end{bmatrix}\boldsymbol{u}[t]
Qの与え方による違い
さて、では本題として$\boldsymbol{Q}$の与え方による結果の違いを見ていきます。
$\boldsymbol{Q}$は以下の3種類についてシミュレーションを実施しました。
対角成分以外は0としました。
Q1=\begin{bmatrix}
1 &0 &\dots & 0 \\
0 & 1 & \dots &0 \\
\vdots &\vdots &\ddots & \vdots \\
0 &0 &0 &1
\end{bmatrix},
Q2=\begin{bmatrix}
1 &0 &\dots & 0 \\
0 & 2 & \dots &0 \\
\vdots &\vdots &\ddots & \vdots \\
0 &0 &0 &N
\end{bmatrix},
Q3=\begin{bmatrix}
1 &0 &\dots & 0 \\
0 & 2 & \dots &0 \\
\vdots &\vdots &\ddots & \vdots \\
0 &0 &0 &N^2
\end{bmatrix}
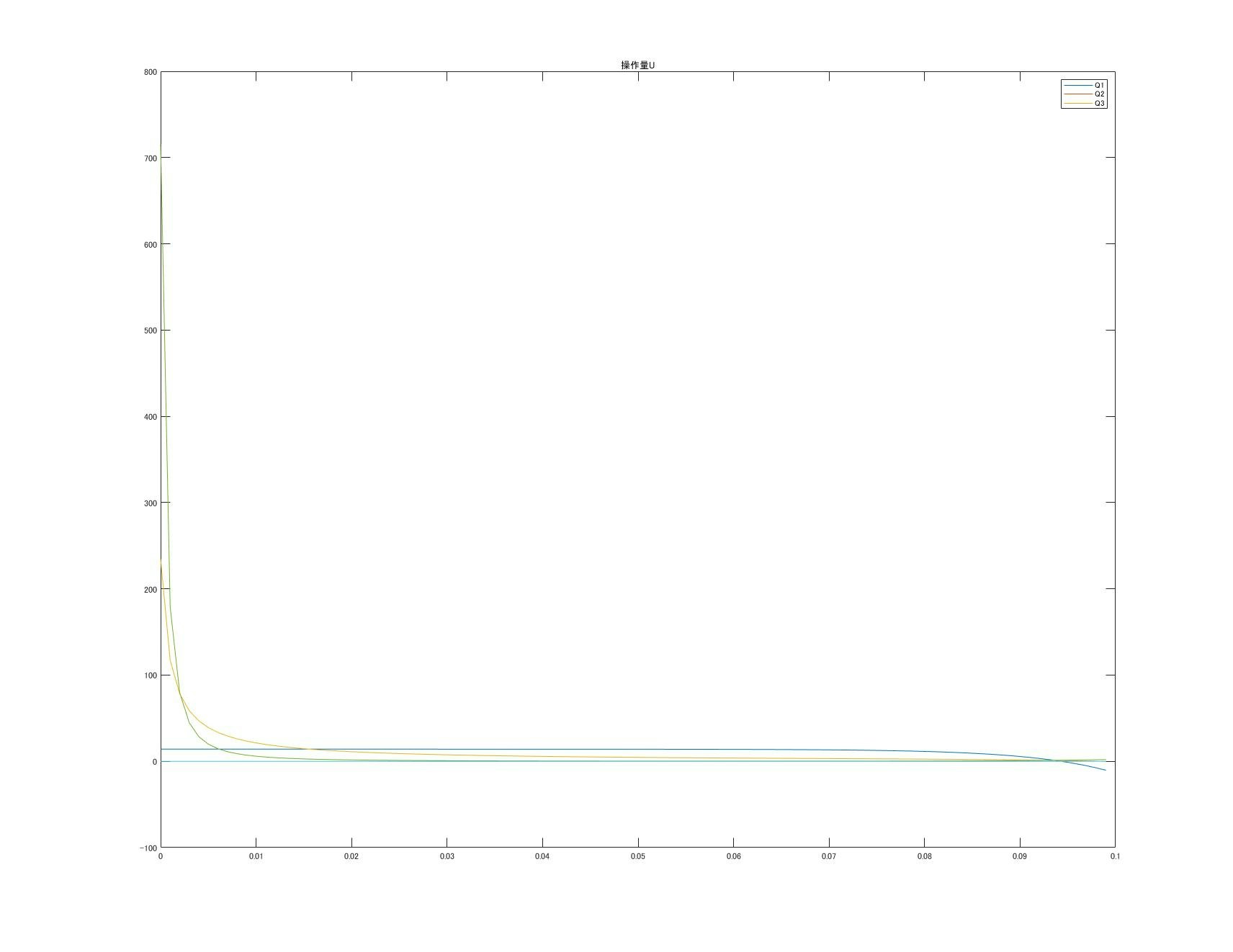
いきなり結果に行きます。
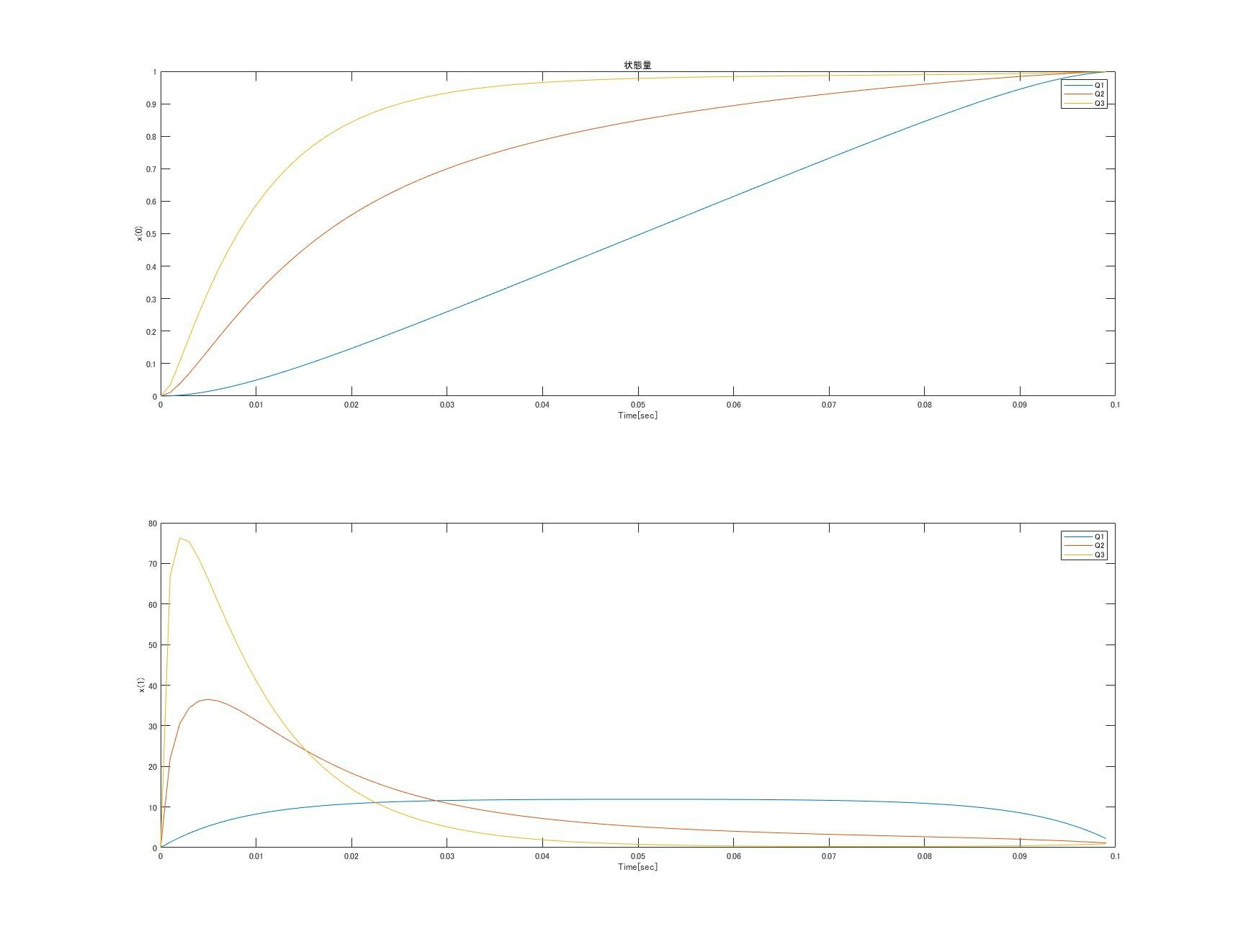
図1 状態量のシミュレーション結果
ということで重みに応じて操作量の算出結果が変化しております。
誤差が残ってしまっていますが、シミュレーションを離散系で行ったことに起因する誤差だと
考えられます。Nを充分に大きくしたら重みによらず終端状態に収束しました。
コメントでご指摘いただけましたように、シミュレーションを間違っていました。
しっかりと終端状態にいたっています。
参考文献ではこの終端状態制御をベースに周波数をうまく評価部分に組み込むことで、
HDDの応答性能について議論しておりますので、興味が出てきた方はそちらをどうぞ。
あとがき
Advent Calenderに間に合わせるために特急仕事となってしまいました。
各所しっかりと証明の確認や、式展開をしてみたかったのですが、結局全然できませんでした・・・
(気が向いたら追記したいです)。
誤りがありましたら積極的にコメントお願いします。
参考文献
[1]山口高司・平田光男・藤本博志 ナノスケールサーボ制御 高速・高精度に位置を決める技術
参考MATLABコード
clear all;
close all;
A=[0 1;
0 -117.1];
B=[0;99.16];
C=[1 0;0 1];
D=[0;0];
Ts=1e-3;
sys_c=ss(A,B,C,D)
system_d= c2d(sys_c,Ts);
N=100; %終端状態を何ステップ先にするか?
t=0:Ts:(N-1)*Ts;
x_init=[0;0]; %初期状態
x_last=[1,0]; %終端状態
% シグマの算出
Sigma =zeros(0);
for i=0:N-1
Sigma=horzcat(system_d.A^i*system_d.B、Sigma);
end
% Qの設定
Q1=diag(ones(N,1));
Q2=diag([1:1:N]);
Q3=diag([1:1:N]).^2;
% Q3=diag([N:-1:1]); %N→1に重みを下げた場合
% 出力x
U1=Q1\ transpose(Sigma) * inv((Sigma * inv(Q1) * transpose(Sigma))) * (x_last - x_init);
[y1,t,x1]=lsim(system_d,U1(:,1),t,x_init);
U2=Q2 \ transpose(Sigma) * inv((Sigma * inv(Q2) * transpose(Sigma))) * (x_last - x_init);
[y2,t,x2]=lsim(system_d,U2(:,1),t,x_init);
U3=Q3 \ transpose(Sigma) * inv((Sigma * inv(Q3) * transpose(Sigma))) * (x_last - x_init);
[y3,t,x3]=lsim(system_d,U3(:,1),t,x_init);
subplot(2,1,1);
plot(t,x1(:,1),t,x2(:,1),t,x3(:,1));
xlabel('Time[sec]');ylabel('x(0)');
legend('Q1','Q2','Q3');title('状態量');
subplot(2,1,2);
plot(t,x1(:,2),t,x2(:,2),t,x3(:,2));
xlabel('Time[sec]');ylabel('x(1)');
legend('Q1','Q2','Q3');
% 操作量u
figure();
plot(t,U1,t,U2,t,U3);title('操作量U');
legend('Q1','Q2','Q3');
% 一部拡大(状態x)
figure();
subplot(2,1,1);
plot(t,x1(:,1),t,x2(:,1),t,x3(:,1));
xlabel('Time[sec]');ylabel('x(0)');
xlim([N*0.9*Ts N*Ts]);
legend('Q1','Q2','Q3');title('状態量(x軸一部抜粋)');
subplot(2,1,2);
plot(t,x1(:,2),t,x2(:,2),t,x3(:,2));
xlabel('Time[sec]');ylabel('x(1)');
xlim([N*0.9*Ts N*Ts]);
legend('Q1','Q2','Q3');title('状態量(x軸一部抜粋)');
% 一部拡大(操作量u)
figure();
plot(t,U1,t,U2,t,U3);title('操作量U(y軸拡大)');
ylim([0 10]);
legend('Q1','Q2','Q3');