はじめに
(2019/10/01)@erosionさんに指摘して頂いた箇所を追加しました
MLPの「ガウス過程と機械学習」の方を読むことをおすすめします。
1週間前にDeepMindからBayesian Optimization in AlphaGo が発表されたばかりです.
本論文ではベイズ最適化を用いてAlphaGoのハイパーパラメータを決定しています.
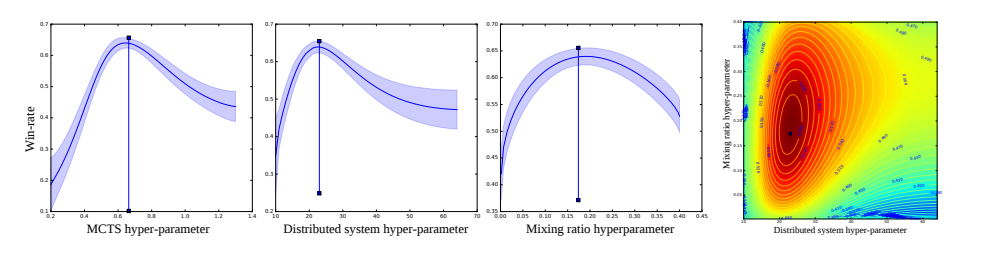
囲碁のように強い非線形性を持つ関数(今回はDNN)において,局所最適解に陥らないように大域的最適解を得ることは非常に難しいです.
そこで,ベイズ最適化は非線形関数の最大値(もしくは最小値)を探索するのに役立ちます.
研究で使おうと思ったのでここでまとめたいと思います.
2日間で勉強した内容なので間違っていたら教えてください.
おしながき
- ベイズ最適化とは & 全体のアルゴリズム
- ガウス過程回帰の更新式
- ベイズ
- 条件付きガウス分布
- ガウス過程
- 線形回帰
- ガウス過程による回帰
- カーネル関数
- カーネル関数を導入する理由
- 獲得関数の更新式
まとめと感想
の順に説明していきます.
ベイズ最適化とは
関数$y=f(x)$の最小値(最大値)を逐次的に+確率的に探索する手法です.
下記は最小値のものを導出します。
例えば,AlphaGoであれば勝率を最小にしそうなパラメータを探索し,最小値を見つけます.
***「しそうな」***というのは確率的にそこが大きくなるだろうとベイズ的に予測しているからです.
ここで学習器は当然$f(x)$がどういう形をしているか分かりません.関数に$x$投げたら$y$が返ってくるだけとします.
大まかにアルゴリズムの説明します
とりあえず初期値としてn点とる
while(n==max回数)
1. ガウス過程で平均・分散を計算(推定)
2. (目的関数の代わりの)Acquisition Functionを更新・次の探索点を選択
3. 最小となる点をサンプル
4. n += 1
最小化してみましょう
とりあえずn点
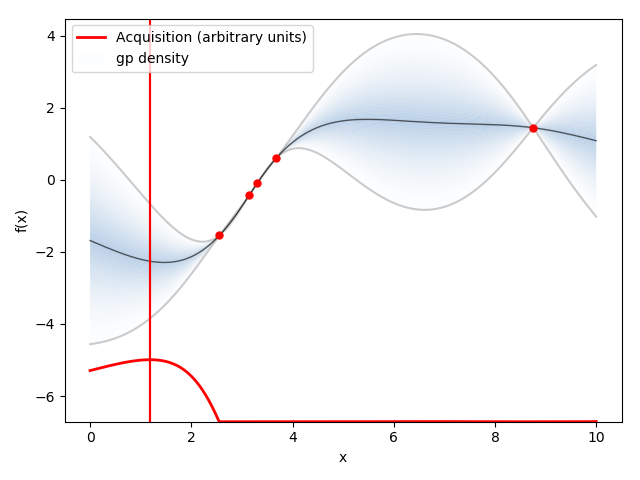
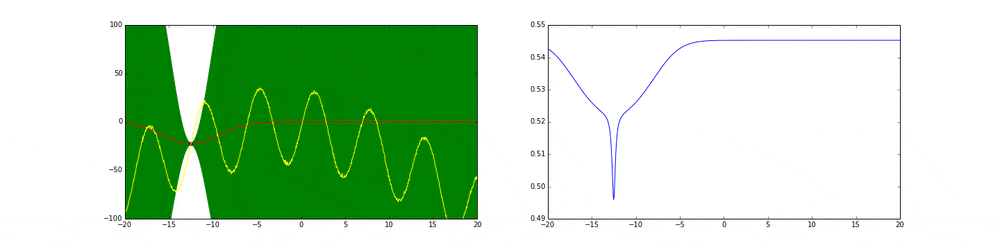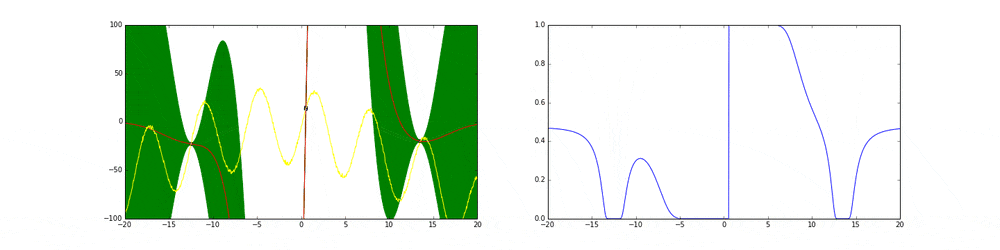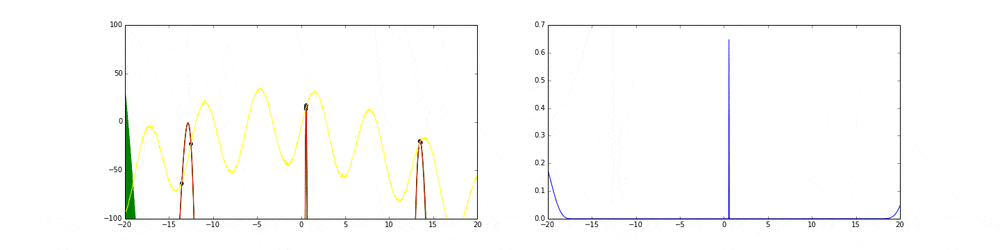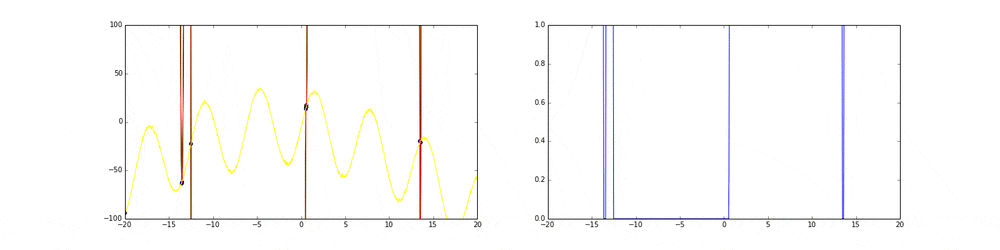
元の関数として青の線のような関数$y=f(x)$があったとします.
まずはアルゴリズム通りn点サンプリングしてきましょう.
紫の点がサンプリングです.
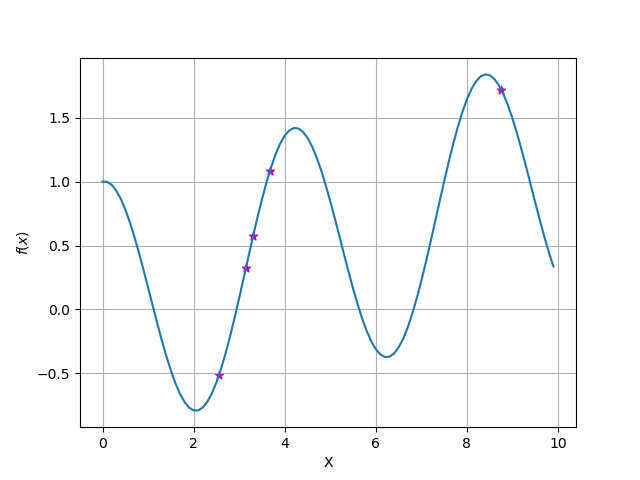
1. ガウス過程回帰で平均・分散を計算(推定)
推定された関数(の平均)を黒線で表します.
薄い青で囲われたところは分散を表します.
ガウス過程は後ほど説明しますが,横軸が$x$だとすると,各サンプリングした$x_i$に対してガウス分布を保持・計算します.この図だとn=5 (i=1,2・・・,n)です.
更新式
\begin{align}
m({\bf x}_{N+1}) & = {\bf k}^{\rm T}{\bf K}_N^{-1}{\bf y}_{1:t}, \\
\sigma^2({\bf x}_{N+1}) & = k – {\bf k}^{\rm T}{\bf K}_N^{-1}{\bf k}
\end{align}
$\bf k$はカーネルを表しています.後ほど説明します
\begin{align}
k({\bf x}, {\bf x}^{\prime}) & = \theta_0 \exp \Bigl( -\frac{\theta_1}{2} | {\bf x} – {\bf x}^{\prime} |^2 \Bigr) + \theta_2 + \theta_3\bf x^T {\bf x}^{\prime} \\
K_{n,m} & = k(\bf x_n, \bf x_m)
\end{align}
2. Acquisition Functionを更新・次の探索点を選択
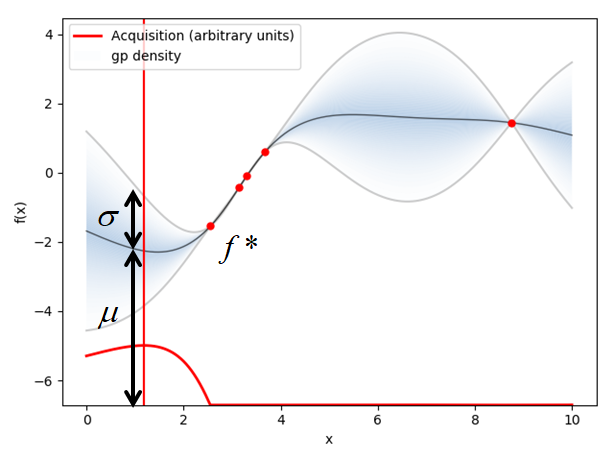
ここで,Acquisition Functionは様々ありますが,基本として平均$\mu$と分散$\sigma$を足したもの ($\mu + \kappa\sigma$はExpected Improvementではなく、Upper Confidence Boundでした)で探索(exploration)と搾取(exploitation:利用)の"指標"である目的関数Acquisition Function(獲得関数)を定義します.
$\mu$は今までの情報の搾取を,$\sigma$は探索を意味し,$\kappa$はどちらをより多く重視するかを表すハイパーパラメータです.ちなみに搾取を強調したい場合$\kappa=0.01$ぐらいに設定します.
下に示している赤い線が獲得関数です.
獲得関数が最大となる箇所が次サンプリングすべき点$x$です.
更新式
Upper Confidence Bound
UCB(\mathbf{x}) = \mu(\mathbf{x}) + \kappa\sigma(\mathbf{x})
Expected Improvement
EI(\mathbf{x}) = (f^* - \mu(\mathbf{x}))\Phi(\frac{f^*-\mu(\mathbf{x})}{\sigma(\mathbf{x})}) + \sigma(\mathbf{x}) \phi(\frac{f^*-\mu(\mathbf{x})}{\sigma(\mathbf{x})})
3. 最小となる点をサンプルし,再度1に戻る.
次にサンプリングすべき点
\mathbf{x}^* = argmax (EI(\mathbf{x}))
1に戻ります!
ここから導出していきます!
数学
まず,①の「サンプリング点からその他全ての点の平均と分散を計算」する手法を導出します(ガウス過程回帰の更新式)
次に,②の「最大にしそうな点を表す目的関数である,獲得関数を計算」する手法を導出します(獲得関数の更新式)
ガウス過程の更新式の導出
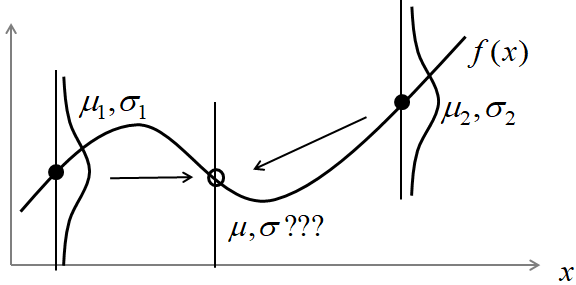
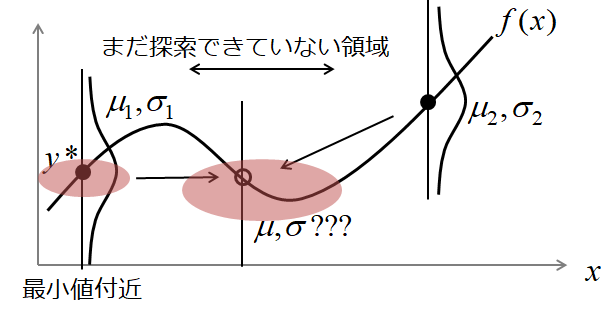
ガウス過程の目的は,図のようにサンプリング点$x_1, ..., x_N$における観測値$y_1, ..., y_N$から,その他の領域における点$x$での$y(x)$の平均と分散を求めることです.
さらにベイズ最適化では,ガウス過程による回帰に,ベイズ的考えである「条件付きガウス分布」を用いて逐次更新していきます. (ベイズ最適化におけるベイズとはベイズ的な回帰手法であるガウス過程回帰(ないしはベイズ線形回帰)をもちいていることが由来です。との指摘を頂きました。)
人間であれば,適当にサンプリングした観測値$y_1, ... , y_3$から,一番小さかった$y*$の周りや,まだ探索していない領域を重点的にサンプリングします.
値が小さかった=平均が小さい
まだ探索していない=分散が大きい
というように周りの点の平均と分散を予測します.
このように,過去にサンプリングした値から予測された分布を「条件付き確率分布」といい,
2つの変数集合(過去のサンプリング&次の点)がガウス分布に従うとき,**「条件付きガウス分布」**と呼びます.
条件付きガウス分布
上記の図で,得られた観測値を独立な正規分布として見なすのはなく,同一の$\mathbf{y}$から発生した互いに素なデータであると考えます.
つまり,各点$\mathbf{x}_i$におけるガウス分布$y_i \sim \mathcal{N}(\mu_i,\sigma_i)$(縦に分布)はそれぞれ横方向に関係していると考えます.
ここで関係とは,同一の確率分布$\mathbf{y}$から発生しているということを表しています.
$$\mathbf{y} \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{\Sigma})$$
$\mathbf{y}$から発生した互いに素な部分集合$\mathbf{y}_a$, $\mathbf{y}_b$に分割しても,その分布の一般性は失われません.
{
\begin{bmatrix}
\mathbf{y}_a \\ \mathbf{y}_b
\end{bmatrix}
\sim \mathcal{N}
\begin{pmatrix}
\begin{bmatrix}
\boldsymbol{\mu}_a \\ \boldsymbol{\mu}_b
\end{bmatrix},
\begin{bmatrix}
\mathbf{\Sigma}_{aa} & \mathbf{\Sigma}_{ab} \\ \mathbf{\Sigma}_{ba} & \mathbf{\Sigma}_{bb}
\end{bmatrix}
\end{pmatrix}
}
$\mathbf{y}_a, \mathbf{y}_b$は,同一の分布から派生しているので,当然独立ではなく関係を持ちます。
例えば,10回正規分布に従う乱数を発生させ,全て正だった場合,次に負が出る確率は高くなります。
このように,"条件"によって確率分布が変化することを条件付き分布といい、
$\mathbf{y}_a$と$\mathbf{y}_b$の関係を条件付き分布で表すと,
\mathbf{y}_a | \mathbf{y}_b \sim \mathcal{N}(\boldsymbol{\mu}_{a|b}, \mathbf{\Sigma}_{a|b})
となり,それぞれ平均と分散の更新は以下のようになります.
\begin{align}
\boldsymbol{\mu}_{a|b} & = \boldsymbol{\mu}_{a} + \mathbf{\Sigma}_{ab} \mathbf{\Sigma}_{ab}^{-1}(\mathbf{x}_{b} – \boldsymbol{\mu}_{b}),\\
\mathbf{\Sigma}_{a|b} & = \mathbf{\Sigma}_{aa} – \mathbf{\Sigma}_{ab} \mathbf{\Sigma}_{bb}^{-1} \mathbf{\Sigma}_{ba} \\
\end{align}
導出はPRML2.3.1に記載されています.
以上の部分がベイズ最適化における「ベイズ」の部分にあたります.
今まではある2つのガウス分布を考えてきました.1つが分かればもう一つのガウス分布の形が求まります.
これは離散のものにでも利用可能です.
次はこの条件付きガウス分布を用いて,ある関数への回帰を行います.
ガウス過程
先程は,2つの部分集合の同時確率から条件付きガウス分布を導きました.
回帰でも同様に,観測値ベクトル$\bf y$の同時分布$p({\bf y}) = p(y_1, ... , y_n, y_{n+1})$を導出した後,
上記の式を用いて条件付きガウス分布$p(x_{n+1}|{\bf x}_{1:n})$を導きます.
線形回帰
以下のような線形結合で表された関数があるとします.
ここで,$\bf \phi(x)$を基底関数ベクトル(非線形関数でもOK),$\bf w$を重みベクトルとします.
f(\bf x) = \bf w^T \bf \phi(\bf x)
ここで重みベクトルの事前分布として,等方的なガウス分布,すなわち次の分布を考えます.
p(\bf w) = \mathcal{N}({\bf w} | {\bf 0}, \alpha^{-1} {\bf I})
ここで$\alpha$はハイパーパラメータであり,分布の精度を表します(分散の逆数).
$\bf f$の平均と分散は
\mathbb{E} [{\bf f}] = {\bf 0} \\
cov[{\bf f}] = {\bf K} \\
K_{nm} = k({\bf x_n}, {\bf x_m}) = \frac{1}{\alpha} \phi({\bf x_n})^T \phi({\bf x_m})
です.
ガウス過程による回帰
本来の観測にはノイズがのります.なので,観測される目的変数の値にノイズを加えた関数を考慮します.
y_n = f_n + \epsilon_n \\
p(y_n|f_n) = N(y_n|f_n,\beta^{-1}) \\
ベクトルで表すと
$$ p({\bf y}|{\bf f}) = N({\bf y}|{\bf f},\beta^{-1} {\bf I}) $$
また,$p({\bf f})$は線形回帰で求めたように平均が${\bf 0}$で共分散が$\bf K$に従うガウス分布です.
$p({\bf y})$を求めたいので周辺化をすると
$$ p({\bf y}) = \int p({\bf y}|{\bf f})p({\bf f}) d{\bf f} = N({\bf y}|{\bf 0}, {\bf K}) $$
です.これが同時確率です.
先ほどのように同時確率➡条件付きガウス分布に変換したいので,
p({\bf y}_{N+1}) = N( {\bf y}_{N+1} | {\bf 0}, {\bf K}_{N+1} )
から
{
{
\begin{bmatrix}
{\bf y}_{1:N} \\ y_{N+1}
\end{bmatrix}
\sim N
\begin{pmatrix}
\begin{bmatrix}
\boldsymbol{\mu}_{1:N}\\ \mu_{N+1}
\end{bmatrix},
\begin{bmatrix}
{\bf K}_N & {\bf k} \\ {\bf k} & k
\end{bmatrix}
\end{pmatrix}
}
}
のように変換します.ここで$ k = k(\bf x_{N+1}, \bf x_{N+1}) + \beta^{-1} $ とします.
すると条件付きガウス分布の章で解説したように,条件付き分布$p(y_{N+1}|\bf y)$は,次に示す平均と共分散を持つようなガウス分布になります.
\begin{align}
p(y_{N+1}|\bf y) & = N(y_{N+1}| m({\bf x}_{N+1}), \sigma^2({\bf x}_{N+1})) \\
m({\bf x}_{N+1}) & = {\bf k}^{\rm T}{\bf K}_N^{-1}{\bf y}_{1:t}, \\
\sigma^2({\bf x}_{N+1}) & = k – {\bf k}^{\rm T}{\bf K}_N^{-1}{\bf k}
\end{align}
となります.この値を用いて獲得関数の更新を行います.
先ほどから$\bf k$が何度か現れていますが,これはカーネル関数と呼ばれるものです.
{\bf k} = [k({\bf x}_{t+1}, {\bf x}_1), k({\bf x}_{t+1}, {\bf x}_2), \cdots, k({\bf x}_{t+1}, {\bf x}_t)]
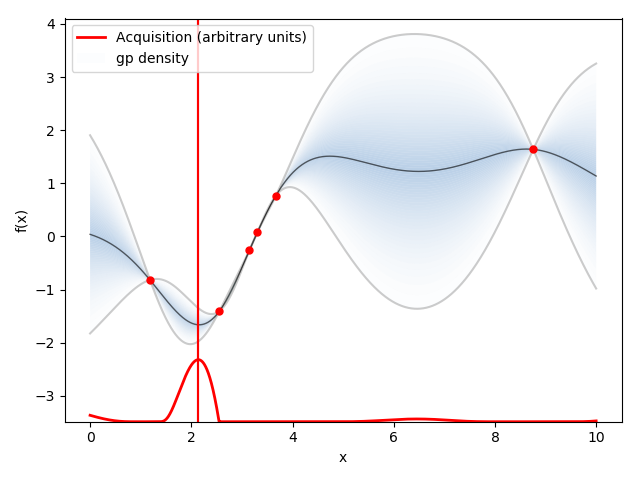
サンプリング10点から周りの他の点$x$における平均・共分散を計算すると以下の図のようになる

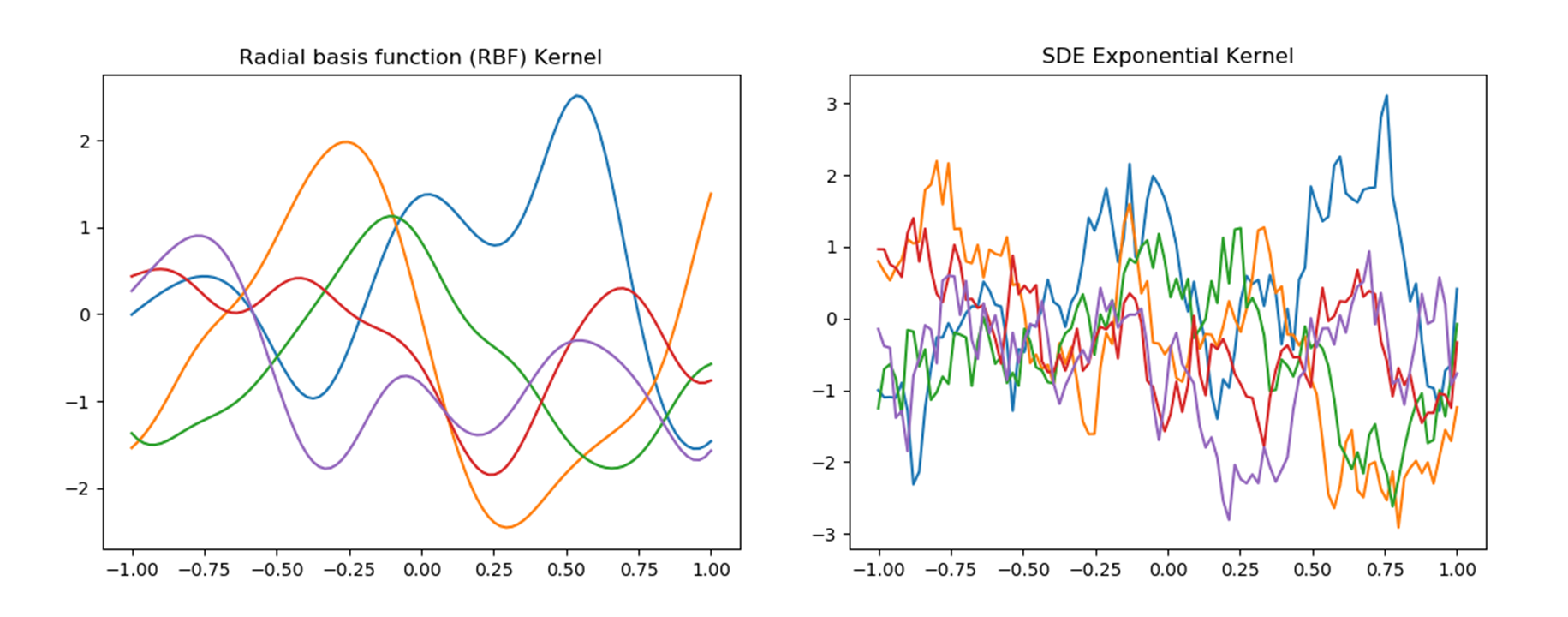
カーネル(核)関数
カーネル関数とは,2つの入力の類似度を測る指標です. 訓練データ点を中心として定義される関数です.(共分散関数とも呼ばれる?)
ここで${\bf x}$と${\bf x}^{\prime}$との「類似度」は,この2点が離れれば離れるだけexponentialで下がっていきます.
つまり,「遠いと似てないよ,近いと似てるね」と表しています.しかし,「類似度」は問題によって変わります.
色々あります.
Squared Exponential Function
$$ k({\bf x}, {\bf x}^{\prime}) = \exp \Bigl( -\frac{1}{2}|| {\bf x} – {\bf x}^{\prime} ||^2 \Bigr) $$
Gaussian Kernel
$$ k({\bf x}, {\bf x}^{\prime}) = \exp \Bigl( - || {\bf x} – {\bf x}^{\prime} ||^2 / 2\sigma^2\Bigr) $$
Ornstein-Uhlenbeck Process
$$ k({\bf x}, {\bf x}^{\prime}) = \exp \Bigl( -\theta | {\bf x} – {\bf x}^{\prime} | \Bigr) $$
PRML第6章ではガウス過程階に用いるカーネル関数として,2次形式の指数をとったものに加え,定数と線形の項を加えたものがよく使われていると述べられています.
$$ k({\bf x}, {\bf x}^{\prime}) = \theta_0 \exp \Bigl( -\frac{\theta_1}{2} || {\bf x} – {\bf x}^{\prime} ||^2 \Bigr) + \theta_2 + \theta_3\bf x^T {\bf x}^{\prime} $$
平均$\bf 0$,共分散$\bf k$でデータを生成したもの(np.random.multivariate_normal(平均, 共分散))を図に示します.
カーネル関数を導入する理由
高次元の特徴空間を1つの関数,カーネル関数を通して間接的に扱うことができるようになることです
多くのパラメトリックな線形モデルは,全く同値な「双対表現」に変換することができます.
***双対表現の意義は,予測モデルが全てカーネル関数$k(\bf x, \bf x')$で表せることです.***常にカーネル関数を通じて問題を扱うことができるため,特徴ベクトル$\phi(\bf x)$を明示的に考えることを避けられます.
例)最小二乗法をカーネルのみで表現すると
$$ f(\bf x) = \bf w^T \bf \phi(\bf x) = \bf k(\bf x)^T (\bf K + \lambda \bf I_N)^{-1} \bf t $$
このようにカーネルで表現すると,$\phi(\bf x)$のような関数よりも高次元の特徴空間を扱い易い(らしいです).
また,カーネル関数は引数$x$に対して対称,すなわち$k(\bf x, \bf x')=k(\bf x', \bf x)$で,かつ半正定値なので,
少ない次元で関数を表現することができるようになります.
※追記
東京大学の鈴木大慈教授によると,カーネル法は,数理最適化手法による高速な学習が可能である.そうです.
獲得関数の更新式の導出
いくつかある獲得関数の中で自分が使おうと思っているExpectation Improvement (EI)についてご紹介します.
獲得関数では「改善」を数値化することを目的とします.
数式で表すと
I(x) = \max(f^*-f(x),0)
ここで$f(x^*)$は現在の最小値,$f$は確率変数$f(x)\sim \mathcal{N}(\mu, \sigma^2)$とします.
ここで$f$は確率変数なので平均を評価するために$I(x)$の期待値をとります.
\begin{align}
EI(x) & = E_{f(x)\sim \mathcal{N}(\mu, \sigma^2)}[I(x)] \\
& = E_{\epsilon\sim \mathcal{N}(0,1)}[I(x)] \\
& = \int_{-\infty}^{\infty} I(x) \phi(\epsilon) d\epsilon \\
& = \int_{-\infty}^{(f^*-\mu)/\sigma} (f^* - \mu - \sigma \epsilon) \phi(\epsilon) d\epsilon \\
& = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) - \sigma \int_{-\infty}^{(f^*-\mu)/\sigma} \epsilon \phi(\epsilon) d\epsilon \\
\end{align}
$\phi(\epsilon)$に$\epsilon \sim\mathcal{N}(0,1)$を代入
$\phi(\epsilon) = \frac{1}{\sqrt{2\pi}} \exp (-\frac{\epsilon^2}{2})$
\begin{align}
EI(x) & = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) + \frac{\sigma}{
\sqrt{2\pi}} \int_{-\infty}^{(f^*-\mu)/\sigma} (-\epsilon) e^{-\epsilon^2/2} d\epsilon \\
& = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) + \frac{\sigma}{
\sqrt{2\pi}} e^{-\epsilon^2/2}|_{-\infty}^{(f^*-\mu)/\sigma} \\
& = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) + \sigma \big(\phi(\frac{f^*-\mu}{\sigma}) - 0\big)\\
& = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) + \sigma \phi(\frac{f^*-\mu}{\sigma})\\
\end{align}
ガウス過程で得られたn+1番目の平均$\mu_{n+1}(x)$と分散$\sigma_{n+1}(x)$を使って以下の獲得関数を更新します.
EI(x) = (f^* - \mu)\Phi(\frac{f^*-\mu}{\sigma}) + \sigma \phi(\frac{f^*-\mu}{\sigma})
まとめと感想
探索(exploration)と搾取(exploitation)のどちらを優先しながら最適解を見つけるアルゴリズムは,かなり強化学習に近いものを感じました.
強化学習は探索を$\epsilon$-greedy手法で,搾取を価値関数や方策勾配法などでより良い解を見つけるわけですが,
ベイズ最適化はベイズ的に理由を持って効率的に探索するのに対し,計算負荷が$\mathcal{O}(n^3)$で増加するため変数が多い複雑な問題には適しません.
強化学習は始めは無駄が多く探索がテキトーですが,ニューラルネットワークを用いていることから少ないパラメータで複雑な関数を表現できるため,複雑な問題でも最適解を求めることができます.
どちらも一長一短ですが,組み合わせたら最強になる可能性があるかもしれません.
| 良い点 | 悪い点 | |
|---|---|---|
| 強化学習 | 複雑な関数を表現可能 | 探索効率が悪い |
| ベイズ最適化 | 探索効率が良い | 計算負荷が$\mathcal{O}(n^3)$ |
@erosionさん、MLPの「ガウス過程と機械学習」によると、ある条件下(等間隔にメッシュ化された空間?)では $\mathcal{O}(n)$で計算できるKISS-GPなる手法があるそうです。
また、制約を考慮したベイズ最適化もあるそうです。(Bayesian Optimization with Inequality Constraints)。めちゃくちゃ研究されてますね、、、、
学習法の分類
また,ニューラルネットワークのように訓練データを使う学習法と比較すると以下のようになります.
ベイズ最適化などは訓練データを予測時に使うため,予測が遅いですが訓練は早いです.
逆にニューラルネットワークは,皆も経験済みの通り訓練は遅いですが,予測は早いです.
学習法の場合も,どちらも一長一短ですが,組み合わせたら最強になる可能性があるかもしれません.
| 良い点 | 悪い点 | |
|---|---|---|
| 訓練データ$\bf t$を使わない・・・ニューラルネットワーク | 予測が早い | 訓練が遅い |
| 訓練データ$\bf t$を使う ・・メモリベース法(ベイズ最適化など) | 予測が遅い | 訓練が早い |
引用
ベイズ最適化の直観的なイメージを得るには
-
アニメーションはベイズ最適化入門を参考にしました
- ベイズ最適化Python ToolであるGPyOptの公式解説Jupyter Notebook

http://ash-aldujaili.github.io/blog/2018/02/01/ei/
https://adtech.cyberagent.io/research/archives/24
PFNでインターンされた方が、高次元空間中でのベイズ最適化についてのブログを書いています。