Go to Qiita Advent Calendar 2024 Top
LoginSignup
6
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

BrainPadAdvent Calendar 2024

Day 17
@wata_f

複数の変数からなる関数の信頼区間を求める【ブートストラップ法&誤差伝搬の法則】

Last updated at Posted at 2024-12-17

はじめに

この記事はBrainpad Advent Calendar 2024の17日目になります。
株式会社ブレインパッドでデータサイエンティストをしているふくだわたるです。

この記事では、複数の変数からなる関数を用いて算出した値の信頼区間を求める方法について、まとめています。
いくつか方法はあるかと思いますが、ここではブートストラップ法で求める方法、誤差伝搬の法則を使う方法について取り上げています。
実務で用いることを念頭に置き、ある施策のABテストを行った結果から売上増加額の信頼区間を求めることを想定して、まとめております。

尚、理論的な説明を行うことを目的とするのではなく、シミュレーションを行った結果の共有を目的としておりますので、理論的な説明は他の記事や書籍を参照いただければと思います。

想定するシチュエーション

本記事ではABテストの結果を関数に当てはめ、求めた値の信頼区間を推定する方法についてまとめます。
具体的なシチュエーションとしては以下のようなものを想定します。

小売業界の施策担当者であるAさんは平均購入金額と購入率に寄与すると考えられる施策（ex.クーポン配布施策）を考案し、実施しました。施策の効果を求めるために、ABテストも実施し、施策がどの程度、平均購入金額と購入率に寄与するのかを算出しました。加えて、Aさんは施策を行ったことで、売上全体に与える影響がどの程度あったのかについても興味があります。また、売上に与える影響がどの程度、信頼に足るものかを確認するために、施策による増加売上額の信頼区間を求めたいと考えています。

変数の確認

ここで本記事で登場する値について確認します。
$R_c$：統制群の売上
$R_t$：処置群の売上
$CVR_c$：統制群の購入率
$CVR_t$：処置群の購入率
$AVG_c$：統制群の平均購入額
$AVG_t$：処置群の平均購入額
$N_c$：統制群に割り当てられた人数
$N_t$：処置群に割り当てられた人数

売上、購入率、平均購入金額は変数となりますが、Nは固定値となります。

また、売上の施策による売上の増加分$\Delta R$は以下の式で求めます。

$$
\Delta R = (R_c + R_t) - (N_c + N_t) \times CVR_c \times AVG_c
$$

右辺の第1項は全体の購入金額を表し、第2項はすべて統制群だった場合の売上（施策を打たなかった場合の売上）と解釈することができます。この差を求めることで、施策による売上の増加分を求めることが可能です。

ABテストのシミュレーション

売上増加額の信頼区間を求めるために、まずABテストのシミュレーションを実施します。以下の値になるようなABテストを設定します。

$CVR_c = 0.45$
$CVR_t = 0.50$
$AVG_c = 600$
$AVG_t = 650$
$N_c = 1000$
$N_t = 5000$

したがって、理論値としては購入率が5%、平均購入金額が50円程度あがる施策を想定します1。

売上増加額の理論値としては、
$$
\Delta R = (R_c + R_t) - (N_c + N_t) \times CVR_c \times AVG_c \
= (270000 + 1625000) - (100 + 500) \times 0.45 \times 600 \
= 275000
$$
となり、施策を行うことで275000円の売上増加が見込まれることを期待します。

import numpy as np
import polars as pl
import scipy.stats as stats
import matplotlib.pyplot as plt
import japanize_matplotlib

# シミュレーションのパラメータ
np.random.seed(42)  # 再現性のためのシード設定
n_control = 1000    # コントロール群のサンプル数
n_test = 5000       # テスト群のサンプル数

# コントロール群のパラメータ
control_purchase_rate = 0.45  # 購入率
control_avg_purchase = 600    # 平均購入金額
control_std_purchase = 100    # 購入金額の標準偏差

# テスト群のパラメータ
test_purchase_rate = 0.50     # 購入率
test_avg_purchase = 650       # 平均購入金額
test_std_purchase = 100       # 購入金額の標準偏差

# 購入データをシミュレーションする関数
def simulate_group(n, purchase_rate, avg_purchase, std_purchase):
    purchase_flag = np.random.binomial(1, purchase_rate, n)
    purchase_amount = purchase_flag * np.random.normal(avg_purchase, std_purchase, n)
    return pl.DataFrame({"purchase_flag": purchase_flag, "purchase_amount": purchase_amount})

# コントロール群とテスト群のデータ作成
control_data = simulate_group(n_control, control_purchase_rate, control_avg_purchase, control_std_purchase)
test_data = simulate_group(n_test, test_purchase_rate, test_avg_purchase, test_std_purchase)

# 購入率の比較
control_purchase_rate_observed = control_data["purchase_flag"].mean()
test_purchase_rate_observed = test_data["purchase_flag"].mean()

# 平均購入金額の比較
control_avg_purchase_observed = control_data.filter(pl.col("purchase_flag") == 1)["purchase_amount"].mean()
test_avg_purchase_observed = test_data.filter(pl.col("purchase_flag") == 1)["purchase_amount"].mean()

# 信頼区間の計算関数
def compute_confidence_interval(data, confidence=0.95):
    mean = np.mean(data)
    sem = stats.sem(data)
    margin = sem * stats.t.ppf((1 + confidence) / 2., len(data) - 1)

    return mean - margin, mean + margin


# 購入率の信頼区間
control_purchase_rate_ci = compute_confidence_interval(control_data["purchase_flag"].to_numpy())
test_purchase_rate_ci = compute_confidence_interval(test_data["purchase_flag"].to_numpy())

# 平均購入金額の信頼区間
control_purchase_amounts = control_data.filter(pl.col("purchase_flag") == 1)["purchase_amount"].to_numpy()
test_purchase_amounts = test_data.filter(pl.col("purchase_flag") == 1)["purchase_amount"].to_numpy()
control_avg_purchase_ci = compute_confidence_interval(control_purchase_amounts)
test_avg_purchase_ci = compute_confidence_interval(test_purchase_amounts)

# 統計的検定
# 購入率の比較 (カイ二乗検定)
purchase_contingency_table = np.array([
    [control_data["purchase_flag"].sum(), n_control - control_data["purchase_flag"].sum()],

    [test_data["purchase_flag"].sum(), n_test - test_data["purchase_flag"].sum()]

])
chi2, p_purchase_rate = stats.chi2_contingency(purchase_contingency_table)[:2]

# 平均購入金額の比較 (t検定)
t_stat, p_avg_purchase = stats.ttest_ind(control_purchase_amounts, test_purchase_amounts)

# 結果の出力
print("=== 購入率の結果 ===")
print(f"コントロール群購入率: {control_purchase_rate_observed:.2%} (95% CI: {control_purchase_rate_ci[0]:.2%} - {control_purchase_rate_ci[1]:.2%})")

print(f"テスト群購入率: {test_purchase_rate_observed:.2%} (95% CI: {test_purchase_rate_ci[0]:.2%} - {test_purchase_rate_ci[1]:.2%})")

print(f"p値: {p_purchase_rate:.4f}")
print("統計的に有意" if p_purchase_rate < 0.05 else "統計的に有意でない")

print("\n=== 平均購入金額の結果 ===")
print(f"コントロール群平均購入金額: {control_avg_purchase_observed:.2f} (95% CI: {control_avg_purchase_ci[0]:.2f} - {control_avg_purchase_ci[1]:.2f})")

print(f"テスト群平均購入金額: {test_avg_purchase_observed:.2f} (95% CI: {test_avg_purchase_ci[0]:.2f} - {test_avg_purchase_ci[1]:.2f})")

print(f"p値: {p_avg_purchase:.4f}")
print("統計的に有意" if p_avg_purchase < 0.05 else "統計的に有意でない")


# 結果を可視化
plt.figure(figsize=(12, 5))

# 購入率の可視化
plt.subplot(1, 2, 1)
groups = ["Control", "Test"]
purchase_rates = [control_purchase_rate_observed, test_purchase_rate_observed]
ci_lower = [control_purchase_rate_ci[0], test_purchase_rate_ci[0]]
ci_upper = [control_purchase_rate_ci[1], test_purchase_rate_ci[1]]
bars = plt.bar(groups, purchase_rates, color=["blue", "orange"], alpha=0.7, yerr=[np.array(purchase_rates) - ci_lower, ci_upper - np.array(purchase_rates)], capsize=5)

plt.ylabel("購入率")
plt.title("購入率の比較")

# 各バーの上に購入率を表示
for bar, rate in zip(bars, purchase_rates):
    yval = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2, yval + 0.02, f'{rate:.2%}', ha='center', va='bottom')  

# 平均購入金額の可視化
plt.subplot(1, 2, 2)
mean_purchases = [control_avg_purchase_observed, test_avg_purchase_observed]
ci_lower = [control_avg_purchase_ci[0], test_avg_purchase_ci[0]]
ci_upper = [control_avg_purchase_ci[1], test_avg_purchase_ci[1]]
bars = plt.bar(groups, mean_purchases, color=["blue", "orange"], alpha=0.7, yerr=[np.array(mean_purchases) - ci_lower, ci_upper - np.array(mean_purchases)], capsize=5)

plt.ylabel("平均購入金額")
plt.title("平均購入金額の比較")

# 各バーの上に平均購入金額を表示
for bar, amount in zip(bars, mean_purchases):
    yval = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2, yval + 5, f'{amount:.2f}', ha='center', va='bottom')  

plt.tight_layout()
plt.show()


# 売上増加額の理論値
control_revenue = control_purchase_rate * control_avg_purchase * n_control
test_revenue = test_purchase_rate * test_avg_purchase * n_test
expected_revenue = (control_revenue + test_revenue) - (n_control + n_test) * control_purchase_rate * control_avg_purchase

print(f"\n理論的な売上増加額: {expected_revenue:.2f}")

# 売上増加額の観測値
control_revenue_observed = control_data["purchase_amount"].sum()
test_revenue_observed = test_data["purchase_amount"].sum()
observed_revenue = (control_revenue_observed + test_revenue_observed) - (n_control + n_test) * control_purchase_rate_observed * control_avg_purchase_observed
print(f"観測された売上増加額: {observed_revenue:.2f}")

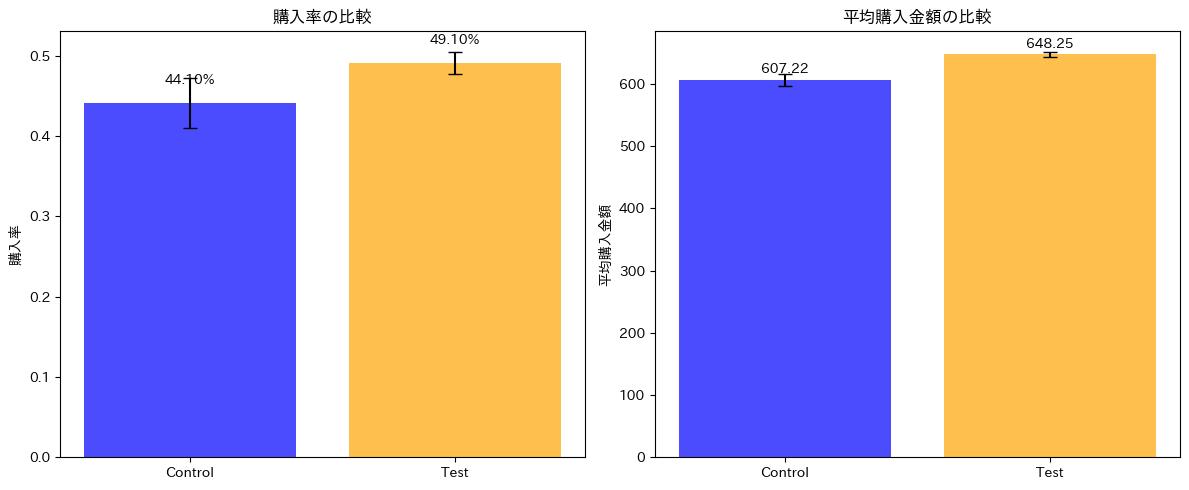
上記コードを実行すると、ABテストのシミュレーションが実行され、信頼区間も算出されます。
購入率、平均購入金額ともに有意な結果が得られていることが確認できます。
また、観測された売上増加額は252541.24円となり、若干理論値よりも低い値が算出されました。

image.png

売上増加額の信頼区間（ブートストラップ法）

それでは、いよいよ売上増加額の95%信頼区間を算出したいと思います。
まず、ブートストラップ法で売上増加額の信頼区間を算出します。
ブートストラップ法はデータの再サンプリングを行い、統計量の分布を推定する手法で、データの分布に関する仮定が少ないといった利点があります。なにより、シンプルなため、今回のようなケースで信頼区間を求める際には、最初に思いつく手法なのではないかと思います。

ABテストのコードに下記のコードを加えるとブートストラップ法による売上増加額の信頼区間を求めることができます。

np.random.seed(42)  # 再現性のためのシード設定


# ブートストラップ法による信頼区間の計算
def bootstrap_confidence_interval(control_data, test_data, num_samples=n_control+n_test, confidence=0.95):
    bootstrapped_means = []
    for _ in range(num_samples):
        sample_control_indices = np.random.choice(control_data.shape[0], size=n_control, replace=True)
        sample_test_indices = np.random.choice(test_data.shape[0], size=n_test, replace=True)
        
        sample_control = control_data[sample_control_indices]
        sample_test = test_data[sample_test_indices]
        
        control_revenue = sample_control["purchase_amount"].sum()
        test_revenue = sample_test["purchase_amount"].sum()
        
        control_purchase_rate_sample = sample_control["purchase_flag"].mean()
        control_avg_purchase_sample = sample_control.filter(pl.col("purchase_flag") == 1)["purchase_amount"].mean()
        
        increase_revenue = (control_revenue + test_revenue) - (n_control + n_test) * control_purchase_rate_sample * control_avg_purchase_sample


        bootstrapped_means.append(increase_revenue)
    
    lower_bound = np.percentile(bootstrapped_means, (1 - confidence) / 2 * 100)

    upper_bound = np.percentile(bootstrapped_means, (1 + confidence) / 2 * 100)
    return lower_bound, upper_bound

# 増加売上金額の信頼区間
increase_revenue_ci = bootstrap_confidence_interval(control_data, test_data)

# 統制群の売上
control_revenue = control_data["purchase_flag"].sum() * control_avg_purchase

# 介入群の売上
test_revenue = test_data["purchase_flag"].sum() * test_avg_purchase

# 増加売上金額の計算
increase_revenue = (control_revenue + test_revenue) - (n_control + n_test) * control_purchase_rate * control_avg_purchase


print(f"増加売上金額: {increase_revenue:.2f}")
print(f"増加売上金額の95%信頼区間: {increase_revenue_ci[0]:.2f} - {increase_revenue_ci[1]:.2f}")

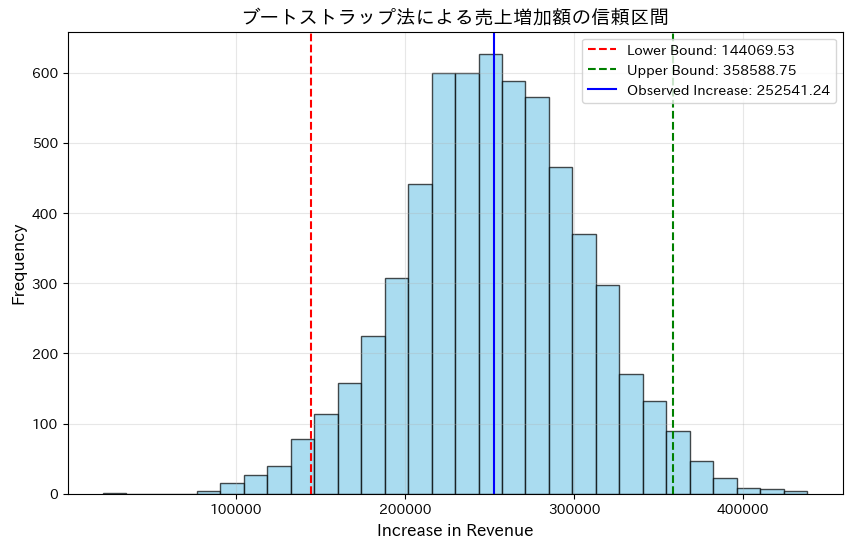
結果は以下のようになります。
下限値が144069.53円、上限値が358688.75円となり、20万円程度の信頼区間の幅ということになります。
理論値である275000円が信頼区間に含まれていることから一定、妥当性のある結果になっていることがわかるかと思います。

image.png

売上増加額の信頼区間（誤差伝搬の法則）

次に誤差伝搬の法則を用いて、関数全体の標準誤差を求めることで信頼区間を求めてみます。
誤差伝搬の法則についてこちらのQitta記事に詳しく書かれていました。
https://qiita.com/yusuke_s_yusuke/items/6222d8565cb22d51051f

誤差伝搬の法則を用いて、売上増加額の標準誤差を求めるには各変数の標準誤差を求める必要があります。
各変数の標準誤差は以下のようになります。

$SE_{R_c} = \sqrt{\sum_{i=1}^{N_c} \sigma_{AVG_c}^2} = \sqrt{N_c} \times \sigma_{AVG_c} $
$ SE_{R_t} = \sqrt{\sum_{i=1}^{N_t} \sigma_{A_t}^2} = \sqrt{N_t} \times \sigma_{A_t} $
$ SE_{CVR_c} = \sqrt{\frac{CVR_c \times (1 - CVR_c)}{N_c}}$
$ SE_{A_c} = \frac{\sigma_{AVG_c}}{\sqrt{N_c}} $

各変数の標準誤差を用いて、関数全体の標準誤差を以下の式で近似して求めます。

$ SE_{\Delta R} = \sqrt{SE_{R_c}^2 + SE_{R_t}^2 + \left((N_c + N_t) \times AVG_c \times SE_{CVR_c}\right)^2 + \left((N_c + N_t) \times CVR_c \times SE_{AVG_c}\right)^2}$

この式が成り立つためにはいくつかの仮定が必要です。
代表的なものは以下2つです。

  • 各変数は互いに独立である
  • 各変数の標準誤差は、正規分布に従う

今回は上記の式で算出された標準誤差を用いて信頼区間を推定します。

# 各変数の標準誤差を計算
control_revenue_se = np.sqrt(control_data["purchase_flag"].sum()) * control_std_purchase
test_revenue_se = np.sqrt(test_data["purchase_flag"].sum()) * test_std_purchase
control_cvr_se = np.sqrt(control_purchase_rate * (1 - control_purchase_rate) / n_control)

control_avg_purchase_se = control_std_purchase / np.sqrt(n_control)

# 誤差伝搬法による増加売上金額の標準誤差の計算
increase_revenue_se = np.sqrt(
    control_revenue_se**2 +
    test_revenue_se**2 +
    ((n_control + n_test) * control_avg_purchase * control_cvr_se)**2 +
    ((n_control + n_test) * control_purchase_rate * control_avg_purchase_se)**2
)

# 信頼区間の計算
confidence_level = 0.95
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)

ci_lower = increase_revenue - z_score * increase_revenue_se

ci_upper = increase_revenue + z_score * increase_revenue_se

print(f"増加売上金額: {increase_revenue:.2f}")
print(f"増加売上金額の95%信頼区間: {ci_lower:.2f} - {ci_upper:.2f}")

上記のコードを用いて、信頼区間を求めたところ、139788.61、365293.86という結果になりました。
若干、ブートストラップ法により、信頼区間が広まったことがわかります。
誤差伝搬の法則についても、理論値である275000円が信頼区間に含まれており、一定妥当性のある結果になっているといえます。

まとめ

今回はブートストラップ法と誤差伝搬の法則を用いて売上増加額の信頼区間を求めました。今回のシミュレーションでは、ブートストラップ法による方法の方が、信頼区間がせまくなるという結果になりましたが、誤差伝搬の法則による方法の方が、信頼区間がせまくなることもあるようです。また、誤差伝搬の法則で推定方法はブートストラップ法による方法と比較し、結果をより早く推計しやすいといったメリットがあります。しかし、ブートストラップ法による方法と比較し、誤差伝搬の法則は必要とする仮定が多いといった使いにくさがあります。必要に応じて、使い分けることが重要そうです。

参考

  1. わかりやすさのために、かなり効果の大きい施策を想定しました ↩

6
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?