はじめに
誤差伝搬の法則は、複数の変数からなる関数の誤差を計算するための法則である。この法則は、ある関数が複数の変数に依存している場合に、それぞれの変数の誤差がその関数に与える誤差を理解するのに役立つ。
例えば、観測機器を使用して測定を行う際に、多かれ少なかれ誤差が含まれることはよくあり、誤差伝搬の法則は、これらの誤差が最終的な結果に含まれる誤差を解析的に計算するために使われる。
本記事では、まず2変量からなる関数の誤差の伝搬について導出する。続いて、多変数での誤差伝搬の法則へと一般化する。最後に、誤差伝搬の定性的なイメージを図を使って説明する。
2変数での誤差伝搬の法則
簡単のため、まず2変数での誤差伝搬の式について説明する。誤差を含まない真の2変数$x$、$y$からなる関数を
z = f(x, y)\tag{1}
とする。測定ごとの誤差を$\Delta x$、$\Delta y$とすると、変数$z$の誤差は
z+\Delta z = f(x+\Delta x, y+\Delta y)\tag{2}
と表される。
この式を1次の項までテイラー展開すると
f(x+\Delta x, y+\Delta y)\sim f(x,y)+\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y\tag{3}
となる。式$(2)$、$(3)$より、
\begin{aligned}
\Delta z&=f(x+\Delta x, y+\Delta y)-f(x, y)\\
&= \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y
\end{aligned}
\tag{4}
を得る。
$\Delta x,~\Delta y,~\Delta z$は、正負に値が現れるため、誤差の見通しが良くない。そこで、2乗をとると
\begin{aligned}
(\Delta z)^2 &= \left(\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y\right)^2\\
&= \left(\frac{\partial f}{\partial x}\right)^2(\Delta x)^2 + \left(\frac{\partial f}{\partial y}\right)^2(\Delta y)^2 + 2\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\Delta x\Delta y
\end{aligned}
\tag{5}
となる。
ここで、$z$についての誤差の期待値を求める。$n$回測定したとすると、$(x^{(1)},x^{(2)},\dots, x^{(n)})$、$(y^{(1)},y^{(2)},\dots, y^{(n)})$のように、$n$個分のデータを得ることになる。(次セクションの多次元の場合との混同を避けるため、$x^{(1)}$のように変数の上に添え字を書いたが、累乗という意味ではない。)
こうした測定データから、統計的に$(\Delta x)^2$、$(\Delta y)^2$、$\Delta x\Delta y$の期待値を得ることができる。各誤差の期待値$\mathbb E$は
\begin{aligned}
\mathbb E[(\Delta x)^2]&= \frac{1}{n}\sum_{i=1}^n (x^{(i)}-x)^2=\frac{1}{n}\sum_{i=1}^n (\Delta x^{(i)})^2=\sigma_x^2 \\
\mathbb E[(\Delta y)^2]&= \frac{1}{n}\sum_{i=1}^n (y^{(i)}-y)^2=\frac{1}{n}\sum_{i=1}^n (\Delta y^{(i)})^2=\sigma_y^2\\
\mathbb E[\Delta x\Delta y] &= \frac{1}{n}\sum_{i=1}^n (x^{(i)}-x)(y^{(i)}-y)=\frac{1}{n}\sum_{i=1}^n \Delta x^{(i)}\Delta y^{(i)}=\sigma_{x,y}\\
\end{aligned}
\tag{6}
と表される。いわゆる、$\sigma_x^2,~\sigma_y^2$は分散、$\sigma_{x,y}$は共分散として知られている。これらの式$(6)$を$(5)$に代入して、$\Delta z$の期待値$\mathbb E[(\Delta z)^2]=\sigma_z^2$を求めると
\sigma_z^2 =\left(\frac{\partial f}{\partial x}\right)^2\sigma_x^2 + \left(\frac{\partial f}{\partial y}\right)^2\sigma_y^2 + 2\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\sigma_{x,y}
\tag{7}
となる。この式$(7)$を2変数での誤差伝搬の法則という。
式$(7)$に相関係数($xy$間の共分散/$x$の標準偏差と$y$の標準偏差の積で定義される)
r_{x,y}\equiv\frac{\sigma_{x,y}}{\sigma_x\sigma_y}~ \rightarrow ~\sigma_{x,y}=r_{x,y}{\sigma_x\sigma_y}
\tag{8}
を代入して
\sigma_z^2 =\left(\frac{\partial f}{\partial x}\right)^2\sigma_x^2 + \left(\frac{\partial f}{\partial y}\right)^2\sigma_y^2 + 2\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}r_{x,y}{\sigma_x\sigma_y}
\tag{9}
と表すこともある。変数間の関係は相関係数を使うと読み取りやすくなることも多い。
特に、$x,~y$が独立のとき、$\sigma_{x,y}=0$($r_{x,y}=0$)であり、式$(9)$は
\sigma_z^2 = \left(\frac{\partial f}{\partial x}\right)^2\sigma_x^2 + \left(\frac{\partial f}{\partial y}\right)^2\sigma_y^2
\tag{10}
となる。
誤差伝搬の法則の一般形
ここで、多変数の場合へと一般化する。多変数$x_1, \dots, x_n$からなる関数$z=f(x_1, \dots, x_n)$について、多変量テイラー展開を1次の項まで書き下すと
f(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\sim f(x_1,\dots,x_n)+\frac{\partial f}{\partial x_1}\Delta x_1+\cdots +\frac{\partial f}{\partial x_n}\Delta x_n\tag{11}
となる。誤差$\Delta z$は
\begin{aligned}
\Delta z&=f(x_1+\Delta x_1,\dots,x_n+\Delta x_n)-f(x_1,\dots,x_n)\\
&= \frac{\partial f}{\partial x_1}\Delta x_1+\cdots + \frac{\partial f}{\partial x_n}\Delta x_n
\end{aligned}
\tag{12}
となる。この式$({12})$を2乗すると、
\begin{aligned}
(\Delta z)^2&=\left(\frac{\partial f}{\partial x_1}\Delta x_1+\cdots + \frac{\partial f}{\partial x_n}\Delta x_n\right)^2\\
&=\left(\frac{\partial f}{\partial x_1}\right)^2(\Delta x_1)^2+\left(\frac{\partial f}{\partial x_2}\right)^2(\Delta x_2)^2+\cdots +\left(\frac{\partial f}{\partial x_n}\right)^2(\Delta x_n)^2\\
&\quad+2\frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}\Delta x_1\Delta x_2+2\frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_3}\Delta x_1\Delta x_3+\cdots+2\frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_n}\Delta x_1\Delta x_n\\
&\quad+2\frac{\partial f}{\partial x_2}\frac{\partial f}{\partial x_3}\Delta x_2\Delta x_3+2\frac{\partial f}{\partial x_2}\frac{\partial f}{\partial x_4}\Delta x_2\Delta x_4+\cdots+2\frac{\partial f}{\partial x_2}\frac{\partial f}{\partial x_n}\Delta x_2\Delta x_n\\
&\quad+2\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_{i+1}}\Delta x_i\Delta x_{i+1}+2\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_{i+2}}\Delta x_{i}\Delta x_{i+2}+\cdots+2\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_n}\Delta x_i\Delta x_n\\
&\quad+\cdots+2\frac{\partial f}{\partial x_{n-1}}\frac{\partial f}{\partial x_n}\Delta x_{n-1}\Delta x_n\\
&=\sum_{k=1}^n \left(\frac{\partial f}{\partial x_k}\right)^2(\Delta x_k)^2 + 2 \sum_{1 \leq i < j \leq n}\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_j}\Delta x_i\Delta x_j
\end{aligned}
\tag{13}
となる。ここで、$\sum_{1 \leq i < j \leq n}$は、全ての変数間同士の和を表し、具体的には$i$に対して$j$が常に大きいような添え字の選び方をした和をとることを意味する。例えば4変数の場合、$(i,j)=(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)$となる。
$(\Delta z)^2$の期待値$\sigma_z$は、分散と共分散を用いて
\sigma_z^2 =\sum_{k=1}^n \left(\frac{\partial f}{\partial x_k}\right)^2\sigma_{{x}_{k}}^2 + 2 \sum_{1 \leq i < j \leq n}\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_j}\sigma_{x_i,x_j}
\tag{14}
と表される。この式$(14)$は一般化された誤差伝搬の法則である。
相関係数$(8)$を用いると式$(14)$は、
\sigma_z^2 =\sum_{k=1}^n \left(\frac{\partial f}{\partial x_k}\right)^2\sigma_{{x}_{k}}^2 + 2 \sum_{1 \leq i < j \leq n}\frac{\partial f}{\partial x_i}\frac{\partial f}{\partial x_j}r_{x_i,x_j}\sigma_{x_i}\sigma_{x_j}
\tag{15}
特に、変数が全て独立であるとき$\sigma_{x_ix_j}=0$($r_{x_ix_j}=0$)を満たし、単に
\sigma_z^2 = \sum_{k=1}^n \left(\frac{\partial f}{\partial x_k}\right)^2\sigma_{{x}_{k}}^2
\tag{16}
と表される。
定性的なイメージ
ここでは、図などを用いることで誤差伝搬の式を定性的なイメージを説明する。簡単のため2変数$x,~y$からなる関数$z=f(x,y)=x+y$を例にとって考える。
図示による説明
$z=f(x,y)=x+y$のとき、誤差伝搬の法則より、
\begin{aligned}
\sigma_z^2 &= \sigma_x^2+\sigma_y^2+2\sigma_{x,y}\\
&= \sigma_x^2+\sigma_y^2+2r_{x,y}\sigma_{x}\sigma_{y}\\
\end{aligned}
となる。$\sigma_z^2$の平方根をとり標準偏差$\sigma_z$を求めると
\sigma_z = \sqrt{\sigma_x^2+\sigma_y^2+2r_{x,y}\sigma_{x}\sigma_{y}}
となる。
簡単のため、まずは相関係数$r_{x,y}=0$の場合について、横軸に$\sigma_x$、縦軸に$\sigma_y$をとり図示すると
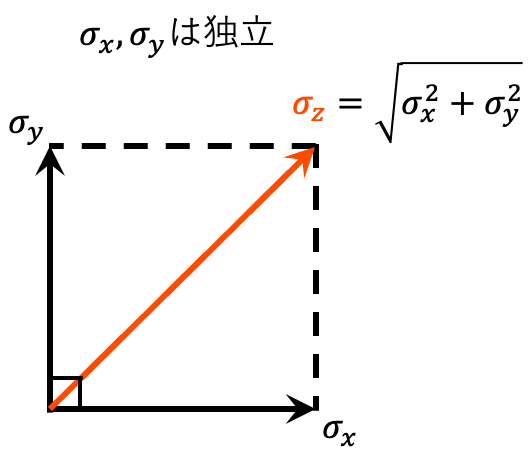
となる。このように、直行関係にある。
次に、$r_{x,y}\neq0$の場合について図示する。例えば、$\sigma_x,~\sigma_y$が正の相関がある場合、
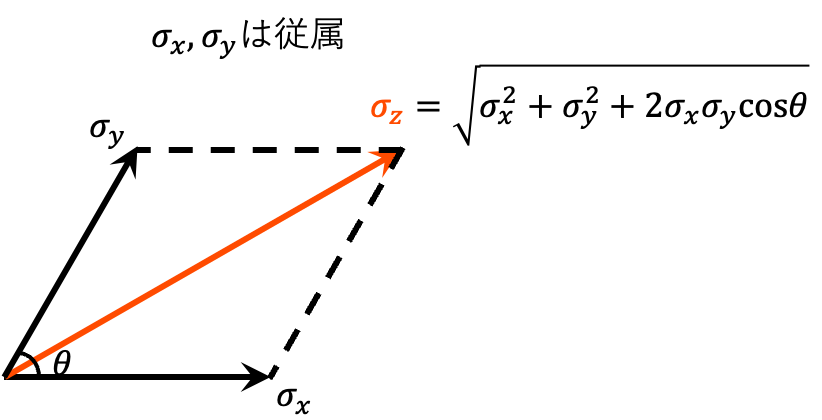
と表すことができる。ここで、$\theta$は$\sigma_x,~\sigma_y$間のなす角である。
成分分解して計算すると、
\begin{aligned}
\sigma_z &= \sqrt{(\sigma_x+\sigma_y\cos\theta)^2+\sigma_y^2\sin^2\theta}\\
&= \sqrt{\sigma_x^2+2\sigma_x\sigma_y\cos\theta+\sigma_y^2\cos^2\theta+\sigma_y^2\sin^2\theta}\\
&= \sqrt{\sigma_x^2+\sigma_y^2+2\sigma_x\sigma_y\cos\theta}
\end{aligned}
となる。つまり、この図で$\cos\theta=r_{x,y}$の対応関係にある。ただし、図示はあくまで2変数の場合の説明であることに注意する。多変数ではより複雑になるはずである(私は3次元以上はイメージが湧かない)。
従属性の定性的な説明
$z=f(x,y)=x+y$の標準偏差$\sigma_z$は先と同様に
\sigma_z=\sqrt{\sigma_x^2+\sigma_y^2+2r_{x,y}\sigma_{x}\sigma_{y}}
と表される。この第3項($r_{x,y}\sigma_{x}\sigma_{y}$)についての定性的なイメージを考える。
- $r_{x,y}=0$のとき: $\sigma_x,~\sigma_y$に相関がないので、測定量は$x,~y$を中心として正と負に適当に現れる。このため、その$\Delta x,~\Delta y$の平均的な量はゼロになる。
- $r_{x,y}>0$のとき: $\sigma_x,~\sigma_y$に正の相関があるので、$\Delta x>0$のときは$\Delta y>0$が出やすく、逆に$\Delta x<0$のときは$\Delta y<0$が出やすい。そのため、同符号が出やすいことから、$\Delta x\Delta y$の平均的な量は正になる。
- $r_{x,y}<0$のとき: $\sigma_x,~\sigma_y$に負の相関があり、$r_{x,y}>0$の説明の逆になる。つまり、$\Delta x,~\Delta y$は異符号である傾向にあり、$\Delta x\Delta y$の平均的な量は負になる。
実際に、$z=x+y$について、相関関係による$\sigma_z$の大小関係をみると
\sigma_z(負の相関)<\sigma_z(独立)<\sigma_z(正の相関)
これは一つ前のセクションの図示による説明と絡めると理解しやすい。負の相関のとき、$\Delta
_x,~\Delta_y$は打ち消し合う方向にベクトルが向くので、$z$の誤差も小さくなる。逆に、正の相関のとき、ベクトル同じ方向に向き強め合うので$z$の誤差が大きくなる。
まとめ
この記事では、誤差伝搬の法則について解説した。この法則は、複数の変数からなる関数の誤差を計算する際に利用され、測定や観測における誤差の影響を理解するのに役立つ。2変数と多変数の場合における誤差伝搬の導出を紹介し、相関係数の影響についても考察した。
誤差伝搬の法則は科学や工学分野で幅広く応用され、正確なデータ解釈や実験計画において不可欠なツールであり、本記事が理解を深める一助になれば幸いである。
最後に、誤差伝搬の法則のシミュレーションの記事も書いているので宜しければ
も合わせてご覧ください。
参考記事