Google Colaboratory を使ってお手軽に数学 gif を作ってみよう

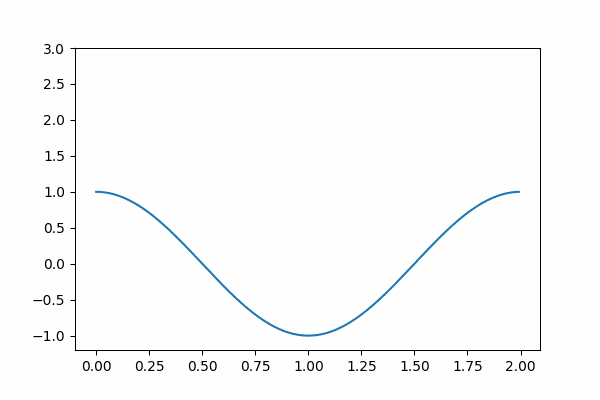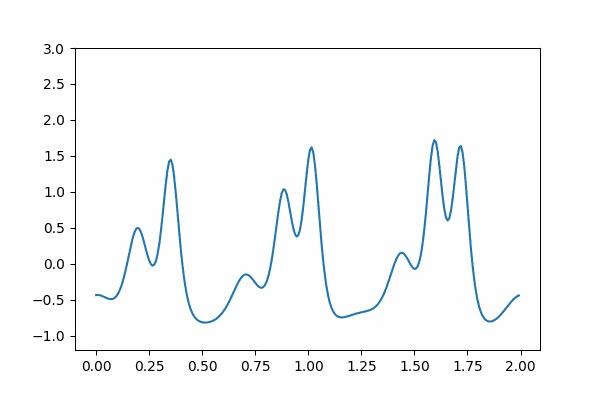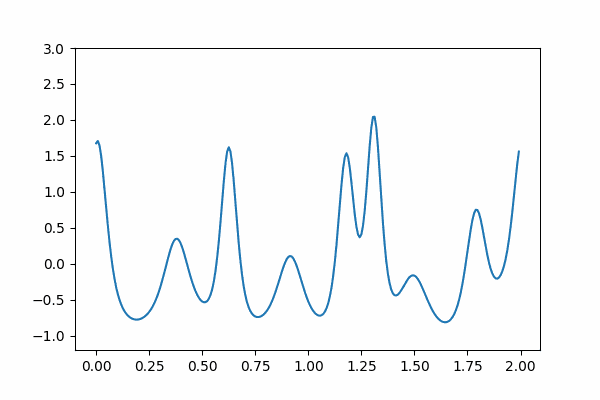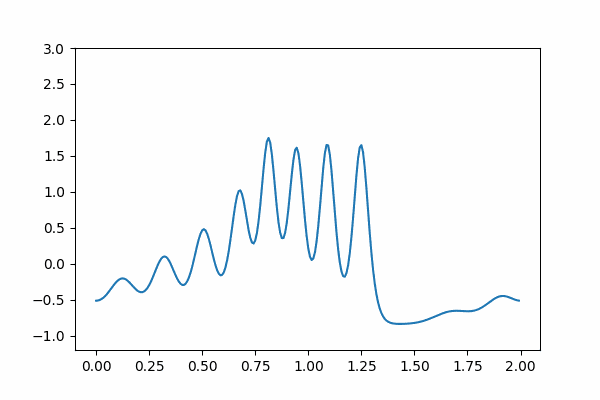
本記事では Google Colaboratory で数学 gif を作ります. 非線形波動を記述するコルトヴェーグ・ドフリース方程式を数値計算により解いてソリトンが現れることを見ていきましょう.

1. Google Colaboratory を使おう

Google Colaboratory を使えば, 自分の PC に何もインストールすることなく(インターネット接続さえできれば) Python をノートブック形式で扱うことができます.

過去記事 [Python を使ってお手軽に数学 gif を作ってみよう - @wakabame][1] では環境構築の手順がありましたが, これが不要になります.
コードの実行も Google のクラウドサーバー上で行われるため, 無料で計算資源を使うことができます.

他にも特徴があるため, 詳しくは公式のドキュメントを参考にしましょう.
https://colab.research.google.com/notebooks/welcome.ipynb?hl=ja

2. コルトヴェーグ・ドフリース方程式の数値計算をしよう

この節は [擬スペクトル法によるKdV方程式の数値計算 -- とつとつとしてろうとせず][2] を参考にしました.

コルトヴェーグ・ドフリース方程式と呼ばれる, 浅水波の高さ $u$ の動きを記述する初期値境界値問題
$$
\begin{cases}
&u_t + \alpha u u_x + \beta u_{xxx} = 0, \quad & t>0, x \in (0, L),\\
&u(t,0) = u(t,L),\quad &t>0,\\
&u(0,x) = u_0(x), \quad &x \in (0,L)
\end{cases}
$$
を考えます.
ここで $L$, $\alpha$, $\beta$ は正の定数で, ザブスキー・クルスカルが孤立波を発見した際のパラメータ $L=2.0$, $\alpha = 1.0$, $\beta = 0.022^2$ であるとし, 初期値は $u_0(x) = \cos(\pi x)$ により与えられるものとします.

数値計算においては空間方向について scipy.fftpack の diff を用いて $u_x$, $u_{xxx}$ をフーリエ変換により求めます.
一方で時間方向には離散化を行い scipy.integrate の solve_ivp を用いて陰的ルンゲ・クッタ法により次のタイムステップ時刻における数値解を求めていきます.

必要なライブラリのインポート

import numpy as np
from numpy import pi, cos, linspace, arange
from numpy.fft import rfft, irfft
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
from scipy.integrate import solve_ivp
from scipy.fftpack import diff as psdiff

パラメータと初期値の設定

# Constant in Zabusky & Kruskal (1965)
DELTA = 0.022 ** 2
L = 2.0 # width of line domain

N = 256 # step width for spatial variable
T = 10 # last time
dt = 1.0e-2 # step width for time variable

# initial condition
x = linspace(0.0, L, N, endpoint=False)
u0 = cos(pi*x)

フーリエ変換を用いた $u_t$ の計算

def kdv(t, u):
    conv = u * psdiff(u, period=L)
    disp = DELTA * psdiff(u, period=L, order=3)
    dv = - conv - disp
    return dv

陰的ルンゲクッタ法による数値解の計算

t = np.arange(0, T, dt)
sol = solve_ivp(kdv, [0, T], u0, method='Radau', t_eval=t)

3. 可視化しよう

この節は, [Google Colaboratory上で勾配降下法を可視化する - @yaju][3] を参考にしました.

数値解の準備

得られた解 sol.y は[空間][時間]の順に並ぶ二次元配列なので, 転置して U[t][x] となるようにしておきます.

U = sol.y.T
frames = len(U)

notebook での可視化

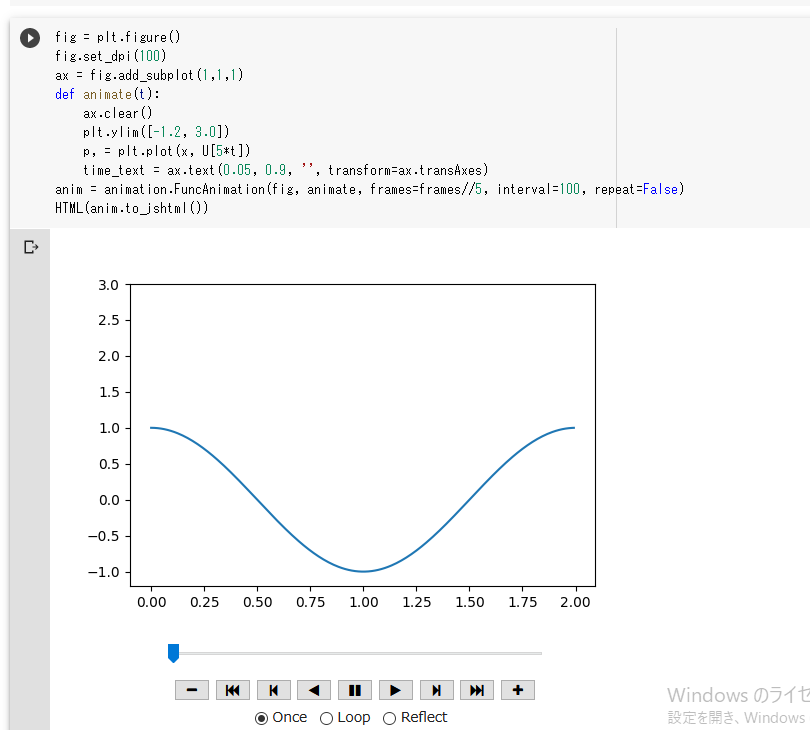
ノートブックで可視化する際には, IPython.display の HTML から確認すると見やすいです.
ただし, Colaboratory 上では一つのセルでメモリを大量に消費すると接続が切られる仕様になっている（？）ため, gifのフレームを200くらいに収まるように間引きます.

%matplotlib inline
fig = plt.figure()
fig.set_dpi(100)
ax = fig.add_subplot(1,1,1)
def animate(t):
    ax.clear()
    plt.ylim([-1.2, 3.0])
    p, = plt.plot(x, U[5*t])
anim = animation.FuncAnimation(fig, animate, frames=frames//5, interval=100, repeat=False)
HTML(anim.to_jshtml())

gifファイルの書き出し

gifファイルを書きだす際には, writer="pillow" のオプションによりほとんど手を加えずに出力することができます.
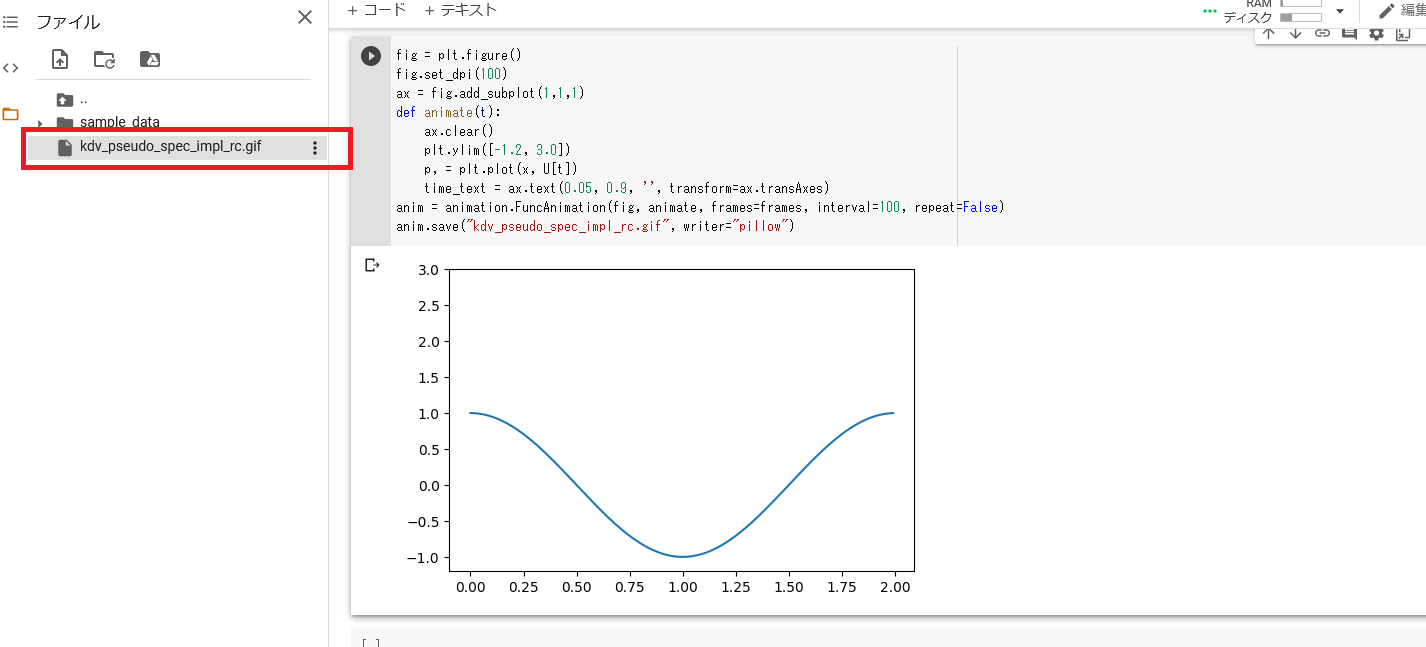
書き出しが完了すると, 左側のタブを開くことでgifファイルがドライブ上に保存されているのが見つかるので, 右クリックしてダウンロードしましょう

fig = plt.figure()
fig.set_dpi(100)
ax = fig.add_subplot(1,1,1)
def animate(t):
    ax.clear()
    plt.ylim([-1.2, 3.0])
    p, = plt.plot(x, U[5*t])
anim = animation.FuncAnimation(fig, animate, frames=frames//5, interval=100, repeat=False)
anim.save("kdv_pseudo_spec_impl_rc.gif", writer="pillow")

今回のノートブックは kdv.ipynb にて公開しています.
コメント等ございましたらよろしくお願いします.
[1]:https://qiita.com/wakabame/items/c3648501eb0f2b921ddf
[2]:https://iqujack-lequina.hatenablog.com/entry/2018/05/02/%E6%93%AC%E3%82%B9%E3%83%9A%E3%82%AF%E3%83%88%E3%83%AB%E6%B3%95%E3%81%AB%E3%82%88%E3%82%8BKdV%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%81%AE%E6%95%B0%E5%80%A4%E8%A8%88%E7%AE%97
[3]:https://qiita.com/yaju/items/42d43d6d6cf6910e8701