概要
本稿では,有限体と拡大体を説明し,ガロア体$\ GF(2^4)\ $をPythonで実装します.その上で,$\ GF(2^4)\ $上でのElGamal暗号も実装します.
有限体について
素数$\ p\ $個の元をもつ次のような集まりは,有限体$\ \mathbb{F}_p\ $です.
\mathbb{F}_p = \{ 0, 1, \cdots, p-1\}.
この集合には,たし算とかけ算が定義されており,例えば$\ p=5\ $のとき,
2 + 3 = 0, \ \ 1 + 3 = 4,\ \ 3 + 4 = 2,\\
2 \times 3 = 1,\ \ 1 \times 3 = 3,\ \ 3 \times 4 = 2.
$a,b \in \mathbb{F}_p\ $に対して,次のように計算することに注意してください.
a + b \pmod{p},\\
a \times b \pmod{p}.
ポイントは,「元の個数が素数である」ということです.それを詳しく説明するために,有限体とよく似ている剰余環(じょうよかん)$\mathbb{Z}/p\mathbb{Z}\ $と$\ \mathbb{Z}/n\mathbb{Z}\ $に登場してもらいます.ただし,$p\ $は素数で,$n\ $は素数でない合成数とします.剰余環は,難しそうな名前ですが,次のようなものです.
\mathbb{Z}/p\mathbb{Z} = \{ 0, 1, \cdots, p-1\},\\
\mathbb{Z}/n\mathbb{Z} = \{ 0, 1, \cdots, n-1\}.
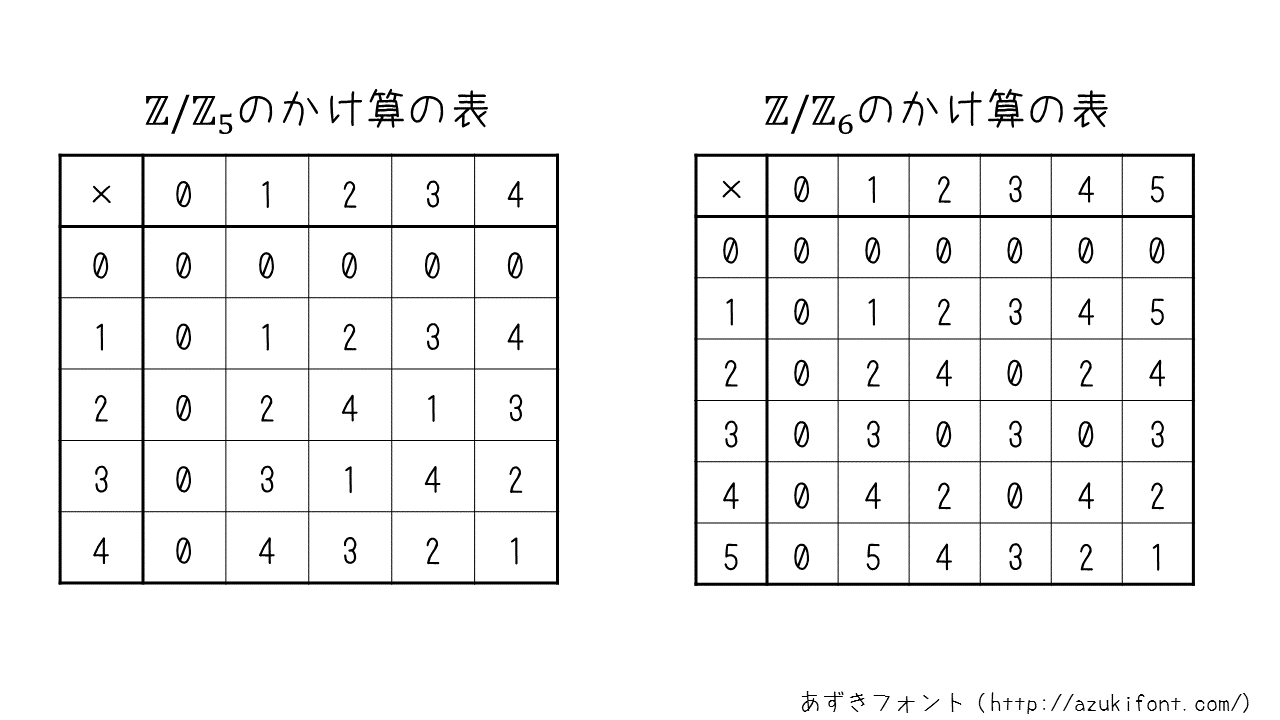
これらにも,たし算とかけ算が定義されています.そこで,$p=5, n=6\ $の場合の「かけ算の表」を書いてみましょう.
この表より,2つの剰余環の違いがなんとなくわかったのではないでしょうか.それは元の個数が素数である剰余環では,$0\ $を使わなければかけ算の結果が$\ 0\ $にならないということです.したがって,何回もかけ算するなど暗号に代表される複雑な計算によって,暗号化や復号などの意味ある計算が$\ 0\ $の出現のために無意味になるかもしれないという心配はいりません.代数学では,「元の個数が素数である剰余環」を「有限体」と呼び,暗号学ではこれを重宝します.例えば,$\mathbb{F}_{23}\ $の場合,
\textbf{a} = \{ 2^j : j\in \{0,1,\cdots, 11\}\}.
拡大体について
先ほどの議論では元の個数が合成数の場合,有限体はつくれませんでした.事実,$n = 2^4$の場合,
2\times 8 = 0, 4\times4=0.
ただ,合成数の場合でも既約多項式を用いることによって有限体をつくることができます.既約多項式とは,これ以上分解できない多項式のことです.例えば,
x^4 + x + 1 は既約多項式ですが,\\
x^4 + 1 \ はそうではありません
なぜならば,各係数は$\ \{ 0, 1\}\ $なので,
x^4 + 1 = x^4 + 2x^2 + 1 = (x^2 + 1)^2.
それでは,有限体をつくっていきます.既約多項式でつくる方程式:$x^4 + x+1 = 0\ $の解を$\ \alpha \ $とするとき,
\textbf{a} = \{ \alpha^j : j\in \{0,1,\cdots, 2^4-2\}\}
は,すべて異なる元の集まりです.まずこれ以上分解できないことから次の4つの元はそれぞれ異なります.
\alpha^0, \alpha^1, \alpha^2, \alpha^3.
その他は,$\alpha^4 + \alpha+1 = 0\ $を用いることによって確かめることができます.
\alpha^4 = \alpha + 1,\ \alpha^5 = \alpha^2 + \alpha, \ \alpha^6 = \alpha^3 + \alpha^2,\ \alpha^7 = \alpha^3 + \alpha + 1,\\
\alpha^8 = \alpha^2 + 1,\ \alpha^9 = \alpha^3 + \alpha,\ \alpha^{10} = \alpha^2 + \alpha + 1,\ \alpha^{11} = \alpha^3 + \alpha^2 + \alpha,\\
\alpha^{12} = \alpha^3 + \alpha^2 + \alpha + 1,\ \alpha^{13} = \alpha^3 + \alpha^2 + 1,\ \alpha^{14} = \alpha^3 + 1,\ \alpha^{15}=1.
以上のようにすべての元を$\ \alpha^0, \alpha^1, \alpha^2, \alpha^3\ $によって表すことができます.$\alpha^3, \alpha^2, \alpha^1, \alpha^0\ $の係数をビットに見立てると,
\alpha^0 \leftrightarrow 1,\ \alpha^1\leftrightarrow 2,\ \alpha^2\leftrightarrow 4,\ \alpha^3\leftrightarrow 8,\
\alpha^4 \leftrightarrow 3,\ \alpha^5\leftrightarrow 6,\\ \alpha^6\leftrightarrow 12,\ \alpha^7\leftrightarrow 11,\
\alpha^8 \leftrightarrow 5,\ \alpha^9\leftrightarrow 10,\ \alpha^{10}\leftrightarrow 7,\\
\alpha^{11}\leftrightarrow 14,\ \alpha^{12} \leftrightarrow 15, \alpha^{13}\leftrightarrow 13,\ \alpha^{14}\leftrightarrow 9,\ \alpha^{15}\leftrightarrow 1.
$\textbf{a}\ $で成り立つ演算方法を確立することができれば,有限体$\ \mathbb{F}_{2^4}\ $を実現することができます.
拡大体を実装する
拡大体としてガロア体$\ GF(2^4)\ $を採用します.
ガロア体 GF(16) の元とインデックス
ガロア体$\ GF(2^4)\ $の元の集まり$\ \textbf{a}=(a_i)\ $とインデックス表$\ \textbf{b}=(b_i)\ $をつくります.
\textbf{a}= \{ 1, 2, 4, 8, 3, 6 , 12, 11, 5, 10, 7, 14, 15, 13, 9, 1\},\\
\textbf{b}= \{0, 0, 1, 4, 2, 8, 5, 10, 3, 14, 9, 7, 6, 13, 11, 12 \}.
$b_0=0\ $が気になるところですが,別に$\ 0\ $でも$\ 100\ $でもいいのですが,とにかく$\ a_0 = 1,\ b_1 = 0\ $のように対応してくれればいいんです.つまり,便宜上の$\ b_0=0\ $です.気にする必要ありません.
# -*- coding: utf-8 -*-
def galois2(k, l):
p = pow(2, k)
a = [1]
for i in range(p - 1):
a.append(a[i] * 2)
if a[i + 1] >= p:
a[i + 1] = a[i + 1] - p
a[i + 1] = a[i + 1] ^ l
return a
def table2(a, k):
b = []
for i in range(2 ** k):
b.append(0)
for i in range(1, 2 ** k):
for j in range(2 ** k - 1):
if a[j] == i:
b[i] = j
return b
if __name__ == "__main__":
# x^4 = x + 1 -> [0, 0, 1, 1] -> ll = 3
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
ガロア体 GF(16) の上の演算の実装
たし算
a_i + a_j := a_i \oplus a_j.
ひき算
a_i - a_j := a_i \oplus a_j.
かけ算
a_i\times a_j:=a_{b_{a_i}+b_{a_j}} = a_{i + j\pmod{2^4-1}}.
わり算
a_i / a_j:=a_{b_{a_i}-b_{a_j}} = a_{i - j\pmod{2^4-1}}.
べき乗算
a_i^n := a_{b_{a_i} \cdot n} = a_{i \cdot n\pmod{2^4-1}}.
特別に実装すべき演算は,かけ算とわり算,そしてべき乗算です.
# -*- coding: utf-8 -*-
from galfield import galois2, table2
def gtimes2(k, a, b, s, t):
return a[(b[s] + b[t]) % (2 ** k - 1)]
def gdiv2(k, a, b, s, t):
return a[(b[s] - b[t]) % (2 ** k - 1)]
def gpow2(k, a, b, s, l):
return a[(b[s] * l) % (2 ** k - 1)]
if __name__ == "__main__":
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
# Example of caluc over galois field
# ADD & SUB
print a[2] ^ a[5]
# MUL & DIV
print gtimes2(k, a, b, a[2], a[5])
print gdiv2(k, a, b, a[2], a[5])
# POW
print gpow2(k, a, b, a[2], 3)
[付録] 拡大体上でElGamal暗号を実装
ElGamal暗号(エルガマル暗号)は,1984年にエジプトのTaher Elgamal氏が提案した公開鍵暗号です.(安全でないので,たぶん実用されていないと思いますが...)本稿でElGamal暗号を実装することに特別な意味はありませんが,せっかくガロア体を実装したので,これを何かに応用したいと考えたため付録としてここに書き留めます.
ElGamal暗号のアルゴリズムは次の通りです.(一般的に公開鍵暗号のアルゴリズムは,鍵生成,暗号化,そして復号の3つから成り立っています.)まず,ガロア体$\ GF(2^4)$の元の集合$\ \textbf{a}=(a_i)\ $とインデックス表$\ \textbf{b}=(b_i)\ $をつくります.
-
鍵生成アルゴリズム
- $x\overset{U}{\leftarrow}\{ 0, 1, \cdots, 2^4-2\}.$
- $h\leftarrow a_x.$
- $x\ $が秘密鍵,$h\ $が公開鍵.
-
暗号化アルゴリズム
- 平文$\ m\in \textbf{a}\ $を選択.
- 乱数$\ r\overset{U}{\leftarrow}\{ 0, 1, \cdots, 2^4-2\}\ $を生成.
- $c_0 \leftarrow a_r,\ c_1 \leftarrow m\cdot h^r\ $が暗号文.
-
復号アルゴリズム
- $c_1 / c_0^x\rightarrow m\ $によって復号.
# -*- coding: utf-8 -*-
from random import randint
from galfield import galois2, table2
from galois import gtimes2, gdiv2, gpow2
def GEGKeyGen(a, k):
sk = randint(0, 2 ** k - 2)
pk = a[sk]
return [sk, pk]
def GEGEnc(m, a, pk, k):
r = randint(0, 2 ** k - 2)
return [a[r], gtimes2(k, a, b, m, gpow2(k, a, b, pk, r))]
def GEGDec(c, a, k, sk):
return gdiv2(k, a, b, c[1], gpow2(k, a, b, c[0], sk))
if __name__ == "__main__":
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
m = a[2]
key = GEGKeyGen(a, k)
sk = key[0]
pk = key[1]
cipher = GEGEnc(m, a, pk, k)
print m == GEGDec(cipher, a, k, sk)
その他の拡大体を実装するには...
既約多項式を見つければいいと思います.例えば,共通鍵暗号のAESでは$\ GF(2^8)\ $が使われますが,その既約多項式は$\ x^8 + x^4 + x^3 + x^2 + 1\ $です.また,galois2()の 排他的論理和で用いるビットは$[0, 0, 0, 1, 1, 1, 0, 1]$なのでgalfield.pyにおいてk = 8, ll = 29と設定すれば$\ GF(2^8)\ $を表現することができます.ここまで理解することができたならば,その他の拡大体も自力で実装できると思います.