AtCoder Beginner Contest 161 の各問題の考察を書いていきます。結果はD完でした。
A - ABC Swap
問題概要: 3つの箱 A, B, C があり、それぞれの箱には整数 X, Y, Z が入っている。箱 A, B の中身を入れ替え、その後、箱 A, C の中身を入れ替えた。それぞれの箱に入っている整数を求めよ。
A: 考察
各状態における箱の中身は以下の通りです。
| 状態 | 箱の中身 |
|---|---|
| 初期状態 | X, Y, Z |
| A, B の中身を入れ替えた後 | Y, X, Z |
| A, C の中身を入れ替えた後 | Z, X, Y |
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11500166
B - Popular Vote
問題概要: N 種類の商品があり、i 番目の商品の得票数は A(i) である。この中から M 個の商品を選びたい。ただし、得票数が総得票数の 1/(4M) 未満である商品は選べない。選ぶことが可能か否か判定せよ。
制約: M≤N≤100, A(i)≤1000
B: 考察
言われた通りに書く系の問題です。
総得票数を計算し、各商品の得票数が総得票数の 1/(4M) 以上であるか判定し、条件を満たす商品の個数を数えて、M 以上だったら可能です。
条件式 A(i) >= S / (4 * M) を A(i) * 4 * M >= S に変形すれば、整数の計算で完結できます。浮動小数点数で計算しても普通に通るようです。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11498609
C - Replacing Integer
問題概要: 整数 N, K が与えられる。x=N から始めて、x を |x - K| に置き換える操作を好きな回数だけ行う。x の最小値を求めよ。
C: 考察
例えば N=31, K=4 のとき、操作を行うと x は 31, 27, 23, 19, 15, 11, 7, 3, 1, ... (3, 1 の繰り返し) となります。
引き算の繰り返しは割り算なので、N を K で割ることを考えます。
N = q・K + r (0 ≤ r < K) となる整数 q, r が存在します。操作回数が q に近いときの x を観察すると以下のようになります:
- 操作回数が q 未満のとき x≥K
- 操作を q 回行うと x = r
- 操作を q+1 回行うと x = |r - K| = K - r
- 操作を q+2 回行うと x = |(K - r) - K| = r
したがって、x の最小値は min(r, K - r) (ただし r = N % K) です。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11494059
D - Lunlun Number
問題概要: ルンルン数を以下のように定義するとき、K 番目に小さいルンルン数を求めよ。
定義: 正の整数 X を10進表記したとき、隣り合う2桁の数字の差の絶対値がすべて1以下なら、X はルンルン数。(ただし、10進表記では先頭に 0 をつけないものとする。)
制約: K≤10^5
D: 考察
整数の除算を x//y と書きます。
K が小さいので、小さい方から K 個のルンルン数をすべて求められれば OK です。
1~9 はルンルン数です。10以上のルンルン数の性質を考えます。X が10以上のルンルン数なら、1桁目を削った X//10 もルンルン数です。(例えば 11234 → 1123 など)
逆にいうと、すべての10以上のルンルン数は 10X + d (X: ルンルン数、1≤d≤9) の形でかけます。また、1桁目の数字 d が取りうる範囲も X の1桁目 (X % 10) プラスマイナス 1 の3通りです。そのため、特定の X に対して 10X + d の形でかけるルンルン数を全列挙できます。
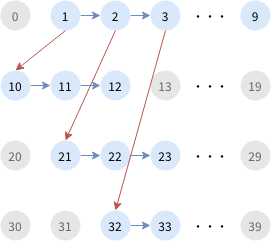
したがって、幅優先探索(BFS)で X → 10X + d と遷移していくことで、もれなく、だぶりなく、小さい順に、ルンルン数の列挙が可能です。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11521324
E - Yutori
問題概要: 整数 N, K, C と文字列 S が与えられる。1日目からN日目のうち、次の条件をすべて満たすようにK日を選んで働く。必ず働くことになる日を求めよ。
条件:
- i 日目に働くなら、i+1 日目から i+C 日目までは働かない。
- S(i) =
xなら i 日目には働かない。
制約:
- N≤10^5, 1≤K≤N, 0≤C≤N
- 働く日をK日以上選べる。
E: 考察
「i 日目は必ず働くことになる」は、言い換えると「i 日目に働かないとき、働く日数は K 未満」です。いったん「i 日目に働かないとき」の部分は忘れて、働く日数を最大にする方法を考えます。
日数 C に関する条件があるため、なるべく後続の C 日間に含まれる働ける日 (S(i)≠x の日) が少なくなるように、働く日を選ぶべきです。最後の働ける日は常に働く方がよい です。同時に、その直前の C 日間は働かないことが決定します。
C=2
v 最後の働ける日なので働く
oooxxooox
^^ ここで働いてしまうと最終日に働けないので、ここは働かない
働くか否かが決定した日は S(i)=x に変えて考慮から外してよいです。後は同様に、後ろから貪欲に働く日を決定できます。
v 働く日
oooxxxxxx
^ この日も働くことが確定
さて、i を固定して「i 日目は働かない」ことに決めたとします。上記の貪欲で i 日目が働く日に選ばれていない場合、i 日目に働かなくても問題なく K 日以上働けているので、i 日目は必ず働く日とはいえません。
一方、上記の貪欲で i 日目が働く日に選ばれていたとします。C の条件から、i+1 日目から i+C 日目は働く日に選ばれていません。そこで、次の2つを考えます。
- 1 日目から i-1 日目までに働く日数の最大値
- i+1 日目から N 日目までに働く日数の最大値
上記の貪欲から、後者の期間については「i+1 日目から i+C 日目まで働かない」ように、働く日を最大化できます。そのため、前者の期間から働く日をどのように選んでも C の条件には違反しません。
2つの期間に関して、どちらも上述の「後ろからの貪欲」で最大値を求められます。実装的には次のような DP です。
左側の区間に関する DP:
left(i) : 1 日目から i 日目までに働く日数の最大値
left(0) = 0
left(i+1) = max:
left(i)
left(max(i-C, 0)) + 1 (S(i)≠`x`のときのみ)
右側の区間に関する DP:
right(i) : i+1 日目から N 日目までに働く日数の最大値
right(N) = 0
right(i) = max:
right(i+1)
right(min(i+C+1, N)) + 1 (S(i)≠`x` のときのみ)
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11569666
リストの1要素以外の和を取るには両側から累積和、というのはしばしば見られるパターンのようです。本番では C の条件を処理できなかったのが敗因でした。
F - Division or Subtraction
問題概要: 正の整数 N がある。K を 2 以上 N 以下の正の整数とする。x = N から始めて、x が K 未満になるまで次の操作を繰り返すとき、最終的に x = 1 になるような K の個数を求めよ。
操作: x が K で割り切れるなら x に x / K を代入し、そうでなければ x - K を代入する。
F: 考察
N≤10^12 なのでシミュレーションは TLE です。
具体例を観察していきます。
例えば N = 12, K = 3 とすると x = 12, 4, 1 と遷移するので、この K は条件を満たします。一方 K = 4 とすると x = 12, 3 となり NG です。
K = 11, 12 のケースは自明で、それぞれ1回の引き算・割り算で x = 1 になります。K = N-1 なら x = N-(N-1) = 1 になり、K = N なら x = N/N = 1 になるため、どの N に対しても K = N-1, N は条件を満たすことが分かります。
2回 の割り算で x = 1 になるケースもあります。K = √N が整数なら (例えば N=16, K=4)、x = N (= K^2), N/K (= K), N/K^2 (= 1) となります。同様に、K = N^(1/m) が整数なら x = K^m, K^(m-1), ..., K^2, K, 1 です。
操作を逆順にみていくと、「x = 1 に K を足したり掛けたりすることで、N に一致させられるかどうか?」という問題と捉えられるようにみえますが、これは同値な言い換えではありません。
NG なケースの一例として挙げた N = 12, K = 4 も「足したり掛けたりして N に一致させられる」という条件は満たしています。x = 1 → 4 → 8 → 12 となります。しかしこれは、x = 12 のとき、K = 4 で割り切れるから割り算をするはずなのに、引き算をしてしまっているので、不正な操作です。
引き算を使うのは x が K で割り切れないときだけですが、それなら x - K も K で割り切れません。そのため、引き算を1度使ったら、割り算を使うことは2度とないはずです。
正常な操作の逆順は、K を x に何度か足した後、何度か K を掛けるという順番です。足し算を q 回、掛け算を m 回やるとしたら、(1 + q・K)・K^m = q・K^(m+1) + K^m と表せます。これが N に一致するような (q, m) の組み合わせがあれば、K は条件を満たします。逆にそのような (q, m) がなければ、K は条件を満たしません。
f(q, m) = q・K^(m+1) + K^m とおきます。非負整数 q, m を列挙して、条件 f(q, m) = N を満たす K を列挙していく方針を考えます。
q, m の値によって f(q, m) の性質が異なるので、場合分けをします。(q = 0 または m = 0 のときは f(q, m) のオーダーが低いので、q, m の列挙中に TLE するおそれがあります。)
- m = 0 のとき N = f(q, 0) = q・K + 1 です。変形すると K = (N-1)/q なので、N-1 の約数を列挙することで、条件を満たす K を得られます。
- m = 1 かつ q = 0 のときは K = N です。
- m = 1 かつ q≥1 のときは N = q・K^2 + K なので、K^2≤N の範囲で K を列挙して q = (N-K)/K^2 とおけばよいです。
- m≥2 のときは N = q・K^(m+1) + K^m ≥ K^2 なので、K^2≤N の範囲で K を列挙して、さらに K^m≤N となる m を列挙して、q = (N-K^m)/K^(m+1) とおけばよいです。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc161/submissions/11719649
公式解説にあるとおり、1回以上割り算をする (m≥1 の) ケースでは K は N の約数に絞られるので、この時点で O(√N) 時間が確定します。場合分けはもっと単純にできたようです。