AtCoder Beginner Contest 160 の各問題の考察を書いていきます。
A - Coffee
問題概要: 英小文字からなる長さ 6 文字列 S が与えられる。「Sの3文字目と4文字目が等しく、かつ、5文字目と6文字目も等しい」か否かを判定せよ。
A: 考察
A にしては珍しく、言われたとおりに書くだけの問題です。
Rust では、文字列 (str や String 型) に対してインデックスでアクセスできない (S[i] のように書けない) ので注意。一度、文字からなるベクタ (Vec<char>) に変換するとよいです。英小文字は1バイトなので、S.as_bytes()[i] のようにバイト単位で扱うという手もあります。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11277469
B - Golden Coins
問題概要: 500円硬貨1枚につき1000点、5円硬貨1枚につき5点のスコアが得られる。X 円をいくつかの硬貨に適切に両替するとき、合計スコアの最大値を求めよ。(ただし、硬貨は500円、100円、50円、10円、5円、1円の6種類。)
B: 考察
整数の除算を x//y で表します。
500円硬貨の場合は1円あたり2点、5円硬貨の場合は1円あたり1点のスコアなので、可能なかぎり500円硬貨に両替した方がスコアが大きくなります。
いうまでもないことかもしれませんが、両替で得る500円硬貨の枚数は条件 X = 500a + r (a, r は非負整数) を満たす a の最大値なので、a = X//500 です。残金は (X - 500a) なので、5円硬貨の枚数は b = (X - 500a)//5 で求まります。1000a + 5b が答えです。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11275945
C - Traveling Salesman around Lake
問題概要: 一周 K メートルの円形の湖があり、その周りに N 軒の家がある。i 番目の家は、湖の北端から時計回りに A(i) メートルの位置にある。いずれかの家から出発して湖の周上を移動し、N 軒すべての家を訪れるとき、最短の移動距離を求めよ。
C: 考察
仮に1番目の家から出発して湖をほぼ一周し、N番目の家まで訪れるとすると、湖の円周のうち 通らなかった 部分はN番目の家と1番目の家の間 (北側) だけです。「どの家から出発するか」の代わりに「どの家の間を通らないか」を考えます。通らない2軒の家の間の距離を d とするとき、最短の移動距離は K-d になるので、d の最大値を求められれば OK です。
制約をみると A は昇順で与えられるので、1番目からN-1番目までの家の間は A(i+1) - A(i) です。(1≤i≤N-1)
N番目と1番目の家の間の距離は、1番目の家が北端から時計回りに A(1)+K の位置にあると考えれば、(A(1)+K)-A(N) で表せます。
そういうわけで家の間の距離を列挙できるので、最大値 d が求まり、最短距離 K-d が計算できます。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11272459
D - Line++
問題概要: 正の整数 N, X, Y が与えられる。無向グラフ G = (V, E) を次のように定義するとき、各 k (1≤k≤N-1) についてクエリ(k)に答えよ。
グラフ G の定義:
- 頂点集合 V = {1, 2, ..., N}
- 辺集合 E = {(i, i+1)|1≤i≤N-1}∪{(X, Y)}
クエリ(k): 最短距離が k に等しい頂点のペア (i, j) (ただし 1≤i < j≤N) の個数を求めよ。
制約: N≤10^3, X + 1 < Y
D: 考察
グラフ G は N 頂点のパスグラフに、頂点 X, Y 間に辺を1つ加えたものになっています。
O(N^2) が間に合うので、頂点間の最短距離を事前にすべて求めるのがよさそうです。頂点 u, v (u < v) の最短距離は、辺 (X, Y) を通るケースと通らないケースのどちらかなので、それらの短い方をとれば求まります。
- 辺 (X, Y) を通るケースでは、u→X→Y→v だから |u-X|+1+|Y-v| です。(X < Y なので、Y→X の方向で通ると遠回りになります。)
- 辺 (X, Y) を通らないケースでは、u→u+1→...→v-1→v のようにパスグラフの上を直進するのが最短なので、距離は (v-u) です。
最短距離 dist(u, v) = k がすべて求まったら、k について分類して (u, v) の個数を数えておけば、各クエリは O(1) 時間で答えられます。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11295359
E - Red and Green Apples
問題概要: A 個の赤色のリンゴがあり、i 番目のおいしさは p(i) である。同様に、B 個の緑色のリンゴがあり、おいしさは q(i) である。C 個の無色のリンゴがあり、おいしさは q(i) である。無色のリンゴは着色して、赤色または緑色のリンゴとみなしてもよい。これらのリンゴのうち、赤色のリンゴの X 個、緑色のリンゴを Y 個食べる。食べるリンゴのおいしさの合計の最大値を求めよ。
制約:
- X≤A
- Y≤B
- A, B, C≤10^5
E: 考察
無色のリンゴがないケースを考えてみると、赤・緑のリンゴをそれぞれおいしさ順にソートして、上位の X, Y 個を食べればよいです。
上位のおいしさを持つ赤・緑のリンゴよりもおいしさの大きい、無色のリンゴがあるなら、それは食べた方がいいです。代わりに、食べる予定だったリンゴのうち、もっともおいしさの小さいものを食べないことにすると、結果を最大化できます。この処理は、食べる予定の赤・緑のリンゴを優先度付きキューに入れておけば、高速に実現できます。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11297972
公式の editorial に書いてありますが、おいしさが上位でない (赤・緑それぞれの上位 X, Y 個に入らない) リンゴは絶対に食べないので、無視してよいです。すると、残りのリンゴをどう選んでも、赤色のリンゴを X 個以下、緑色のリンゴを Y 個以下、無色のリンゴを 0 個以上、食べることになります。無色のリンゴを適当に着色すれば必ず条件を満たせます。したがって、リンゴの色を区別する必要はもはやなく、残りのリンゴをおいしさ順にソートして上位 X+Y 個を食べれば OK です。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11366051
F - Distributing Integers
問題概要: N 個の頂点からなるラベルつき木がある。各 k (k = 1, ..., N) について、クエリ(k)に答えよ。
クエリ(k): 以下の手順に従って木の各頂点に整数 1, ..., N を書くとき、整数の書き方の個数を求めよ。(mod 10^9+7)
手順:
- 頂点 k に 1 を書く。
- すでに整数が書かれた頂点に隣接している、まだ整数が書かれていない頂点を1つ選び、次の整数を書く。
制約: N≤10^5
F: 考察
はじめに「各頂点 k について木DPする」解法を考えます。頂点 k を決めて、木を根つき木とみなします。
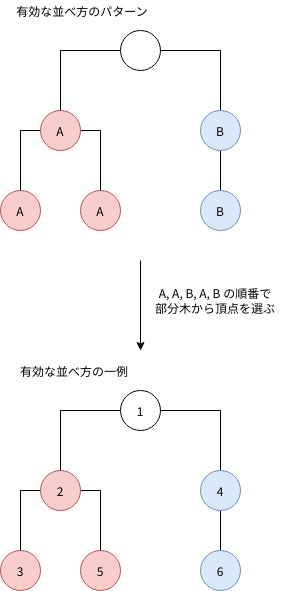
クエリ(k)の整数を書いていく工程は、頂点を一列に並べる ことと言い換えられます。整数の書き方に対応する並べ方を「有効な並べ方」と呼ぶことにします。(形式的には有効な並べ方 P を、すべての n について P(..n) に含まれる頂点に制限した誘導部分グラフが根 k を含む木であること、と定義できると思います。)
根を除く頂点の並べ方は、「各頂点が属する部分木」と「部分木内の頂点の並べ方」に分解できます。(形式的には「頂点の並べ方が有効であることと、各部分木に含まれる頂点に制限した部分列がすべて有効であることが同値である」ことを使うと示せると思います。)
「各頂点が属する部分木」の並べ方の個数は重複順列の場合の数です。「部分木内の頂点の並べ方」は再帰的に求まります。クエリ(k)の解を dp(k) で表し、頂点 u を根とする部分木に含まれる頂点の個数を size(u) で表して、漸化式を立てます。
\begin{align}
\operatorname{dp}(u)
& = \frac{(\sum_v{\operatorname{size}(v)})!}{\Pi_v \operatorname{size}(v)!} \cdot \prod_v \operatorname{dp}(v) \\
& = \frac{(\operatorname{size}(u) - 1)!}{\Pi_v \operatorname{size}(v)!} \cdot \prod_v \operatorname{dp}(v) \\
& = (\operatorname{size}(u) - 1)! \cdot \prod_v \frac{\operatorname{dp}(v)}{\operatorname{size}(v)!}
\end{align}
(v は頂点 u の直接の子である各頂点。)
上述の通りに実装すると、全体で O(N^2) 時間かかるので TLE します。そこで使うのが 全方位木DP です。
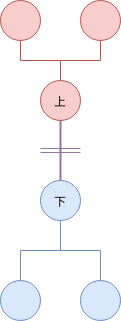
とりあえず根がないと考えにくいので、適当に選んだ頂点 (例えば頂点 1) を根として、根つき木とみなします。また、頂点 u と親 p を結ぶ辺の両側にある部分木のうち、p を根とする側を「上」の部分木と呼び、u を根とする側を「下」の部分木と呼ぶことにします。
上述の解法は、同じ部分木に対する木DPを何度も行っていて無駄です。メモ化しても、総乗の計算に O(N) 時間かかるので、依然として全体で O(N^2) 時間かかってしまいます。
部分木ごとに計算結果を持つ だけでなく、累積和を使って総乗の部分の計算を O(1) にする ことにより、全体で O(N) 時間まで計算量を落とします。
頂点 u の i 番目の辺を uv とするとき、uv の部分木に関するクエリの解を dp(u, i) で持ち、部分木のサイズを size(u, i) で持ちます。
はじめに通常の木DPを行い、各頂点の下の部分木に対する dp(u, i) を求めます。
次にもう一度、根からDFSを行います。今度は上の部分木に対する dp(u, i) を求めたいです。再帰的に頂点を訪問するとき、訪問済みの各頂点の上の部分木に関する dp(u, i) がすべて求まっているようにします。
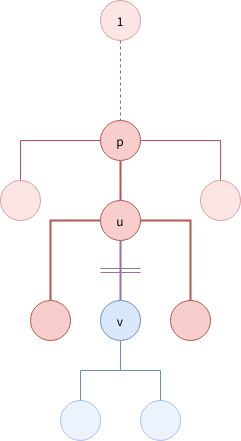
頂点 u を訪れた段階で、すべての i について dp(u, i) が求まっています (上の図の赤い辺)。これらを使って、総乗の部分の計算のための累積和を用意します。左からの累積和と右からの累積和を使うと、「ちょうど1つの辺を除いて総乗の部分を計算する」ことが O(1) 時間で可能になります。
頂点 u から子 v に入る際に、頂点 v の上の部分木に関する dp(v, j) を求めます。頂点 v の上の部分木の子要素は、v の兄弟 (u の v 以外 の子) と、u の親 (あれば) です。そのため、v を除く総乗の部分を累積和により計算すれば、dp(v, j) が O(1) 時間で求まります。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc160/submissions/11443211
size(u, i) も全方位木DPで求めています。(上の部分木のサイズは下の部分木のサイズを N から引いて求めてもいいです。)
参考: 木と計算量 後編 〜全方位木DP〜 (「予習」の部分のコードを大いに参考にしています)