大学の授業で巡回セールスマン問題を解く課題があったので、Haskellでこの問題を解いてみました!
そもそも巡回セールスマン問題とは?
複数の都市があって、セールスマンはその場所を一回ずつ通ります。最短経路で全ての場所を通って戻ってくるにはどのルートを通ればいいですか、という問題です。
まずデータ構造を定義する
入力データ(場所の情報)は、x座標とy座標です。例えば、1つ目の場所は座標(90, 100)にあります。
90 100
40 15
30 30
座標の型を定義する (Coord)
座標が出てきたので、これを型にしてしまいましょう。
newtype Coord = Coord (Double, Double) deriving (Eq)
2点間の距離、例えば(90, 100)、(40, 15)の距離を図りたいときは、ユークリッド距離を使います。
Haskellでかくとこのような感じ。
distance :: Coord -> Coord -> Double
distance (Coord (x1, y1)) (Coord (x2, y2)) = sqrt $ (x1 - x2)^2 + (y1 - y2)^2
巡回路を定義する (Path)
また、座標を複数格納できるPath型も定義しましょう。
import Data.Vector
newtype Path = Vector Coord
ここではリストではなく、Vectorを使うことにします。
また、PathとPathを比較できるように、Ord型クラスのインスタンスにしましょう。
instance Ord Path where
compare p1 p2
| totalCost p1 > totalCost p2 = GT
| totalCost p1 == totalCost p2 = EQ
| totalCost p1 < totalCost p2 = LT
合計の距離の計算をどうするか?
例えば、3地点を(90,100), (40,15), (30,30)という順番で通るとします。そのときの移動距離は、
(90,100)と(40,15)の距離 + (40,15)と(30,30)の距離 + (30,30)と(90,100)の距離
となります。そこで、totalCostという関数を作ります。
eachTuple :: Vector Coord -> Vector (Coord, Coord)
eachTuple path =
let tuples = do
index <- enumFromTo 0 (length path - 2)
return (path ! index, path ! (index + 1))
in tuples `snoc` (last path, head path)
totalCost :: Path -> Double
totalCost (Path path) = sum $ uncurry distance <$> eachTuple path
eachTupleで、2点間の座標をタプルにしています。つまり、[ ((90,100), (40,15)), ((40,15), (30,30)), ((30,30), (90,100)) ]のようになります。それをdistanceにそれぞれ適用させて、あとはそれらを合計しています。
あとは、これらをTSP.hsにまとめてしまいましょう。(TSPは、traveling salesman problemの略です。)
module TSP (
totalCost
, Path(..)
, Coord
) where
import Data.Vector
import Prelude hiding (
enumFromTo,
length,
last,
head,
sum
)
newtype Coord = Coord (Double, Double) deriving (Eq, Show, Ord)
newtype Path = Path (Vector Coord) deriving (Eq, Show)
instance Ord Path where
compare p1 p2
| totalCost p1 > totalCost p2 = GT
| totalCost p1 == totalCost p2 = EQ
| totalCost p1 < totalCost p2 = LT
eachTuple :: Vector Coord -> Vector (Coord, Coord)
eachTuple path =
let tuples = do
index <- enumFromTo 0 (length path - 2)
return (path ! index, path ! (index + 1))
in tuples `snoc` (last path, head path)
totalCost :: Path -> Double
totalCost (Path path) = sum $ uncurry distance <$> eachTuple path
distance :: Coord -> Coord -> Double
distance (Coord (x1, y1)) (Coord (x2, y2)) = sqrt $ (x1 - x2)^2 + (y1 - y2)^2
どのアルゴリズムで解くの?
今回は遺伝的アルゴリズムで解きます!
遺伝的アルゴリズム
簡単に言えば、生物がどのようにして進化したかをアルゴリズムにしたものです。詳しくは↓
遺伝的アルゴリズム
遺伝的アルゴリズムは、以下のアルゴリズムで構成されています。
- N個の個体(巡回路)をランダムに初期化
- 親を選んで交叉する (crossover)
- 低確率で突然変異 (mutation)
- 次の世代の個体(巡回路)を選択する (selection)
今回は、ランダムな要素も入っているので、それぞれの関数をIOにしました。遺伝的アルゴリズムの全体像はこんな感じです。
また、最良解を保存するために「エリート保存」をしています。
mating :: Vector Path -> IO (Vector Path)
mating = undefined
mutation :: Vector Path -> IO (Vector Path)
mutation = undefined
selectChildren :: Vector Path -> IO (Vector Path)
selectChildren = undefined
geneticLoop :: Int -> Vector Path -> Path -> IO Path
geneticLoop 0 _ elite = return elite
geneticLoop generation parents elite = do
newParents <- mating parents >>=
mutation >>=
selectChildren
let minPath = minimum newParents :: Path
newElite = min minPath elite :: Path
printf "%d generation , %f , %f\n" generation (totalCost newElite) (totalCost minPath)
geneticLoop (generation - 1) newParents newElite
1. N個の個体(巡回路)をランダムに初期化
ここでは、巡回路をシャッフルすることで初期化します。Vectorにはshuffle関数はないようなので、自分で実装しました。
型はこのような感じにしました。
shuffleM :: (Eq a) => Vector a -> IO (Vector a)
shuffleM x = undefined
ここでは、aがCoord型になります。
shuffleの実装は、ある要素を1つずつランダムにポップして、それらを連結するかんじです。
例えば以下のようにシャッフルします。
-
[0,1,2,3]をシャッフル - ランダムにインデックスを選ぶ(
1のインデックスが選ばれたとする) -
[0,1,2,3]から1をポップして、その1を結果に入れる。 - 新たに
[0,2,3]をシャッフルする
これらを繰り返します。
Shuffleモジュールを作ったので、それを載せておきます。
module Shuffle (
shufflePath,
shuffle,
shuffleM
) where
import TSP
import System.Random
import Data.Vector
import Prelude hiding (head, tail, length)
shufflePath :: Path -> StdGen -> Path
shufflePath (Path coords) gen = Path $ shuffle coords gen
shuffle :: (Eq a) => Vector a -> StdGen -> Vector a
shuffle x gen
| x == empty = empty
| otherwise =
let (index,newGen) = randomR (0, length x - 1) gen :: (Int, StdGen)
targetElm = x ! index
in targetElm `cons` shuffle (deleteFirst targetElm x) newGen
shuffleM :: (Eq a) => Vector a -> IO (Vector a)
shuffleM x = do
gen <- newStdGen
return $ shuffle x gen
-- | 削除したい要素の中で最初に出てきたものを取り除く
-- >>> deleteFirst 2 $ fromList [1..5]
-- [1,3,4,5]
-- >>> deleteFirst 1 $ fromList [1,2,3,4,1]
-- [2,3,4,1]
deleteFirst :: (Eq a) => a -> Vector a -> Vector a
deleteFirst x vector
| x == head vector = tail vector
| otherwise = head vector `cons` deleteFirst x (tail vector)
あとは、以下のようにして使いましょう。
import Shuffle (shuffleM)
import TSP
inputPath :: IO (Vector Coord)
inputPath = do
contents <- getContents
return $ fromList $ toCoord . words <$> lines contents
where
toCoord :: [String] -> Coord
toCoord [s1, s2] = Coord (read s1, read s2)
toCoord _ = error "it is illegal file format!"
main :: IO ()
main = do
coords <- inputPath
paths <- replicateM poolSize $ Path <$> shuffleM coords
2. 親を選んで交叉する
交叉とは、親の遺伝子が交わることを指します。人間も同じように親の遺伝子を受け継いでいますよね。
具体的には、以下のようにしました。
- 2つの巡回路(親)をランダムに選択
- 順序交叉(order crossover)
2つの巡回路(親)をランダムに選択
まず、複数の巡回路から2つの巡回路をランダムに選ぶ関数を作りましょう。
randomRSt :: (RandomGen g, Random a) => (a, a) -> State g a
randomRSt (a,b) = state $ randomR (a,b)
twoRandomNumState :: (Random a) => (a,a) -> State StdGen (a, a)
twoRandomNumState fromTo = do
n1 <- randomRSt fromTo
n2 <- randomRSt fromTo
return (n1, n2)
twoRandomNum :: (Random a) => (a,a) -> StdGen -> (a,a)
twoRandomNum fromTo = evalState (twoRandomNumState fromTo)
randomSelect :: Vector Path -> IO (Path, Path)
randomSelect paths = do
gen <- newStdGen
let n = length paths
(r1, r2) = twoRandomNum (0, n - 1) gen
return (paths ! r1, paths ! r2)
2つのランダムな数字を安全に生成するために(誤って同じ乱数ジェネレータを使わないように)、Stateモナドを使いました。twoRandomNum関数は、ある範囲の中で2つの乱数を作ります。
順序交叉(order crossover)
さきほど選んだ2つを交叉させます。順序交叉は以下のように交叉します。
- ランダムに交叉点を決める
- 子1は、親1から左側をそのまま受け継ぎ、親2からは「親1から引き継いだものを除いたもの」を受け継ぐ。
- 同様に、子2は、親2から左側をそのまま受け継ぎ、親2からは「親1から引き継いだものを除いたもの」を受け継ぐ。
といった感じです。
orderCrossOver :: Path -> Path -> IO (Vector Path)
orderCrossOver papa@(Path coords) mama = do
gen <- newStdGen
let n = length coords
(dividePoint,_) = randomR (1, n - 1) gen :: (Int, StdGen)
return $ divCpChromo dividePoint mama papa
divCpChromo :: Int -> Path -> Path -> Vector Path
divCpChromo divPoint (Path papa) (Path mama) =
let (p1, p2) = splitAt divPoint papa :: (Vector Coord, Vector Coord)
m1 = filter (`notElem` p1) mama :: Vector Coord
m2 = filter (`notElem` p2) mama :: Vector Coord
in Path (p1 ++ m1) `cons` singleton (Path (m2 ++ p2))
交叉点をインデックスの1からn-1としているのは、0からだと何も入れ替わらないからです。
あとは、今説明した処理を繰り返せばいいだけです。
mating :: Vector Path -> IO (Vector Path)
mating parents = do
childList2 <- replicateM (length parents) $ do
(papa, mama) <- matingSelection parents
crossOver papa mama :: IO (Vector Path)
return $ concatVector childList2
concatVector :: Vector (Vector a) -> Vector a
concatVector = concatMap id
これでmating関数ができあがりました。
3. 低確率で突然変異
今回は10%の確率で、巡回路がシャッフルされます。Vectorの要素を1つずつ確認するような処理なので、foldlを使ってみました。
mutationRate = 0.1
mutation :: Vector Path -> IO (Vector Path)
mutation children = do
gen <- newStdGen
return $ fst $ foldl mutate (empty, gen) children
where
mutate :: (Vector Path, StdGen) -> Path -> (Vector Path, StdGen)
mutate (ps, gen) p = do
let (r, newG) = randomR (0, 1) gen :: (Double, StdGen)
if r < mutationRate
then (shufflePath p newG `cons` ps, newG)
else (p `cons` ps, newG)
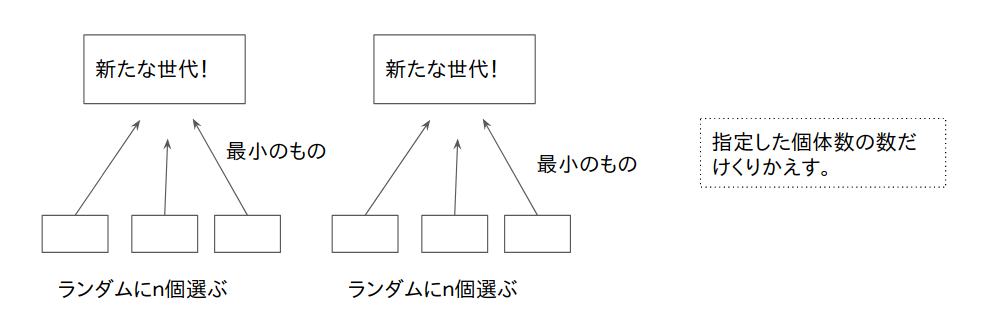
4. 次の世代の個体(巡回路)を選択する (selection)
今回は、トーナメント選択を使います。
- ランダムにn個選ぶ
- その中からcostが最小のものを選ぶ
- 指定した分だけ繰り返す
まず、複数の巡回路から1つの巡回路をランダムに選択する関数を作りましょう。
randomSelectOne :: Vector Path -> IO Path
randomSelectOne paths = do
gen <- newStdGen
let n = length paths
(index, _) = randomR (0, n - 1) gen :: (Int, StdGen)
return $ paths ! index
そして、トーナメント選択をする関数を作ります。
tournamentSelect :: Int -> Int -> Vector Path -> IO (Vector Path)
tournamentSelect poolSize n paths = replicateM poolSize $ do
randomSelectPath <- replicateM n (randomSelectOne paths)
return $ minimum randomSelectPath
ここでのnは、トーナメントの大きさです。上の図ではn=3になっています。
poolSizeは、「指定した分だけ繰り返す」ものです。
全体のコード
あとは、main関数でgeneticLoop関数を呼べばいいですね。
generationNum = 100
main = do
coords <- inputPath
paths <- replicateM poolSize $ Path <$> shuffleM coords
elite <- geneticLoop generationNum paths (head paths)
print $ totalCost elite
Githubに全体のコードを載せました。
Genetic-Algorithm-Haskell
実験
TSP Data for the Traveling Salesperson Problemからデータを取りました。att48.tspというデータセットを使います。
レポジトリをダウンロードして、以下のコマンドで実行できます。
$ stack build
$ stack exec genetic-algorithm-vector < input/48node.txt
結果があまりよくない場合は、poolSizeの値を増やしましょう。
なお、最適解は33523.70850743559だと思われます。
結果
generationNum = 100、poolSize=6000で試しました。
100 generation 117502.3637 117502.3637
99 generation 111547.6981 111547.6981
98 generation 98044.69584 98044.69584
97 generation 95280.17597 95280.17597
96 generation 95280.17597 100666.9047
95 generation 95280.17597 101406.8389
94 generation 95280.17597 100290.5332
.
.
.
7 generation 34714.01486 34714.01486
6 generation 34714.01486 34714.01486
5 generation 34714.01486 34714.01486
4 generation 34714.01486 34714.01486
3 generation 34714.01486 34714.01486
2 generation 34714.01486 34714.01486
1 generation 34714.01486 34714.01486
34714.014857028
100.689914082s
研究室のマシンで試したので、実行速度はかなり速いです。
グラフにしてみると、こんな感じです。
最適解が33523.70850743559なので、100秒で34714.014857028出せるのは優秀ですね。
実は遺伝的アルゴリズムのライブラリがHaskellにある
mooというライブラリがあるようですね。
あとがき
がんばりました。
Haskellで遺伝的アルゴリズムを実装するのは大変かなと思いましたが、案外かけました。Haskellは型がしっかりしているし、とてもプログラムが設計しやすく、かきやすい言語だなと感じました。
Haskellでいろいろ考えながらコーディングするのが楽しかったです。おわり。