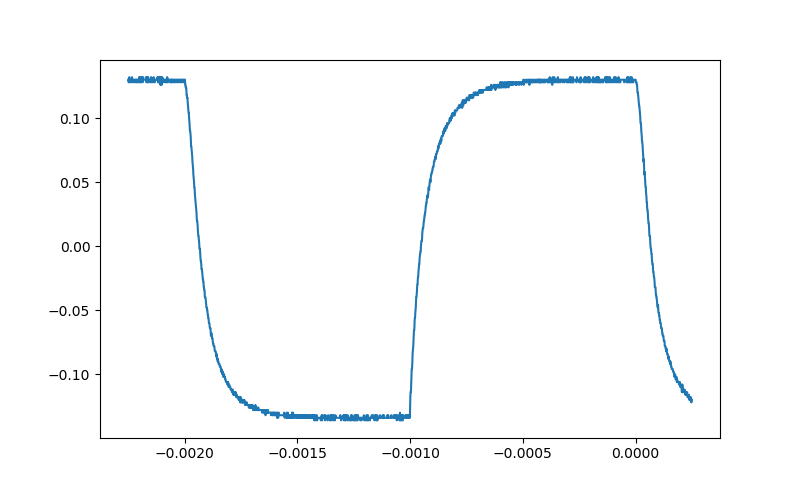
対象とするグラフ
こんな感じの応答プロファイルをフィッティングしたい。今までは普通に
ae^{-\frac{t-t_0}{\tau}}+c \\
a(1-e^{-\frac{t-t_0}{\tau}})+c
を使ってフィッテイング範囲と$t_0$、$t_1$を目で確認しながらフィッティングしていたがとてもメンドくさいのでどうにかしてpythonで一発でフィッテイングできないか考えてみた。
フィッティング関数
色々調べてみたところ、pythonは数式内にxの条件を加えることができるらしい。どういうことかというと、
y = \begin{cases}
1 & (x >0) \\
0 & (x\leq0)
\end{cases}
のようなステップ関数を、pythonでは、
y = 1 * (x > 0)
と一発で記述することができるらしい。当初if文を使ってゴリゴリ場合分けすることを覚悟していたが、これで相当手間が省ける。
今回の場合は2つの応答プロファイル(0s以降は無視)が重なった形をしているため、それぞれのスタート時刻を$t_0$、$t_1$として3つに場合分けをする。すなわち、
y = \begin{cases}
a+c & (x \leq t_0) \\
ae^{-\frac{t-t_0}{\tau_0}}+c & ( t_1>x > t_0) \\
a(1-e^{\frac{t-t_1}{\tau_1}})+c & (x \geq t_1)
\end{cases}
となる。pythonで記述すると
a*(1*(x<=t0)+np.exp(-(x-t0)/b1)*(x>t0)*(x<=t1)+(1-np.exp(-(x-t1)/b2))*(x>t1))+c
となる。
それでは、この関数で適当に初期値を与えてフィッティングを試してみる。モジュールはscipyのcurvefitを使用する。
param_ini = (0.2, 0.0001, 0.0001, -0.1, -0.002, -0.001) #初期値
param_bound = ([0,0,0,-np.inf,-np.inf,-np.inf],[np.inf,10,10,np.inf,np.inf,np.inf]) #拘束条件
def response_func(x, a, b1, b2, c, t0, t1) :
return a*(1*(x<=t0)+np.exp(-(x-t0)/b1)*(x>t0)*(x<=t1)+(1-np.exp(-(x-t1)/b2))*(x>t1))+c
def normal_fit() :
try :
param, cov = curve_fit(response_func, fit_list_x, fit_list_y, p0 = param_ini, maxfev = 10000, bounds=param_bounds)
print(param)
except RuntimeError :
pass
ここでparam_iniは初期値で$(a,\tau_0,\tau_1,c,t_0,t_1)$のセットである。今回はグラフを目で見てそれぞれの初期値を入力した。結果のグラフがこちらだ。
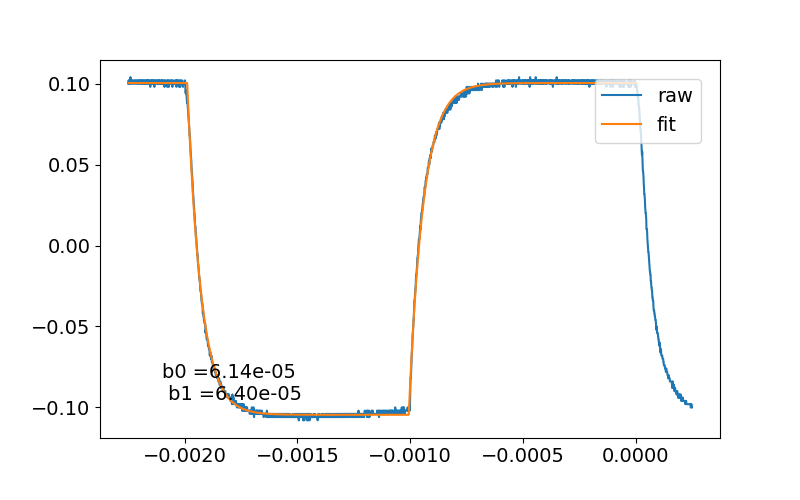
おお…うまくいってるようだ。しかし問題が発覚した。初期値の$t_0$、$t_1$を少し変えてしまうと全くフィッティングできなくなるのだ。例えば、$t_0=-0.003$、$t_1=-0.001$と設定するとこんなことになってしまう。
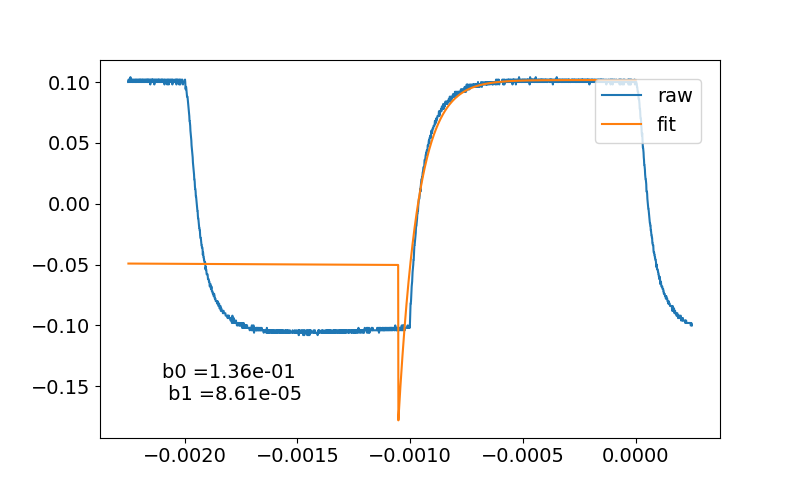
それに対し、他のパラメーター、$a$、$\tau_0$、$\tau_1$、$c$については正解から何倍かずれた値をいれてもフィッティングに問題は生じなかった。つまり、この方法ではフィッティングの可否が$t_0$、$t_1$の初期値に鋭敏であり、グラフを目でみて正解に近い$t_0$、$t_1$の初期値を逐一与えなければうまくいかないということだ。それではオール自動化の目的に反するので良くない。そこでこの初期値依存の問題を解決するために2つの方法を試してみた。
方法1:basin hopping法
ここのページの説明がわかりやすい。
Python SciPy : 大域的最適化アルゴリズム
要するに最初にランダムな初期値を作成し、それぞれで局所的最小値を得る。次にこれを比較して新たに初期値を設定しなおす、以下繰り返し・・・で大域的最小値に辿りつけるといったものである。
param_ini = np.array([0.2, 0.0001, 0.0001, -0.1, -0.002, -0.001]) #初期値
def response_func(x, a, b1, b2, c, t0, t1) :
return a*(1*(x<=t0)+np.exp(-(x-t0)/b1)*(x>t0)*(x<=t1)+(1-np.exp(-(x-t1)/b2))*(x>t1))+c
# basin hopping method
def randomstep_fit() :
param_ini2 = np.array(param_ini)
def calc_cost(param, x, y) :
return ((y - response_func(x, *param))**2).sum()
minimizer_kwargs = {"args":(np.array(fit_list_x), np.array(fit_list_y))}
try :
result = basinhopping(calc_cost, param_ini, stepsize=1.,minimizer_kwargs=minimizer_kwargs)
print(result.x)
except RuntimeWarning or RuntimeError :
pass
しかし、この方法でも、多少改善するもののまだ初期値によってはフィッティングの失敗が起こる。結局真の$t_0$、$t_1$に近い初期値を入力してやらないとダメそうだ。
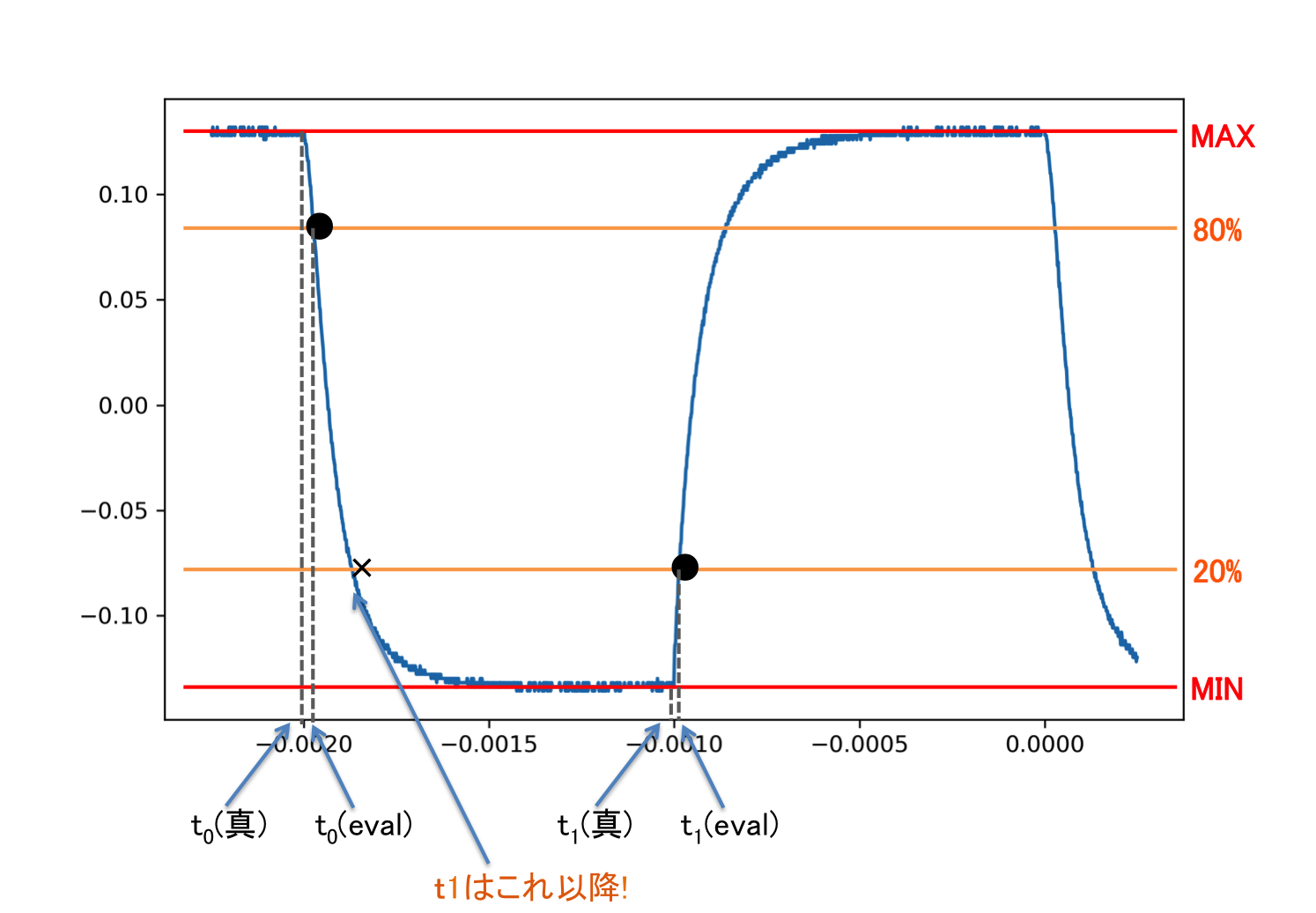
方法2: t0、t1の見積もり
yの最大値と最小値を求めて、その差の20%,80%の値をスレッショルドとして利用する。初期の傾きが急峻なexpならではのやり方。つまり、$t_0$の初期値は80%値を下回る直前でかつyの傾きが負であるxで規定する。$t_1$は図中に書かれているバッテン以降で、20%を超える直前でかつyの傾きが正であるxで規定する。
# データの立ち上がり点と立ち下がり点を見積もって初期値のリストを返す
def evaluation_updown(y) :
l = 0
m = 0
ymax =max(y)
ymin =min(y)
threshold0 = (ymax-ymin)*down_th + ymin
threshold1 = (ymax-ymin)*up_th + ymin
while fit_list_y[l] > threshold0 :
if sum(fit_list_y[l-3:l])-sum(fit_list_y[l:l+3]) < 0 :
l += 1
continue
l += 1
m = l
while fit_list_y[m] > threshold1 :
if sum(fit_list_y[m-3:m])-sum(fit_list_y[m:m+3]) < 0 :
m += 1
continue
m += 1
while fit_list_y[m] < threshold1 :
if sum(fit_list_y[m-3:m])-sum(fit_list_y[m:m+3]) > 0 :
m += 1
continue
m += 1
return [ymax, ini_tau_down, ini_tau_up, ymin, fit_list_x[l],fit_list_x[m]]
この関数ではついでに最大値と最小値をそれぞれ$a$、$c$の初期値として初期値のリストparam_iniを返してくれる。傾きの正負を判定するあたりのコードにその場しのぎ感が滲み出ている。しかし、これで初期値を設定し、フィッティングを行ったところ、basinhoppingを使わずとも成功率が爆上げした。
コード
import string
import codecs
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit, basinhopping
import numpy as np
import glob
import os
directory = "D:\\OneDrive\\test8" #ファイルのあるディレクトリ
basinhopping_flag = 0 #0の場合、curvefit、1の場合はbasinhoppingでfittingする。
fit_range = [-0.00225,-0.00000] #フィッティングしたいxの範囲
x_fit_min = -0.00225 #xのフィッティング範囲の下限
x_fit_max = -0.00000 #xのフィッティング範囲の上限
down_th = 0.8 #データの立ち下がり点を見積もるためのスレッショルド
up_th = 0.2 #データの立ち上がり点を見積もるためのスレッショルド
### 初期値設定###
ini_tau_down = 0.0001 #立ち下がりの時定数初期値
ini_tau_up = 0.0001 #立ち上がりの時定数初期値
###############
# fit_rangeの下限と上限に相当するインデックスをxのデータ系列から取得する。
def range_limiter(x,lower,upper) :
i = 0
j = 0
dt = x[1] - x[0]
if dt > 0 :
while x[i] <= lower :
i += 1
while x[j] <= upper :
j += 1
return [i,j]
else :
while x[-i] <= lower :
i += 1
while x[-j] <= upper :
j += 1
return [-j,-i]
# データの立ち上がり点と立ち下がり点を見積もって初期値のリストを返す
def evaluation_updown(y) :
l = 0
m = 0
ymax =max(y)
ymin =min(y)
threshold0 = (ymax-ymin)*down_th + ymin
threshold1 = (ymax-ymin)*up_th + ymin
while fit_list_y[l] > threshold0 :
if sum(fit_list_y[l-3:l])-sum(fit_list_y[l:l+3]) < 0 :
l += 1
continue
l += 1
m = l
while fit_list_y[m] > threshold1 :
if sum(fit_list_y[m-3:m])-sum(fit_list_y[m:m+3]) < 0 :
m += 1
continue
m += 1
while fit_list_y[m] < threshold1 :
if sum(fit_list_y[m-3:m])-sum(fit_list_y[m:m+3]) > 0 :
m += 1
continue
m += 1
return [ymax, ini_tau_down, ini_tau_up, ymin, fit_list_x[l],fit_list_x[m]]
# フィッティング関数
def response_func(x, a, b1, b2, c, t0, t1) :
return a*(1*(x<=t0)+np.exp(-(x-t0)/b1)*(x>t0)*(x<=t1)+(1-np.exp(-(x-t1)/b2))*(x>t1))+c
# 通常のフィッティング
def normal_fit() :
try :
param, cov = curve_fit(response_func, fit_list_x, fit_list_y, p0 = param_ini, maxfev = 10000, bounds=param_bounds)
print(param)
ax1.plot(fit_list_x, response_func(fit_list_x, *param),"-",label = "fit")
ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=1)
ax1.text(0.1,0.1,f"b0 ={'%.2e' %param[1]} \n b1 ={'%.2e' %param[2]}",transform=ax1.transAxes)
except RuntimeError :
pass
# basin hopping method
def randomstep_fit() :
param_ini2 = np.array(param_ini)
def calc_cost(param, x, y) :
return ((y - response_func(x, *param))**2).sum()
minimizer_kwargs = {"args":(np.array(fit_list_x), np.array(fit_list_y))}
try :
result = basinhopping(calc_cost, param_ini2, stepsize=1.,minimizer_kwargs=minimizer_kwargs)
print(result.x)
except RuntimeWarning or RuntimeError :
pass
ax1.plot(fit_list_x, response_func(fit_list_x, *result.x),"-",label = "fit")
ax1.text(0.1,0.1,f"b0 ={'%.2e' %result.x[1]} \n b1 = {'%.2e' %result.x[2]}",transform=ax1.transAxes)
ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=1)
# Main
os.chdir(directory)
file_list = sorted(glob.glob("*.txt")) #拡張子が.txtであるファイルのリストを取得しソートする。
file_num = len(file_list)
for i in range(file_num) :
file = file_list[i]
file_name, ext = os.path.splitext(file)
list = []
list_x =[]
list_y = []
with codecs.open(file, "r", "utf-8", "ignore") as fileobj : #ファイルの中身をfileobjとして読み出す
for line in fileobj :
if string.digits.find(line[0]) == -1 and line[0] != "-": #ファイルのヘッダ情報(測定器情報とか測定日時とか書いてあるやつ)を無視するおまじない
continue
pre_list = line.strip().split() #一行の内容をスペースとかタブで区切ってlistにしてくれるスグレモノ
list_x.append(float(pre_list[0]))
list_y.append(float(pre_list[1]))
plt.rcParams["font.size"] = 14
fig = plt.figure(figsize=(8,5))
ax1 = fig.add_subplot(1,1,1)
ax1.plot(list_x, list_y, "-", label="raw")
fit_lower_idx, fit_upper_idx = range_limiter(list_x,*fit_range)
fit_list_x = list_x[fit_lower_idx : fit_upper_idx]
fit_list_y = list_y[fit_lower_idx : fit_upper_idx]
param_ini = evaluation_updown(fit_list_y)
param_bounds=([0,0,0,-np.inf,-np.inf,-np.inf],[np.inf,10,10,np.inf,np.inf,np.inf]) #拘束条件(第一項が下限、第二項が上限)
if basinhopping_flag == 0 :
normal_fit()
else :
randomstep_fit()
plt.savefig(f"{file_name}.png",dpi=100)
plt.close()
結果のグラフは
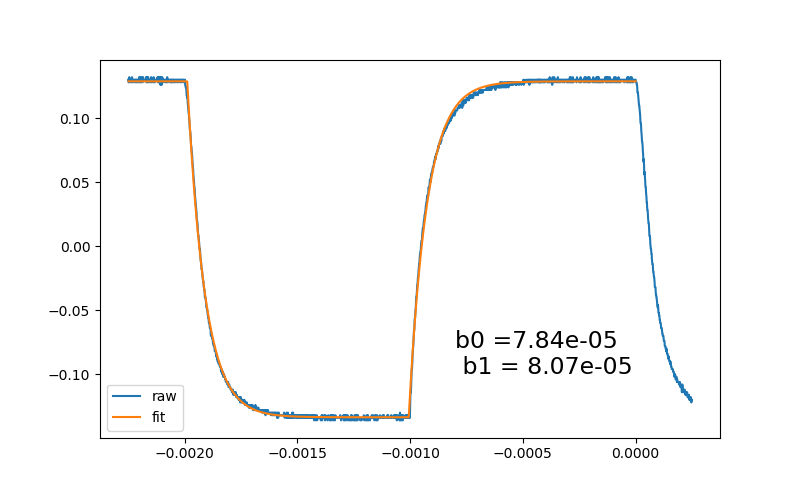
となりうまくフィッテイングできてることがわかる。やったね。
ちなみにこのコードで複数のデータを処理すると、curvefitよりbasin hoppingのほうがフィッテイング失敗率が高くなる。処理も遅いしいいことないので基本はbasin hoppingは使わなくてよいだろう。
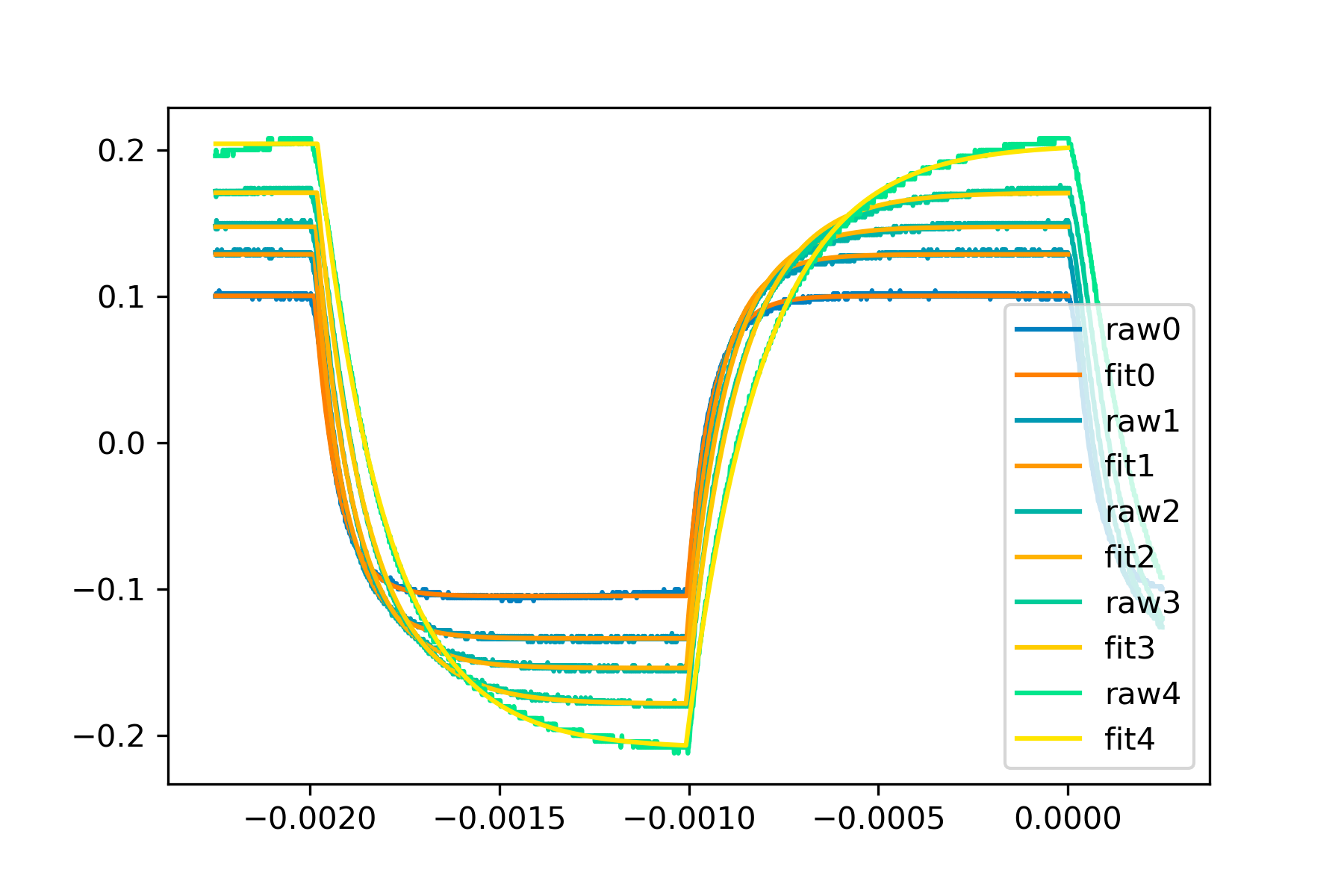
応答速度違うものをいっぱいフィッティングしても一桁くらいなら追従する。