対象としている手持ちのデータが、どのような特徴をもっているかを理解しておくことは、統計解析をおこなう際にとても重要。本当は、データを集める前に理解しておいたほうがいいのだろうけど、どこからともなくやってきたデータと向き合わなくてはいけない場合もあるし、そういうときに心得ておくと良いこと。そんなメモ。
多くの統計的検定の手法は、データが正規分布に従うことを仮定している。いわゆるパラメトリック手法といわれるやつ(母集団の分布型に一定の仮定をおく... 正規分布でなくてもおk?)がそれだ。
データが正規分布に従うかどうか(正規性)を確認する方法は、大きく分けて2つある。度数分布図(ヒストグラム)や正規確率グラフを用いて視覚的に確認するか、統計的手法を用いて客観的な評価をおこなうかである。もちろんRではどちらの方法も実行できるのでやってみる。
# 使用するパッケージの読み込み(作図用)
library(ggplot2)
library(gridExtra)
模擬データの生成
正規分布に従うデータと他の確率分布を使って生成したデータで比較する。Rに用意されている確率分布については、次のページに要約されている -> http://cse.naro.affrc.go.jp/takezawa/r-tips/r/60.html 。今回は、正規分布のほかに連続確率分布である連続一様分布、ガンマ分布およびベータ分布のデータを比較として用意する。
set.seed(100) # 乱数の固定
df.normal <- data.frame(x = rnorm(n = 200, mean = 0, sd = 1)) # 正規分布(平均0、分散1)に従うランダムなデータ
df.uniform <- data.frame(x = runif(n = 200, min = 0, max = 1)) # 一様分布に従うランダムな200個の観測値データ
df.gamma <- data.frame(x = rgamma(n = 200, shape = 1, rate = 1)) # ガンマ分布
df.beta <- data.frame(x = rbeta(n = 200, shape1 = 2, shape2 = 5)) # ベータ分布
分布型の確認
それぞれの確率分布関数の分布型を確認。
# 作図用の関数作成
gg_prob_dens <- . %>% {
ggplot(., aes(x)) + geom_density(colour = "#9BD3EE", fill = "#D0F3FF70")
}
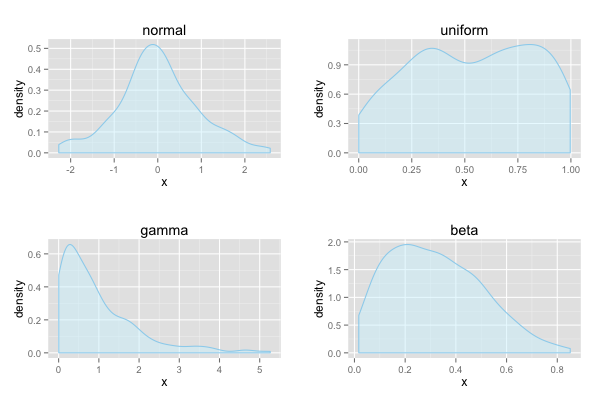
gg_prob_dens(df.normal) + ggtitle("normal") -> p1
gg_prob_dens(df.uniform) + ggtitle("uniform") -> p2
gg_prob_dens(df.gamma) + ggtitle("gamma") -> p3
gg_prob_dens(df.beta) + ggtitle("beta") -> p4
grid.arrange(p1, p2, p3, p4, ncol = 2)
正規分布からなるデータはほぼ左右対称な一峰型の分布となる。一様分布はほぼ平らな分布型。ガンマ分布およびベータ分布は右裾広がりの分布型をしている。
度数分布図(ヒストグラム)
# 作図用の関数を用意。ヒストグラムの幅は`nclass.Sturges`を使って適度に求める
gg_prob_hist <- . %>% {
ggplot(., aes(x)) + geom_histogram(binwidth = max(.$x) / nclass.Sturges(.$x))
}
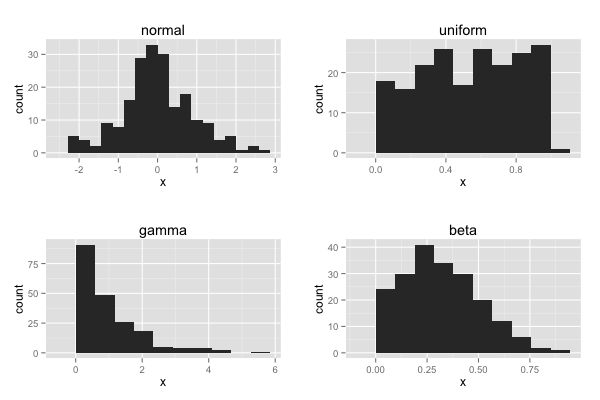
gg_prob_hist(df.normal) + ggtitle("normal") -> p1
gg_prob_hist(df.uniform) + ggtitle("uniform") -> p2
gg_prob_hist(df.gamma) + ggtitle("gamma") -> p3
gg_prob_hist(df.beta) + ggtitle("beta") -> p4
grid.arrange(p1, p2, p3, p4, ncol = 2)
正規分布以外の確率分布で生成したデータなので、一様分布、ガンマ分布、ベータ分布に従う各データは正規分布のような一峰型の左右対象な形をしていない。
正規確率グラフ
あまりこういう表現を見ないが...。視覚的に正規性を確かめる方法はヒストグラムの他に、正規確率グラフを描いてみる方法がある。これは度数分布図で得られた度数の累積値より作成される累積度数分布図の縦軸を変形したものであり、正規分布であればデータが直線上に並ぶものである。Rではqqnorm()やqqplot()が用意されている。
gg_prob_qq <- . %>% {
ggplot(., aes(sample = x)) +
stat_qq()
}
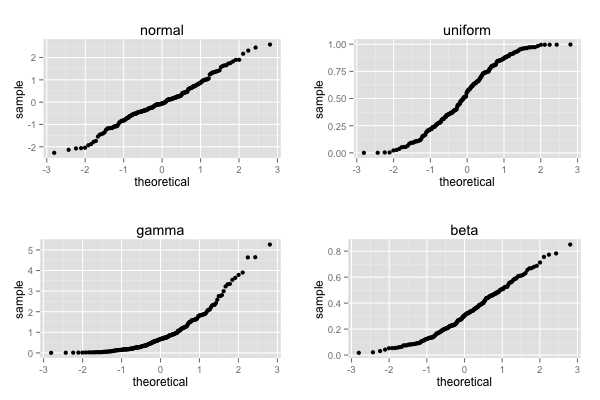
gg_prob_qq(df.normal) + ggtitle("normal") -> p1
gg_prob_qq(df.uniform) + ggtitle("uniform") -> p2
gg_prob_qq(df.gamma) + ggtitle("gamma") -> p3
gg_prob_qq(df.beta) + ggtitle("beta") -> p4
grid.arrange(p1, p2, p3, p4, ncol = 2)
正規分布のデータに対して、ガンマ分布のデータは明らかに直線の形をしていない。しかし、他の分布型のデータはなんとなく直線っぽい。データによってはこの方法はよくないのかもしれない。
シャピロ-ウィルクの正規性の検定
次からは統計的手法による客観的評価方法である。シャピロ-ウィルクの正規性の検定は単刀直入に、データが正規分布に従うかどうかを確かめる。
帰無仮説は「標本は正規母集団からサンプリングされたものである」となる。
shapiro.test(df.normal$x)
# Shapiro-Wilk normality test
#
# data: df.normal$x
# W = 0.9884, p-value = 0.102
結果はP値が0.12となり、帰無仮説を棄却するものではなかった。各データの検定結果は次のようになる。
| 確率分布 | P値 | 帰無仮説の棄却(P < 0.05) |
|---|---|---|
| 正規分布 | 0.1020452 | No |
| 一様分布 | 0.0000048 | Yes |
| ガンマ分布 | 0.00000000000001501 | Yes |
| ベータ分布 | 0.000172 | Yes |
正規分布以外の確率分布で生成した模擬データに対しては、どれも正規分布に従うものではないということがわかった。
コルモゴロフ-スミルノフ検定
コルモゴロフ-スミルノフ検定(言いにくいし、覚えにくい...)は2つの母集団の確率分布が異なるかどうかを調べるために用いられる。データの分布型の位置と形が考慮されるため、比較対象に正規分布からなるデータを指定すれば、手持ちのデータが正規分布と等しいか異なるかがわかる。
**帰無仮説は「二つの分布が等しい」**である。Rではks.test()で実行する。
ks.test(df.normal, "pnorm", alternative = "two.sided")
# One-sample Kolmogorov-Smirnov test
#
# data: df.normal
# D = 0.0734, p-value = 0.2318
# alternative hypothesis: two-sided
正規分布に従う模擬データでは、P値が0.05よりも大きく、帰無仮説を棄却することはできない、という結果、すなわち、正規分布に従うデータである、という結果が得られた(当然なのだけど)。他の確率分布データに対しても実行した結果をまとめると以下のとおり。
| 確率分布 | P値 | 帰無仮説の棄却(P < 0.05) |
|---|---|---|
| 正規分布 | 0.2318105 | No |
| 一様分布 | 2.2e-16 | Yes |
| ガンマ分布 | 2.2e-16 | Yes |
| ベータ分布 | 2.2e-16 | Yes |
中心極限定理
脇道にそれて。Qiitaにも最近記事が書かれていたので便乗してみる(参考リンクを参照)。
今回扱っている確率分布からなる模擬データは、中心極限定理によってその標本平均はサンプルサイズを大きくすると正規分布に近似するようになる。せっかくなのでこうしたデータが上記の正規性の確認方法に対し、どういう挙動をとるのかを検証してみる。
# 模擬データを用意
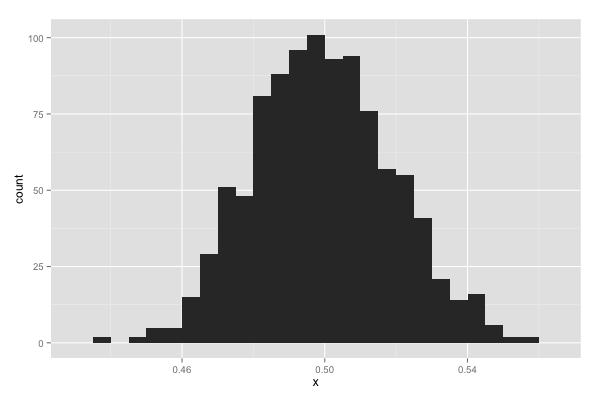
df.dummy.normal <- data.frame(x = sapply(seq(1000), function(x) { mean(runif(200)) }))
ggplot(df.dummy.normal, aes(x)) + geom_histogram(binwidth = 0.005)
元は一様分布であるが、その標本平均からなる多量のデータは正規分布のような形になった。
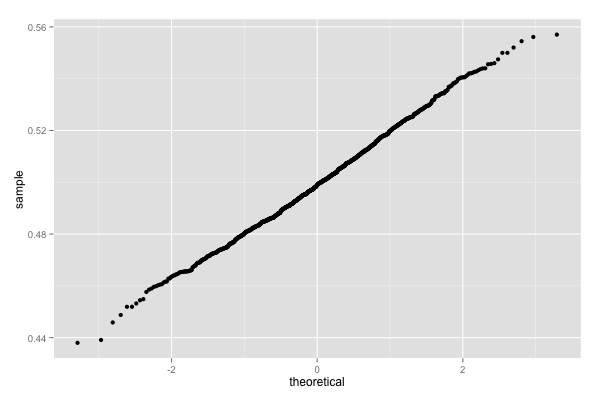
gg_prob_qq(df.dummy.normal)
ほぼ直線である。
shapiro.test(df.dummy.normal$x)$p.value # 0.04125348
ks.test(df.dummy.normal$x, "pnorm")$p.value # 2.2e-16
どちらの検定方法でも帰無仮説は棄却され、正規分布に従わないという結論となった。
まとめ
そこまで厳しく言われることは少ないのかもしれない(査読者次第...)が、データが正規分布に従うか、そうでないか(どの確率分布に従うか)を理解しておくことは解析の段階で大事である。現実のデータでも、ヒストグラムや正規確率グラフを描いてみて、どのような形をしているか確認すると、正規分布なのかそうでない分布型をしているのかがわかることがあるので、解析を始める前に図を描いてみるべし。また、より客観的な評価を行うためには統計的手法に検定を用いるべし。
参考
- Sokal, R. R. & Rohlf, F. J. 藤井宏一訳 (1983). 生物統計学. 共立出版
- 市原 清志 (1990). バイオサイエンスの統計学. 南江堂
- Nicholas J. Gotelli & Aaron M. Ellison (2012). A Primer of Ecological Statistics 2nd Ed. Sinauer
- Rでt検定 1
- R-Source
- 05distributionR.html
- Rを使った統計勉強法【中心極限定理編】 - Seeking for my unique color.
- statistics - 【統計学】中心極限定理のイメージをグラフで掴む - Qiita
- 可視化で理解する中心極限定理 #rstatsj - Qiita
- RPubs - Central Limit Theorem on R