Algorithm | 二分木（binary tree）をPython3で解説

二分木とは

二分木とは、2つに分かれていく木構造のこと。

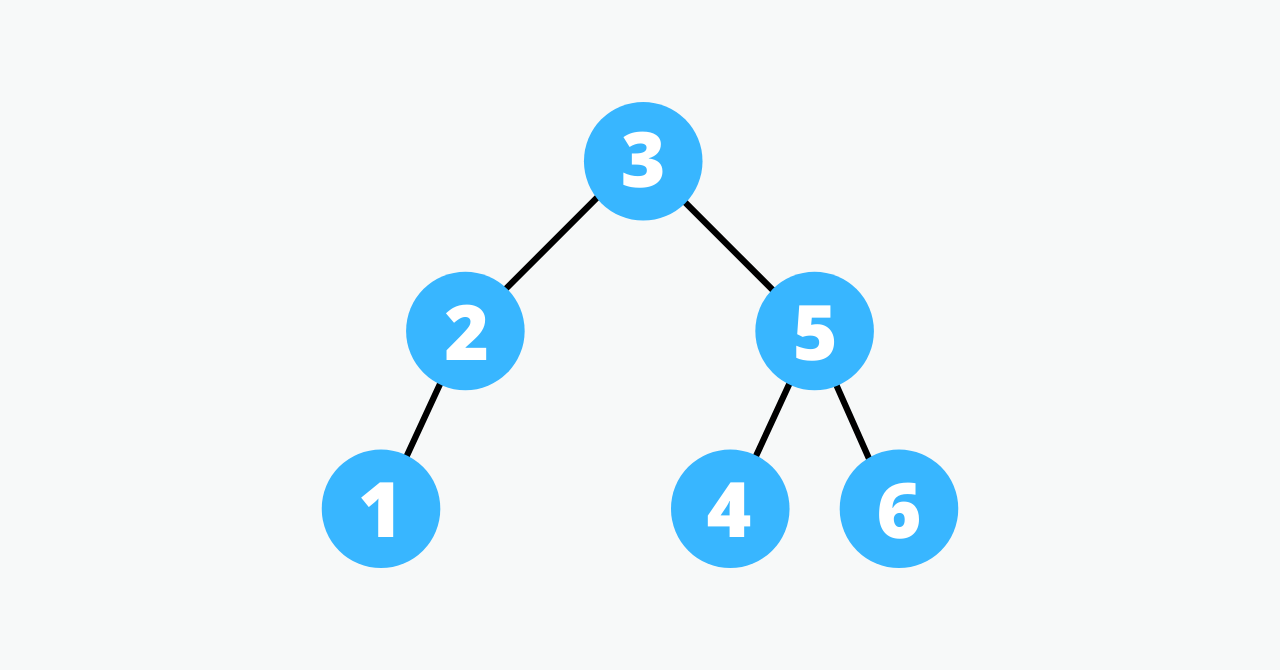
例えば、次のような構造である。

3から2と5のnodeが出ている。

このように1つのnodeから2つ以上の枝が出ないような木構造のことを二分木という。

nodeと枝の作成

nodeまたは、それをつなげる枝を作成するためには、class Node:というものを定義する必要がある。これがないと、node同士をつなぐことができない。

class Node(object):
    def __init__(self, label):
        self.label = label
        self.left = None
        self.right = None

二分木の作成

二分木を作成するためには、再帰を用いて、次のようなコードで実装できる。

def insert(node, label):
    if node == None:
        return Node(label)
    
    if label < node.label:
        node.left = insert(node.left, label)
    else:
        node.right = insert(node.right, label)
    return node

上図のような二分木にしたいときは、次のように書いてあげると良い。

if __name__ == '__main__':
    root = None
    root = insert(root, 3)
    root = insert(root, 2)
    root = insert(root, 5)
    root = insert(root, 1)
    root = insert(root, 4)
    root = insert(root, 6)
    print(root.label)
    print(root.right.label)
    print(root.left.label)
    print(root.right.left.label)
    print(root.left.left.label)

output
>> 3
>> 5
>> 2
>> 4
>> 1

それぞれの出力から、場所があっていることがわかる。

また、次のように書いても、同じような出力が得られる。

if __name__ == '__main__':
    root = Node(3)
    root.left = Node(2)
    root.right = Node(5)
    root.left.left = Node(1)
    root.right.left = Node(4)
    root.right.right = Node(6)
    print(root.label)
    print(root.right.label)
    print(root.left.label)
    print(root.right.left.label)
    print(root.left.left.label)

output
>> 3
>> 5
>> 2
>> 4
>> 1

木のなぞり

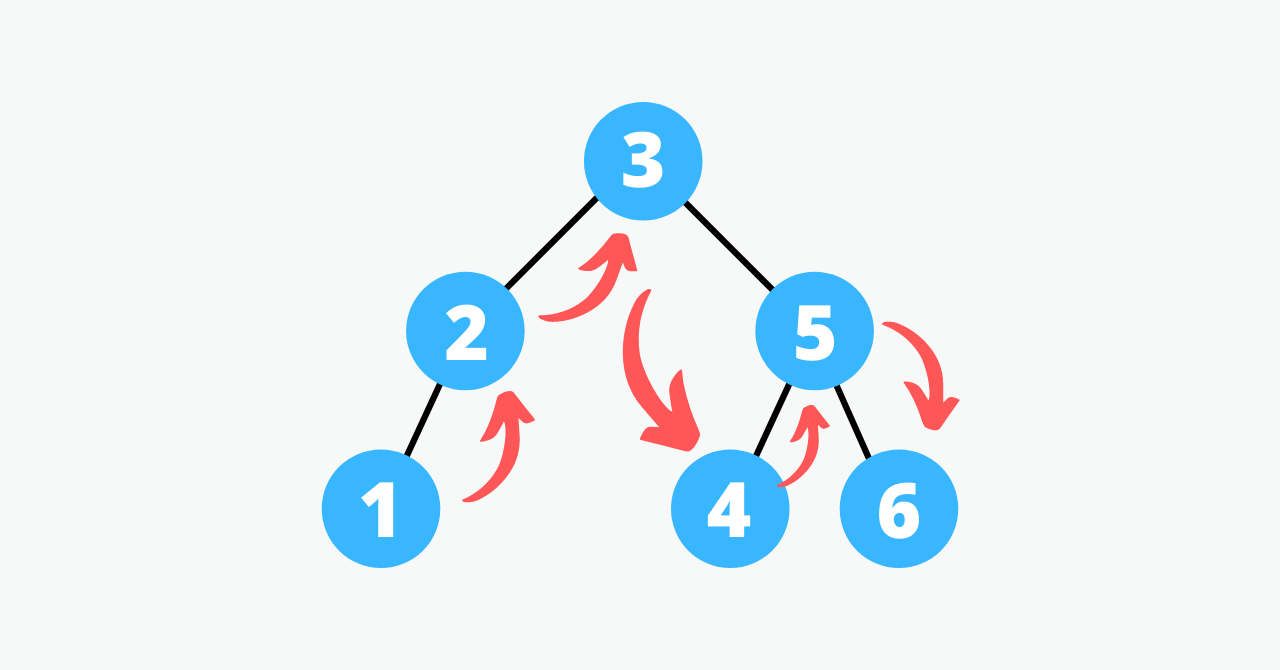
二分木のなぞりかたには、大きく分けて3種類ある。inorderとpreorderとpostorderである。

それぞれのコードは以下のように書ける。

inorder

# inorder
def inorder(node):
    if node != None:
        inorder(node.left)
        print(node.label)
        inorder(node.right)

if __name__ == '__main__':
    root = None
    root = insert(root, 3)
    root = insert(root, 2)
    root = insert(root, 5)
    root = insert(root, 1)
    root = insert(root, 4)
    root = insert(root, 6)
    inorder(root)

output
>> 1
>> 2
>> 3
>> 4
>> 5
>> 6

inorderは、left->label->rightの順番になぞるものである。3種類のなかでは最もポピュラーで、よく使われている。

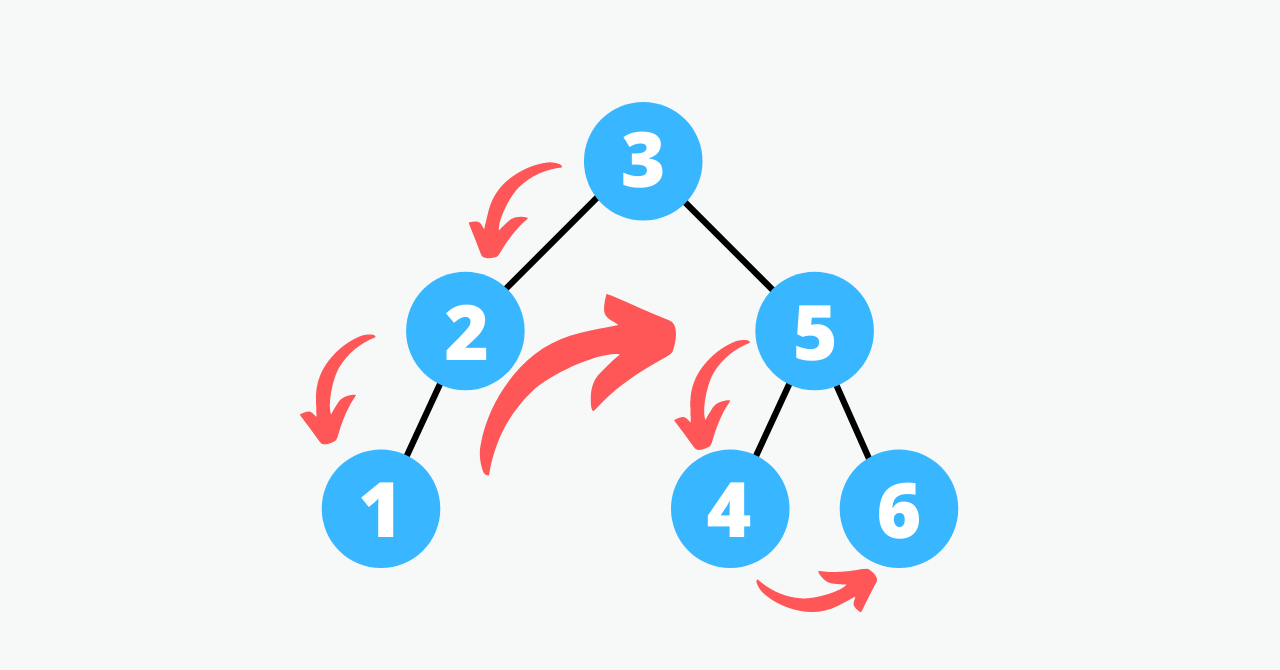
preorder

# preorder
def preorder(node):
    if node != None:
        print(node.label)
        preorder(node.left)
        preorder(node.right)

if __name__ == '__main__':
    root = None
    root = insert(root, 3)
    root = insert(root, 2)
    root = insert(root, 5)
    root = insert(root, 1)
    root = insert(root, 4)
    root = insert(root, 6)
    preorder(root)

output
>> 3
>> 2
>> 1
>> 5
>> 4
>> 6

preorderは、label->left->rightの順番になぞるものである。木の高層から左側から降りていくようなイメージである。

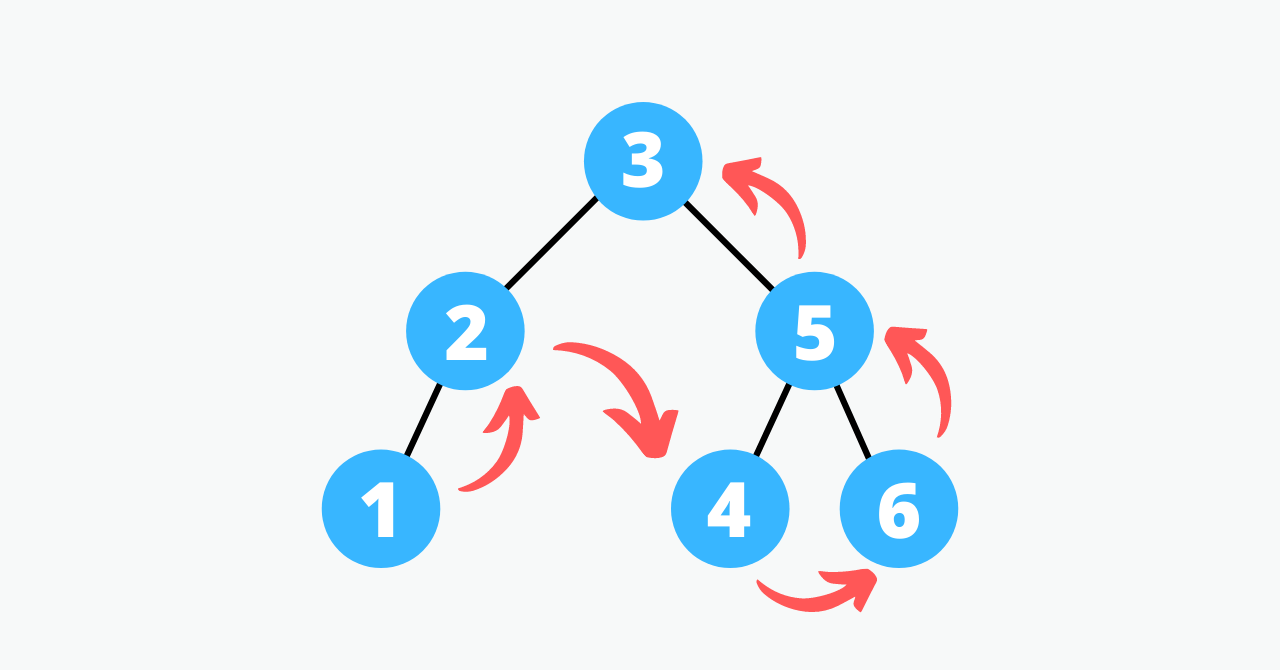
postorder

# postorder
def postorder(node):
    if node != None:
        postorder(node.left)
        postorder(node.right)
        print(node.label)

if __name__ == '__main__':
    root = None
    root = insert(root, 3)
    root = insert(root, 2)
    root = insert(root, 5)
    root = insert(root, 1)
    root = insert(root, 4)
    root = insert(root, 6)
    postorder(root)

output
>> 1
>> 2
>> 4
>> 6
>> 5
>> 3

postorderは、left->right->labelの順番になぞるものである。preorderに比べると、低層から高層にかけてなぞっていくものである。

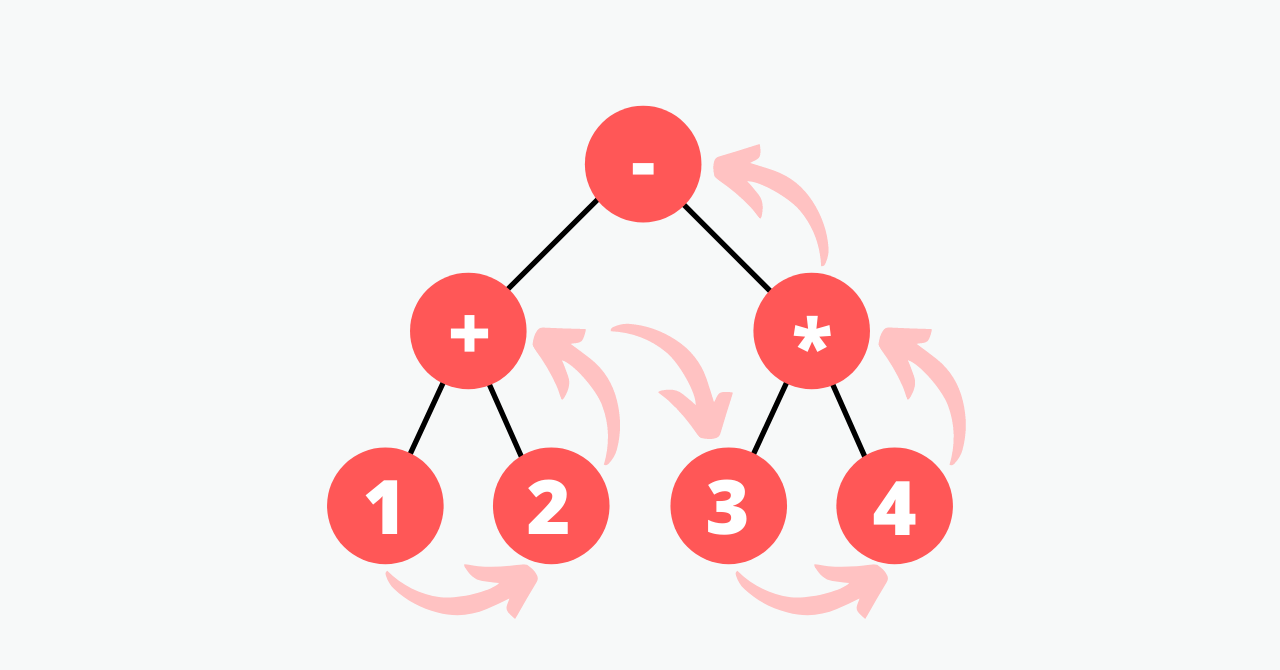
postorderを用いた逆ポーランド記法

また、postorderは、工夫すると逆ポーランド記法を出力することができる。

# rpn
def rpn(node):
    stack = []
    
    def _rpn(node):
        if node is not None:
            _rpn(node.left)
            _rpn(node.right)
            stack.append(node.label)

            return ' '.join(stack)
    
    return _rpn(node)

if __name__ == '__main__':
    root = Node('-')
    root.left = Node('+')
    root.right = Node('*')
    root.left.left = Node('1')
    root.left.right = Node('2')
    root.right.left = Node('3')
    root.right.right = Node('4')
    print(rpn(root))

output
>> 1 2 + 3 4 * -