keras でパターンを数える

#パターンの密度と計数
　ニューラルネットワークでは、パターンの 密度 の推定は難しいという記載がある。[1]
　一方、某社では、「ある駐車場で、モニターカメラ映像をもとにして満車率を算出している」という噂を聞いた。[3]
　満車率というのは、駐車場におけるクルマの密度に他ならないのではないか？

　　　　　　　　　_{画像 ©2018 Google}
　また一般に、密度というのは、「枠の中にある特定パターン数の比率」と、言い換えることができると思う。
　上記の駐車場の例では、モニター画像からクルマというパターンの数を数えることで満車率＝密度を算出してる、ということでは？

　というわけで、今回は、keras を用いて、ニューラルネットワークが「パターンの数を数える」ことのポテンシャルを探ってみる　ことにした。

　今回はポテンシャルを探る目的なので、実用性よりも、極力シンプルなパターンの数を数えること、を目標とする。
たとえば、次の左の画像には☆が 50 個あるので、この画像をモデルに放り込むと、50 という答えを出してほしい。

同様に、次の画像には☆が４個あるので、4 という答えを出してほしい。

と、ここで「これじゃダメじゃん！」と気づく。
以上のような画像データをモデルに学習させた場合、☆の数ではなく、「白い領域の面積の割合」を学習して、一見、正解らしい回答を出力してしまうかもしれない。

そこで、次のように大きさをマチマチにしても、☆が4個なら 4 という答えを出してもらいたい。是非とも！

　ここではあくまで、「パターンの数を数えて欲しい」ので、わざと大きさを変えて「数える」という概念を叩き込もうという、スパルタ教育をしようというわけである。
　ただ、☆ は２次元データとはいえ、ある程度は複雑なので、「パターンを数えるポテンシャルを探る」という目的から、さらに　究極的にシンプルなパターン　を考えてみることにしよう。
　すなわち、２次元よりシンプルなパターンを、１次元配列（要素数は 20 ）で表現する。ここでは、上述の☆の代わりに、'1' がひとつ以上集まった島 をパターンと考え、その島の数を数えてもらう。

###ソースリスト：
https://github.com/uminor/counter
-> counter.py

##訓練データ例

入力データ	正解	意味
[0 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0]	2	'1'の島が 2 個
[1 1 1 1 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0]	3	'1'の島が 3 個
[0 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 1 0 0 1]	4	'1'の島が 4 個
[1 1 1 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 1 0]	5	'1'の島が 5 個
： 　　　:	：	：

今回は、このような正解データ 500 個をランダムに生成し、モデルに学習させる。

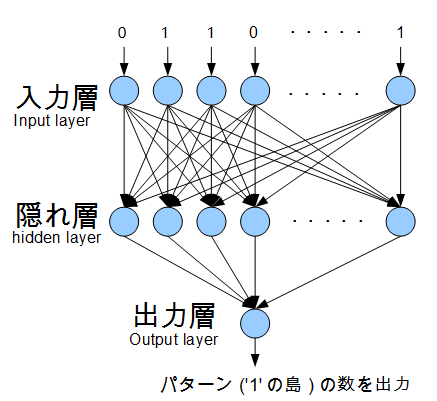
###モデルの形状

レイヤー	ユニット数	活性化関数
入力層	20
隠れ層(１層)	20	sigmoid
出力層	1	linear
一種の 回帰モデル といえるかな。

モデル部分のソース（説明用に修正）

model.add(Dense(units = 20, input_dim = 20, use_bias = bias))
model.add(Activation('sigmoid'))
model.add(Dense(units = 1, use_bias = bias))
model.add(Activation('linear'))
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss = 'mean_squared_error', optimizer = sgd)

##学習
学習回数（エポック）は、100000回。
1000回程度でも、それなりに近い答えが出されるが、さらに回数を重ねると徐々に精度が向上（誤差率が減少）した。

model.fit(i_train, o_train, epochs = 100000, verbose = 1)
　　i_train:入力データ, 　o_train：正解データ

##検証用データと予測結果
学習済みモデルに、100個の検証用データを与え、島の数を数えてもらうと、実数で答え（予測値）を得た。
o_predict = model.predict(i_test)
　　i_test:検証用データ, 　o_predict ：予測データ

予測値に関して、四捨五入すれば、98%正解 となるレベルとなった。
(不正解は下記*の２件：すなわち誤差が0.5以上)

検証用データ	予測	正解	差異
[1 1 1 1 0 0 0 1 1 1 1 0 0 0 0 1 0 0 1 0]	3.44	4	-0.56
[0 1 1 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1]	2.83	3	-0.17
[1 1 1 1 1 1 0 0 0 1 0 0 0 1 1 1 1 1 1 1]	2.96	3	-0.04
[1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1]	3.32	3	0.32
[1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0]	1.98	2	-0.02
[0 1 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1]	3.03	3	0.03
[0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 0]	4.53	5	-0.47
[0 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 0 1 0]	3.73	4	-0.27
[0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1]	1.93	2	-0.07
[1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0]	3.45	3	0.45
[1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1 0 0 0]	2.79	3	-0.21
[1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 1 0 0]	3.01	3	0.01
[1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0]	3.06	3	0.06
[1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 1 1 0]	2.99	3	-0.01
[0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1]	1.98	2	-0.02
[0 0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 1]	2.97	3	-0.03
[0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1]	1.95	2	-0.05
[1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 1 1]	2.94	3	-0.06
[1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0]	1.88	2	-0.12
[0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 1 1]	2.18	2	0.18
[1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0]	1.88	2	-0.12
[1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0]	2.02	2	0.02
[1 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0]	*3.72	3	0.72
[1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 1]	3.20	3	0.20
[0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0]	2.01	2	0.01
[0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0]	0.95	1	-0.05
[0 1 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 1 1 1]	3.02	3	0.02
[0 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 0 0]	2.94	3	-0.06
[0 0 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0]	1.98	2	-0.02
[0 1 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 0 0 0]	2.65	3	-0.35
[1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 0 0]	3.04	3	0.04
[0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 0 0 0]	2.33	2	0.33
[0 0 0 1 0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 0]	3.02	3	0.02
[1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 0 1 1 0]	3.18	3	0.18
[0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1]	3.05	3	0.05
[1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 0 0 0]	*3.50	3	0.50
[0 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 0 0 0]	1.99	2	-0.01
[0 0 0 0 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 1]	3.19	3	0.19
[1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0]	2.86	3	-0.14
[1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1]	5.11	5	0.11
[0 0 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0]	1.71	2	-0.29
[0 1 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0]	2.95	3	-0.05
[1 1 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0]	5.45	5	0.45
[0 0 1 1 1 0 0 0 0 0 1 1 0 0 1 1 1 1 1 1]	3.12	3	0.12
[1 0 0 0 1 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0]	3.76	4	-0.24
[0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1]	2.97	3	-0.03
[1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 0 0 1 1 0]	3.12	3	0.12
[1 0 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 1 1 1]	4.78	5	-0.22
[0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0]	1.96	2	-0.04
[0 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 0]	2.93	3	-0.07
[1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]	2.04	2	0.04
[1 0 0 0 1 0 0 0 1 1 0 0 1 1 0 0 0 0 0 1]	5.73	5	0.73
[1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1]	2.90	3	-0.10
[0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0]	1.93	2	-0.07
[1 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0]	4.14	4	0.14
[0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 1]	1.85	2	-0.15
[1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 1 0 0 1 0]	4.00	4	0.00
[0 1 1 1 1 1 1 1 1 0 0 1 1 1 0 0 1 1 1 1]	2.70	3	-0.30
[0 1 1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0]	2.99	3	-0.01
[1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 0 0]	2.99	3	-0.01
[0 0 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 1]	3.64	4	-0.36
[1 1 1 0 0 0 0 1 0 0 1 1 1 1 1 1 1 1 1 1]	3.07	3	0.07
[1 1 1 1 1 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0]	3.88	4	-0.12
[0 1 1 0 0 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0]	3.32	3	0.32
[1 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 1 1 0]	4.20	4	0.20
[1 1 1 0 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0]	2.69	3	-0.31
[0 0 0 1 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 1]	3.07	3	0.07
[0 0 1 1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1]	2.92	3	-0.08
[0 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 1 1 0]	2.90	3	-0.10
[1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 0 0]	2.78	3	-0.22
[1 0 0 1 1 1 1 1 1 0 0 1 1 1 0 0 1 1 1 0]	3.91	4	-0.09
[0 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 1 1 0 0]	3.25	3	0.25
[0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 1]	3.13	3	0.13
[0 0 0 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 0]	2.93	3	-0.07
[0 0 1 0 0 0 0 1 0 0 1 1 1 1 0 0 0 0 0 0]	3.05	3	0.05
[1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1]	3.05	3	0.05
[1 0 0 0 0 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0]	3.11	3	0.11
[0 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 1 1 1 0]	2.79	3	-0.21
[0 0 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0 0 1 0]	3.01	3	0.01
[0 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 0 0 0 1]	3.99	4	-0.01
[1 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1]	3.00	3	0.00
[0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 0 1 1 1 0]	3.69	4	-0.31
[1 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1]	3.02	3	0.02
[1 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1]	3.09	3	0.09
[0 1 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 1 1 1]	2.88	3	-0.12
[0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1]	2.30	2	0.30
[0 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0 1 1]	2.99	3	-0.01
[0 0 1 1 1 1 1 1 0 0 1 1 1 0 0 0 0 1 1 1]	2.88	3	-0.12
[0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0]	3.87	3	0.87
[1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1]	3.18	3	0.18
[0 0 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1]	1.89	2	-0.11
[1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 0]	2.20	2	0.20
[0 0 1 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 1 0]	2.90	3	-0.10
[1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0]	2.91	3	-0.09
[0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 1 1 1 1 1]	3.17	3	0.17
[1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0]	2.83	3	-0.17
[0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0]	2.90	3	-0.10
[1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 1 1 1 0]	4.11	4	0.11
[0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0]	1.02	1	0.02
[0 0 0 0 0 0 0 1 1 1 0 0 1 0 0 1 1 1 1 1]	3.12	3	0.12

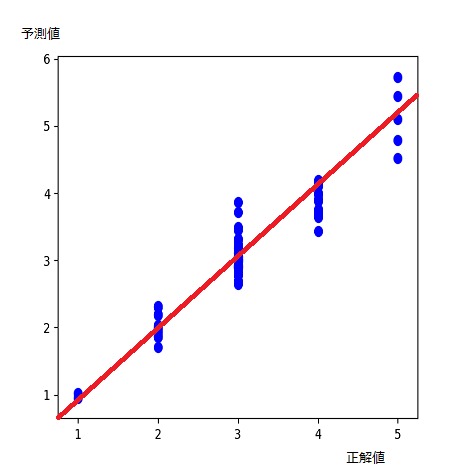
##正解値に対する予測値のバラツキ：

　　学習回数 100000エポックの場合
　　（赤い直線 x=y 上にプロットされるのが理想。）

　　参考: 学習回数 100エポックの場合
　　（すでに、なんとなく学習成果が出始めている。）

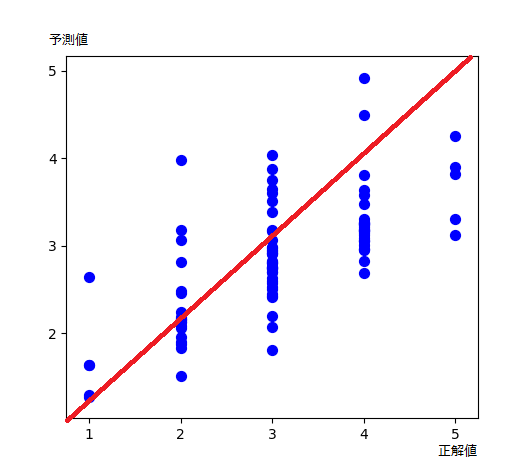
　各正解値に対するデータ数の違い（正解値１や５のデータが少ない）は、データ生成アルゴリズムに影響されている。

#ちなみに2次元バージョンを追加

https://github.com/uminor/counter
-> counter2d.py

10×10 の２次元だけど、モデル的には100次元の入力。
(本来は画像で入力して配列に変換すればいいんだろうけど、今回は最初から２次元配列で)

入力データ例：
[
[ 1. 1. 1. 0. 0. 0. 0. 0. 1. 1.]
[ 1. 1. 1. 0. 0. 0. 0. 0. 1. 1.]
[ 1. 1. 1. 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 1. 1. 0. 1. 1. 1. 0.]
[ 0. 0. 1. 1. 1. 0. 1. 1. 1. 0.]
[ 0. 0. 1. 1. 1. 0. 1. 1. 1. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
]　　→　正解は 5　(すなわち、1 の島が５個)

[
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[ 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
]　　→　正解は 4　　(すなわち、1 の島が４個)

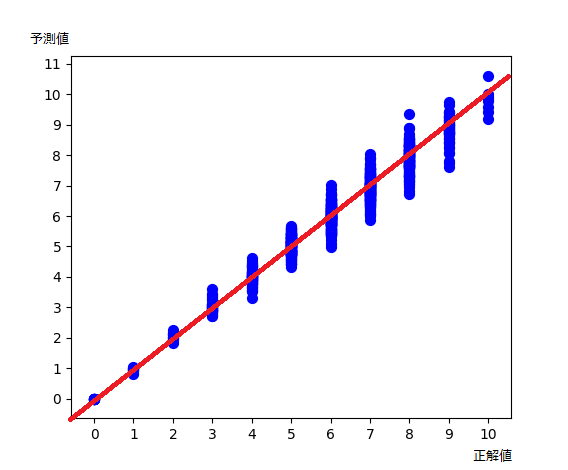
###まあ綺麗な結果になった。
（学習データ9000, 検証データ1000, 学習回数1000エポック）

結論というか

当初目的であった、ニューラルネットワークが「パターンの数を数える」ことのポテンシャル としては、「結構いけてる」 と評価。
実用面でいうと、データの前処理次第でいろいろ使えそうかも、という感じか。
まあ、こういうことは今まで世界中で試されてきたんだろうけど、ググッても見つかりにくい（特に keras 応用において）ので掲載してみた。
そういえば、パターンの数 1個,2個,3 個で学習させて 4個,5個　を予測させる(外挿というか帰納というか)というのは、やってないなあ。これってある意味重要か[2]。あとでやってみるか。。

#参考文献
[1]
平野 廣美(2008-2009)『C++とJavaでつくるニューラルネットワーク』パーソナルメディア.
pp.74　から引用：

入力マトリックスのマス目をランダムにOnしていき、Onされたマス目の数が "たくさん" なのか、"そんなもん" なのか、"すこし" なのかを学習させた後、テストパターンを与えて判定させてみます.
残念ながら、この場合はうまく判定してくれません.」```

<a name="2">[2]</a>
[1]と同じ文献 pp.75 から引用：
```「チンパンジーにものを数えさせる実験がありますが、たとえば、１～６ を学習させた後、次の７をその延長で数えることはできないようです.」```


<a name="3">[3]</a> 
市橋秀友　他『監視カメラとFCM識別器による屋外駐車場の空きスペース検出システム』大阪府立大学 他.
https://www.jstage.jst.go.jp/article/fss/25/0/25_0_128/_pdf
（但し、これはニューラルネットを用いた例ではなさそう。「噂を聞いた」のはこれとは別件。）