（いきなり注）
- この記事で述べることは筆者独自の考察であり、一般的に言われていることではない、かもしれない。
- あるいは、先人が既に通った道に過ぎない、かもしれない。
- ここで扱う機械学習のモデルは、
ニューラルネットワーク ＞ シーケンシャルモデル ＞ 多層パーセプトロン、
を想定。
（以下ＮＮと略す）
１．情報量の次元、と、情報が表現される空間の次元
ここでいう「情報量」とは、実数を要素に持ち、ある情報を構成するベクトルの要素の数（次元数）、という意味で用いる。
「情報量の次元」と「情報が表現される空間の次元」は混同されるべきではない。
例えば、２次元空間上の線分 L を考える。
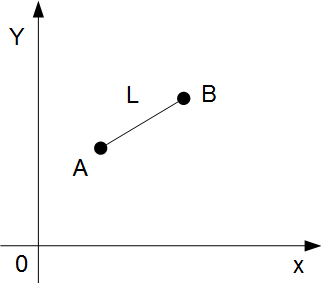
点Ａと点Ｂを結ぶ線分Ｌは、
点Ａの座標（Xa , Ya）と 点Ｂの座標（Xb , Xb）によって表現される。
したがって２次元空間における線分Ｌは（Xa , Ya, Xb , Yb）という４次元
ベクトルによって表現することができる。
これは、線分Ｌの情報量が４次元である、ということもできる。
なお、線分Ｌは、「２次元のディジタルなパターンによって近似」
することができる。こんなぐあいである。
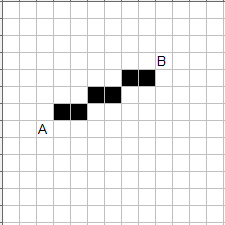
同様に写真のようなディジタル画像データは、２次元空間に配置される
画素（ピクセル）の集まりによって表現される。
例えば、この２次元画像 
は、
横１００画素 × 縦１００画素 ＝ １万 画素
で表現され、ＲＧＢの３色で表現されたカラー画像であれば、その３倍
すなわち ３万 の情報量を持つ。
これは、上記画像は情報量が３万次元のベクトル
（X1, X2, X3, ・・・ X30000）
によって表現されている（非圧縮時）、ということもできる。
２．「パターン」から「ベクトル」を抽出する。
- 機械学習でいう「分類」は、 パターン から ベクトル を抽出（出力）すること、と解釈する。
- 例：
- 犬らしき画像（＝画素の パターン ）、
を入力すると、 - [犬、猫、猿] = [70%, 10%, 20%] というような確率の ベクトル を出力する。
( この出力では、入力画像が「犬」である確率が最も高いことを示している。)
- 複雑な画像 パターン から より単純な ベクトル を抽出することは、情報の圧縮 （あるいは次元の圧縮？）ともいえる。
- 例えば、上記の犬らしき画像は、上述の通り 3万 次元の情報量を持つ。
- 上記の分類では、３万次元を３次元に圧縮している。
- 画像の分類のほか、テキスト分類も同様に、パターンからより単純なベクトルを抽出するものであり、情報の圧縮といえる。
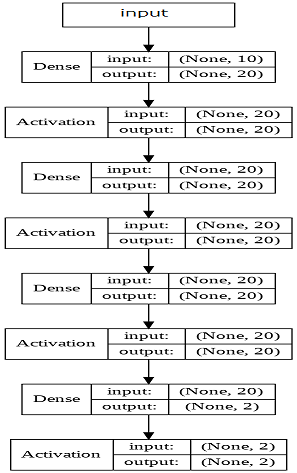
- ここで、おもいきり単純化した例として、１０次元の情報量を持つパターンを２次元に圧縮してみる。
- 例えば、[ 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. ] という(１と0だけの)パターンは、
１次元空間で表現されているが、情報量としては１０次元である。 - よく見ると、５番目から７番目まで 1 が並んでいる。
- つまり [ 5番目, 7番目 ] というベクトルを抽出（言い換えれば２次元に圧縮）することができる、と考えられる。
- これは、よくある２次元空間内のベクトル (x, y)=(5, 7) とは意味が異なる。
（いわば、１次元空間内の２箇所の位置を指す２個の位置ベクトル、と言ってしまおうか？）
-
注：多くのプログラミング言語では配列の最初をゼロ番目と数えるので、以後これに準じて、上記の場合のベクトルを、[ 4, 6 ] と表記する。（[from:4, to:6] と解釈していただきたい）
-
こういうデータ処理は、ＮＮじゃない伝統的なアルゴリズムが得意とするところ。
-
しかしここでは、大いなる野望 のために、あえてＮＮで実装する。
-
この１０次元のパターンに対して、まあまあシンプルなＮＮモデルを構築して学習・評価してみた。
- ソースコードの公開場所は後述。
- Activation は いずれもsigmoid関数を用いている。）
- 前述の１０次元のパターンの総数は、わずか５５個である。(10+9+8+ ・・・+1=55)
このパターンを総当たりで順次生成し、７の倍数のタイミングで生成されたものを評価用データ、その他を学習用データとして 3000 エポック学習。 - 評価用データを用いた推定結果は次のようなかんじ。
| No. 0: [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] : 入力パターン [' 1.30', ' 1.44'] ：推定したベクトル [' 0.00', ' 0.00'] ：真のベクトル |
| No. 1: [1. 1. 1. 1. 1. 1. 1. 1. 0. 0.] : 入力パターン ['-0.07', ' 6.96'] ：推定したベクトル [' 0.00', ' 7.00'] ：真のベクトル |
| ： 中略 ： |
| No. 6: [0. 0. 0. 0. 0. 1. 1. 1. 0. 0.] : 入力パターン [' 4.95', ' 6.97'] ：推定したベクトル [' 5.00', ' 7.00'] ：真のベクトル |
| No. 7: [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.] : 入力パターン [' 6.09', ' 6.10'] ：推定したベクトル [' 7.00', ' 7.00'] ：真のベクトル |
-
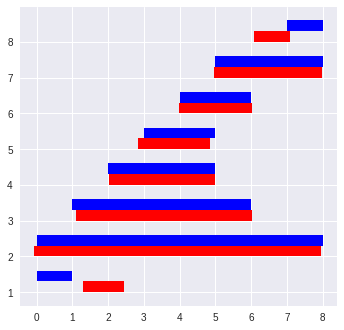
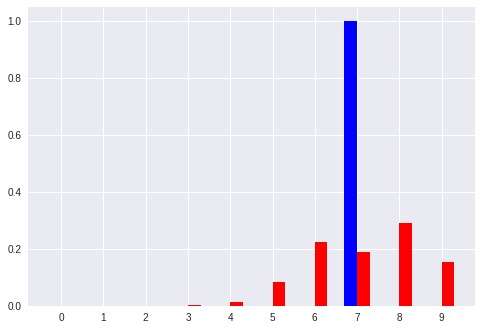
（データの羅列っておもしろくない。）ので上記の評価結果を視覚化してみる。
（青は正解値、赤は推定値、それぞれのベクトルを視覚化したもの）
-
見た感じでは、赤い棒が青い棒に大体追随している。（つまりパターンから、ある程度をベクトル抽出できているように見える。）
-
但し、小さいパターン（長さ＝１）では、開始点に１ぐらいの誤差が生じている。
（このモデルでは、比較的小さいパターンは認識しずらいということか？）
３．「ベクトル」から「パターン」を生成する。
-
上記により、
「パターンからベクトル抽出」 すなわち データ圧縮、ができたので、逆に、
「ベクトルからパターン生成」 すなわち データ復元、もできるのではないか？ -
しかし、いきなり、こういう復元は無理があるよな～。
[犬、猫、猿] = [100%, 0%, 0%] → -
「画像の辞書」みたいなものを持っておけばできそうだど、そういうことじゃない。
-
そこでここでも、おもいきり単純化して、２次元のベクトルから１０次元の情報量を持つパターンを復元することを考える。
-
例： [ 5, 7 ] → [0. 0. 0. 0. 0. 1. 1. 1. 0. 0.]
-
こういうデータ処理は、ＮＮじゃない伝統的なアルゴリズムが得意とするところ。
-
しかしここでも、大いなる野望 のために、あえてＮＮで実装する。
-
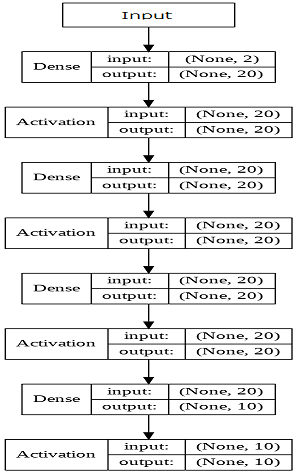
モデル
- ソースコードの公開場所は後述。
- ここでも、Activation は いずれもsigmoid関数を用いている。
-
ベクトルの総数もパターンと同様、わずか５５個である。(10+9+8+ ・・・+1=55)
このパターンを総当たりで順次生成し、７の倍数のタイミングで生成されたものを評価用データ、その他を学習用データとして 30000 エポック学習。 -
評価結果のデータと、それを視覚化したグラフ
- （青は正解値、赤は推定値、それぞれのベクトルを視覚化したもの）
-
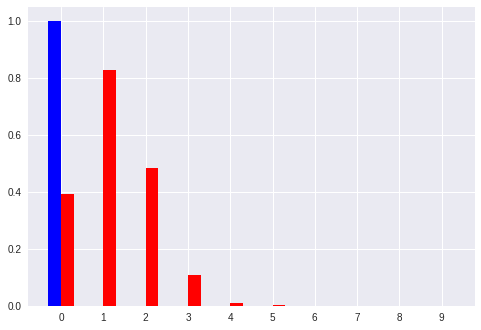
No. 0 [0 0]：入力ベクトル
[' 0.39', ' 0.83', ' 0.48', ' 0.11', ' 0.01', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：推定したパターン
[' 1.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：真のパターン
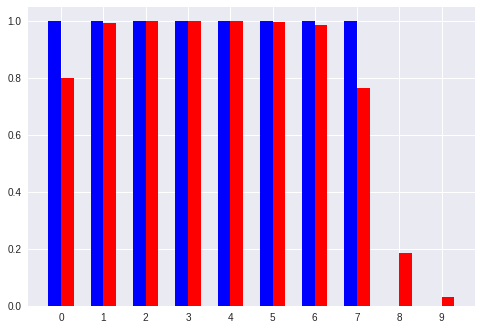
No. 1 [0 7]：入力ベクトル
[' 0.80', ' 0.99', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 0.98', ' 0.76', ' 0.18', ' 0.03'] ：推定したパターン
[' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00'] ：真のパターン
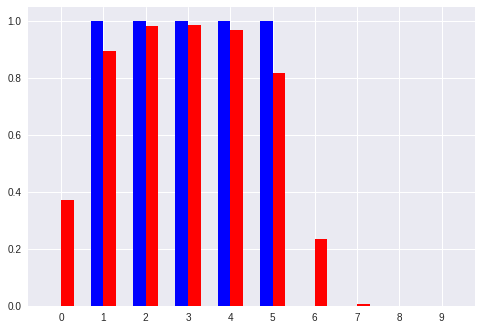
No. 2 [1 5]：入力ベクトル
[' 0.37', ' 0.90', ' 0.98', ' 0.99', ' 0.97', ' 0.82', ' 0.23', ' 0.01', ' 0.00', ' 0.00'] ：推定したパターン
[' 0.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：真のパターン
No. 3 [2 4]：入力ベクトル
[' 0.04', ' 0.28', ' 0.77', ' 0.87', ' 0.72', ' 0.44', ' 0.06', ' 0.00', ' 0.00', ' 0.00'] ：推定したパターン
[' 0.00', ' 0.00', ' 1.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：真のパターン
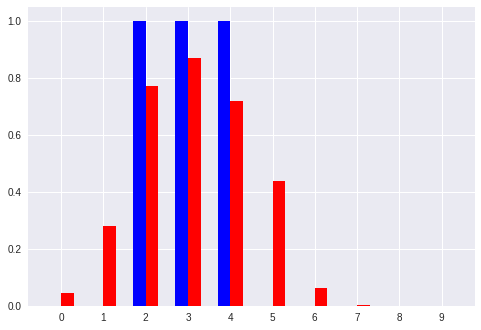
No. 4 [3 4]：入力ベクトル
[' 0.01', ' 0.03', ' 0.35', ' 0.71', ' 0.66', ' 0.54', ' 0.14', ' 0.00', ' 0.00', ' 0.00'] ：推定したパターン
[' 0.00', ' 0.00', ' 0.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：真のパターン
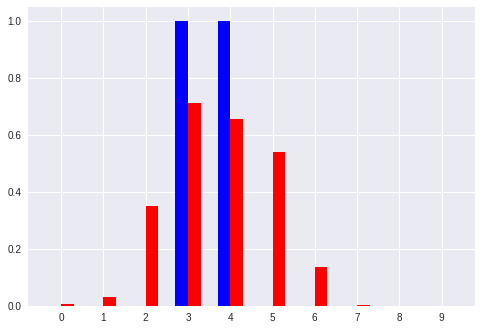
No. 5 [4 5]：入力ベクトル
[' 0.00', ' 0.00', ' 0.07', ' 0.41', ' 0.62', ' 0.70', ' 0.43', ' 0.05', ' 0.01', ' 0.00'] ：推定したパターン
[' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00'] ：真のパターン
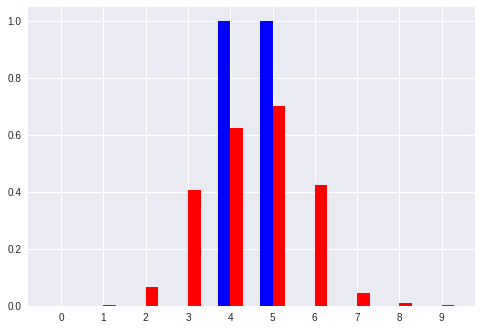
No. 6 [5 7]：入力ベクトル
[' 0.00', ' 0.00', ' 0.00', ' 0.03', ' 0.28', ' 0.63', ' 0.76', ' 0.67', ' 0.45', ' 0.18'] ：推定したパターン
[' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 1.00', ' 1.00', ' 1.00', ' 0.00', ' 0.00'] ：真のパターン
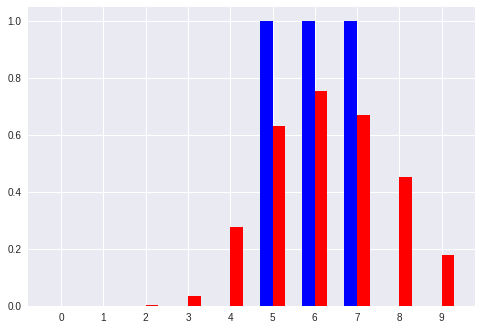
No. 7 [7 7]：入力ベクトル
[' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.01', ' 0.08', ' 0.22', ' 0.19', ' 0.29', ' 0.15'] ：推定したパターン
[' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 0.00', ' 1.00', ' 0.00', ' 0.00'] ：真のパターン
-
以上のように、ベクトルからパターンへの変換を学習したモデルでは、「キリッとした正解パターン（青色）」 に対して **「ボヤっとした推定パターン（赤色）」**を出力している。
-
「キリッと」「ボヤっと」というような感覚的な表現はパターンにおける コントラスト の大小と言い換えることができるかも。
-
ここでも、比較的小さいパターン（No.0 や No.7）では誤差が大きい感じに見える。
-
今回は ＮＮの「全結合」のみのモデルを使ったが、コントラストの問題だとすると、ひょっとすると「畳み込み層」の導入により精度が改善される可能性があるかも。
- 画像認識では「畳み込み層」は、学習によりコントラストを高める効果を持つことが多い。
- しかし今回のような１次元配列的パターンで畳み込み層を簡単に実装する方法がよくわかってない・・
４．オートエンコーダ
- 以上のような、
- 「パターンからベクトル抽出」 すなわち データ圧縮、
-
「ベクトルからパターン生成」 すなわち データ復元、
を直列に並べたもの:
（パターン → ベクトル → パターン）
が、「オートエンコーダ」 と呼ばれるモデルに相当する（・・たぶん）。
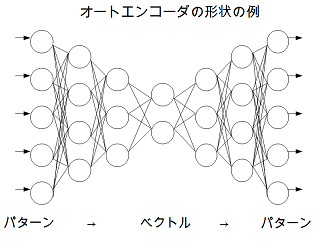
- 本稿は、オートエンコーダの機能を単純化し、分解して調べたもの、とも言える（・・かもしれない）。
- ただ、「オートエンコーダ」が、パターン → ベクトル → パターン、という変換、として語られることは一般的ではない。（・・気がするので、ここで語ってみた。）
- 改めてオートエンコーダの形状を眺めると、パターンとベクトルは明確に分けられるものではなく、パターン的なレイヤーからベクトル的なレイヤーに、またはその逆に、徐々に変換されるものであるように思える。（仮説）
５．大いなる野望について
・・は、今後の投稿によって次第に明らかにされていく予定である。