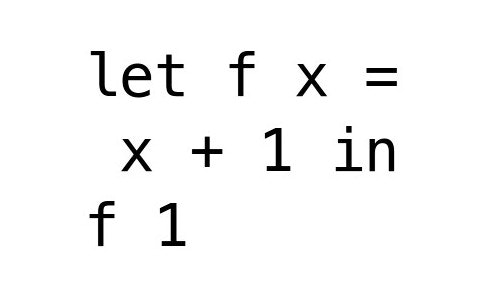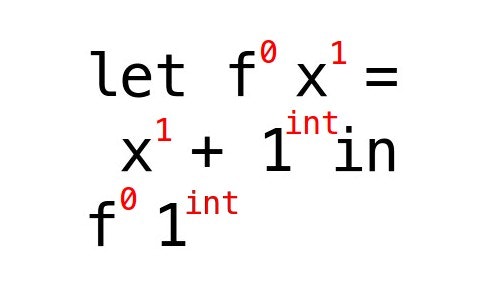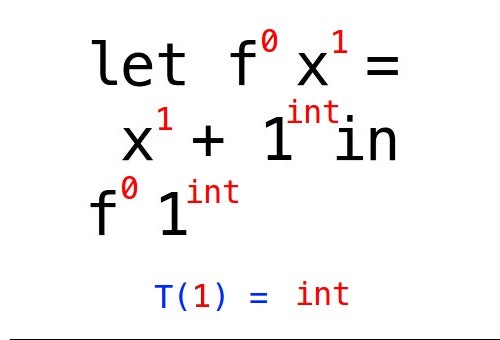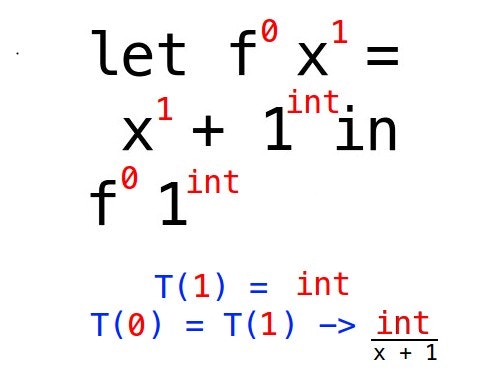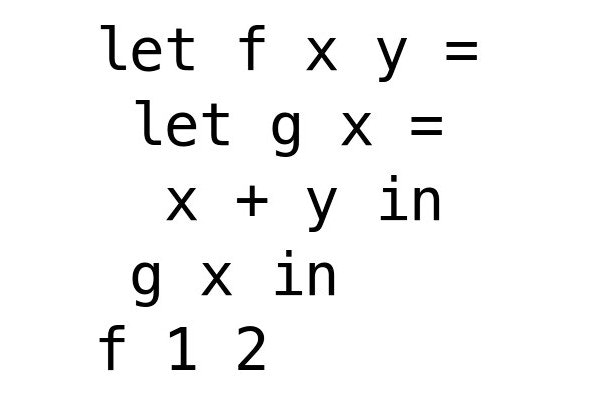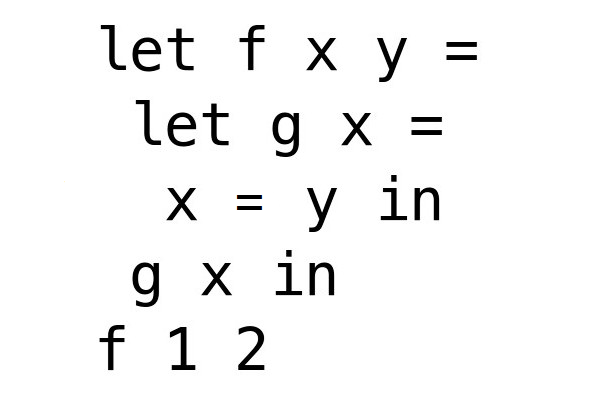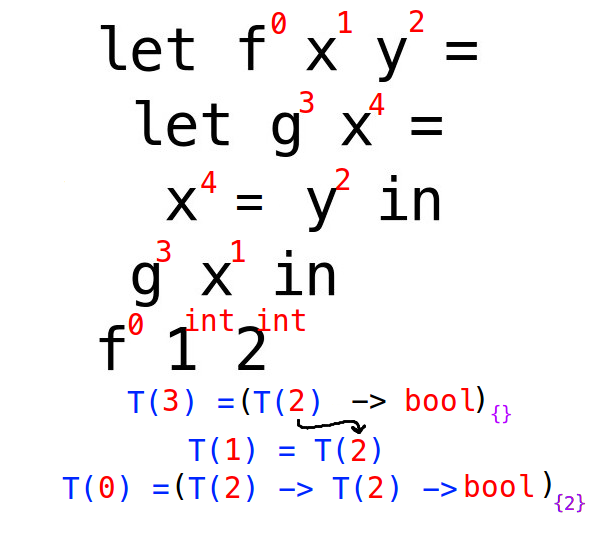人でもわかる型推論

追記: この記事を書いてから早2年弱。今は数式のほうがわかりやすいなあと思うようになりました。

これは何？

• この記事は、最近 Hindley Milner (Algorithm W) 型推論を理解したばかりの私が、型推論のことをなるべくわかりやすく解説するものです。
• 簡略化したOCamlのようなコードが登場します。
• わかりやすさ重視で書いていくつもりなので、専門用語(自由変数とか)はあまり出てきません。 間違いなどあったらコメントしていただけると幸いです。

まずは単相から

ここからは図を使って説明していきます。(ビジュアルなほうがわかりやすいハズ)

とても簡単な例

以下にとても簡単なコードを示します。

見ればわかりますが、xの型はintですね。
ですが、どのようにしてintだとわかったのでしょうか。

すでにわかっていることを書き出しだしてみました。リテラルの右肩を見てください。
1の型は当然ながらint、xの型はとりあえず0というidをつけておきました。このidが重要な役割を果たします。

let x = y という式があったとき、xとyの型は当然ながら等しくなります。
したがって、先ほどのidが0のxの型はintということになります。
以下のT(id)はidがidの変数の型を表しています。

T(0) = intとなりました。
print_intの引数にxがありますが、xのidは0なので、T(0) = intよりxの型はintだとわかります。

関数

以下の画像を見てください。

先ほどの例よりも少し難しくなりました。先に言っておくと、fの型はint -> int、xは当然ながらintですね。
まずは先ほどと同じようにわかることを書き出してみます。

let f x y = x + yという式があったとき、fの型はxの型 -> yの型 -> x + yの型と等しくなります。
let式の中身を見てみると、x + 1とあります。これはxの型は1の型、すなわちintと等しいということになります。

x + 1の型はintだとわかりました。するとfの型はint -> intだとわかります。
xの型 -> x + 1の型ということですね

関数2

もうちょっとややこしく。

わかっていることを書いて。

letの式の中身を評価していきます。

gの中のx + yはint。
よってgはxの型 -> x + yの型でint -> int。

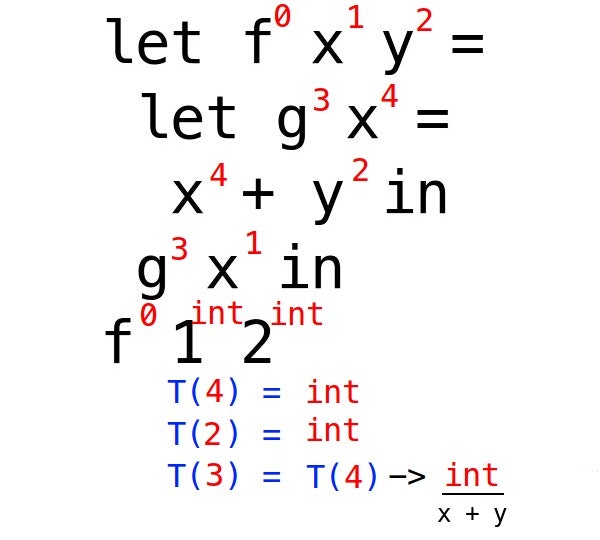
fの中はlet g x = x + y in g xですが、結局はg xです。
gはint -> intなのでgの引数のxはint、g xもintとわかります。
結果的にfの型はxの型 -> yの型 -> g xの型でint -> int -> intとわかります。

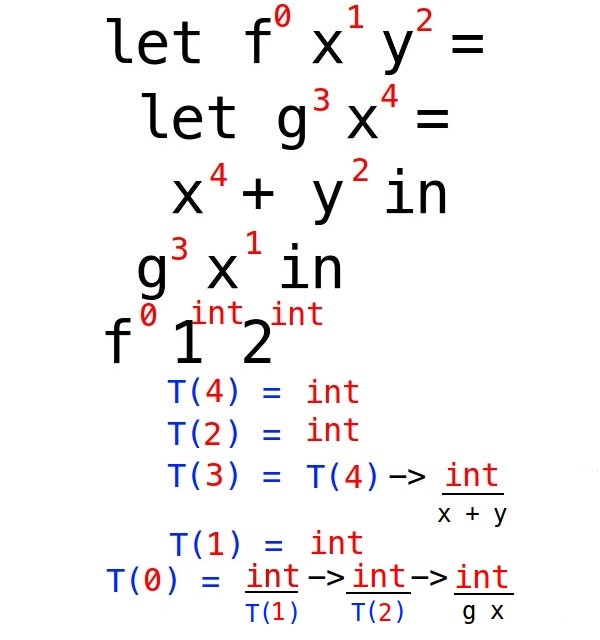
以上、単相型推論の簡単な解説でした。

そして多相へ

さて、多相になるとちょっと難しくなります。

一番最初の例ですが、ちょっと複雑なコードを示します:

わかることを書き出します:

続いて、単相のときと同じように型を推論してみます。

一見正しく型推論できているようですが、
このままだとf 1 2を評価したときに T(0)がint -> int -> boolとなってしまい、以降fが呼び出された時に多相性が失われてしまいます。fが'a -> 'a -> boolだったはずなのに、'aがintで上書きされてしまいます。
f 1.2 3.4などとすると型エラーになるわけです。これではいけません。

ここからは多相型推論の手順を説明します。
下の図のT(2) -> boolの右下をみてください。

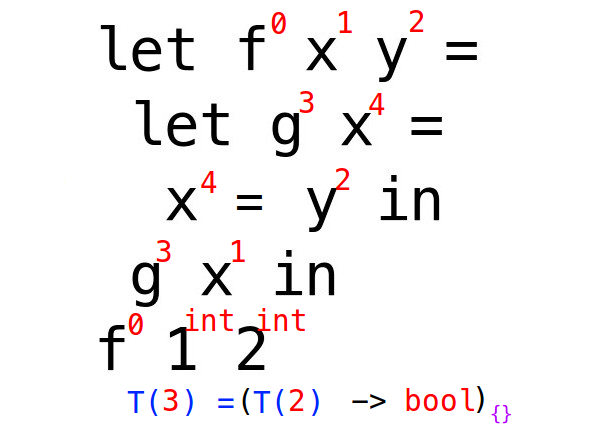
何か{}という物がついていますね。ここにはその型に含まれるidから, その型環境に含まれるすべての型のそれぞれに含まれるidからそのそれぞれの型の{}に含まれるidを取り除いたもの, を取り除いたものが含まれます。

... 多分今の説明で理解できた人は少ないと思います ...
ここからは、多相型推論を理解する上で知っておかなくてはならないことをまとめます。

まず型環境というのは、簡単に言えば、ある型を推論する時点ですでに存在が知られている型の集合です。
上の図で3行目までを読み込んでgの型を推論する場合なら、f, x [id=1のやつ], yがそうです。gの型を推論するのですから、gやx [id=4のやつ]は含まれません。

そして肝心の {} の役割ですが、ある{}を持つ型は、instantiateされるときにその{}に含まれるidと同じidの型を新しいidの型に変えます。instantiateというのは、ある変数が使われるときに、型の多相性を実現するために、その変数の型に今説明した手順を実行することです。図に示すと次のようになります:

T(0) -> T(0) -> T(0)という型があったとして、{0}がくっついているなら、その中のT(0)を全て新しいT(1)で置換します。T(1)というのは、まだ使われていないidならなんでも良いはずです。

そして、先ほどの長くて難しい文章、{}に含ませるidを決定する操作のことをgeneralizeといいます。汎用的になるんですね。すべての変数はgeneralizeされて{}を持つことになります。

さて、ここまでで一応、多相型推論はできるようになったはずです。やってみましょう。
もう一度先ほどの画像です:

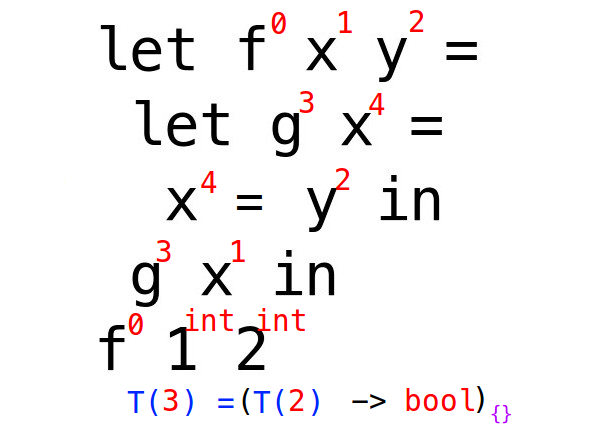
ここまででgの型がわかっています。次はfですね。
画像内のコードの４行目でx [id=1]の型が決定されます。
letでgが定義されているのでgの型には{}が付き、gにxが適用されるのでgがinstantiateされます。
{}の中身を表で計算してみましょう。

集合名	中身
型環境に含まれるすべての型	T(0), T(1), T(2), int, bool
型環境に含まれるすべての型のid	0, 1, 2
型環境に含まれる型の{}に含まれるもの
型環境に含まれるすべての型のidから{}に含まれるものを除いたもの	0, 1, 2
gの型に含まれるid	2
gに含まれるidから, その型環境に含まれるすべての型のそれぞれに含まれるidからそのそれぞれの型の{}に含まれるidを取り除いたもの, を取り除いたもの

よって、{}の中身には何も入りません。

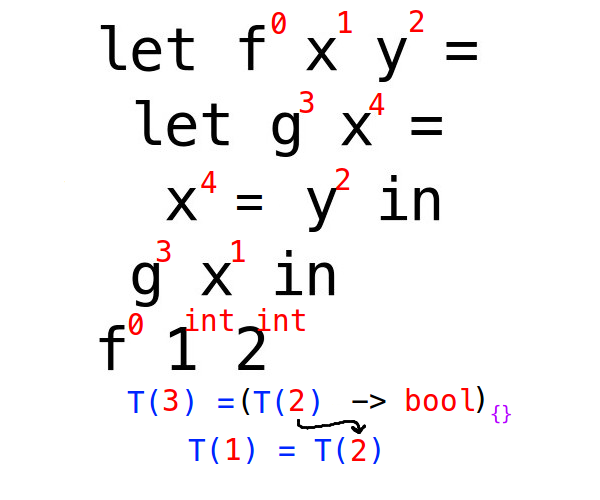
gがinstantiateされましたが、{}の中身が空なのでこの場合特に変化はありません。
fの返却型はg xよりboolです。
このままだと、fの型はT(2) -> T(2) -> boolですが、{}のことを思い出してみましょう。
あのgeneralizeの長い難しい文章通りに手順を踏めば、{2}という結果が得られるはずです。
やってみましょう。

集合名	中身
型環境に含まれるすべての型	int, bool
型環境に含まれるすべての型のid
型環境に含まれる型の{}に含まれるもの
型環境に含まれるすべての型のidから{}に含まれるものを除いたもの
fの型に含まれるid	2
fに含まれるidから, その型環境に含まれるすべての型のそれぞれに含まれるidからそのそれぞれの型の{}に含まれるidを取り除いたもの, を取り除いたもの	2

正しく{2}という結果が得られました。

こうすれば、f 1 2を評価した時にはfの型はT(5) -> T(5) -> boolと評価されて多相性が実現されます。intで上書きされないんですね。

以上が多相型推論の説明でした。この記事自体、急いで書いたので(ただいま 12/19 20:00)わかりづらいところや間違っている部分もあると思います。
コメントお待ちしております。