JavaScriptで無限に再帰したい

再帰関数は、自分自身を呼び出す関数です。再帰関数はプログラミングにおける極めて有用な道具であり、再帰関数を用いることで綺麗に書けるプログラムは山のようにあります。

ところが、JavaScript を始めとする一部のプログラミング言語では、再帰の回数に制限があります。その回数を超えて深く再帰しようとするとエラーが発生します。

以下のコードで再帰できる回数を数えてみましょう。

function countRecursion() {
  let count = 0;
  function rec() {
    count++;
    rec();
  }
  try {
    rec();
  } catch {
    console.log(count);
  }
}

環境によって異なると思いますが、自分の環境では15721と表示されました。

※追記: 再帰とトランポリンの関係についてご存知の方は、記事最後の追記を読むと記事の内容が一瞬で理解できるかもしれません。

再帰できる回数が足りないことがある

環境によって異なるとはいえ、再帰できる回数が 1 万とかその程度では足りない場合があります。例えば、白黒に塗られたマスの上で色を交互に通って移動可能な異なる色のマスの組の総数を突然求めたくなるかもしれません。

AISing Programming Content 2019 / C - Alternating Path

問題文

$H$行$W$列のマス目があり、各マスは黒または白に塗られています。
各マスの色を表す$H$個の長さ$W$の文字列$S_1, S_2, \dots, S_H$が与えられます。 マス目の上から$i$番目、左から$j$番目 ($1 \leq i \leq H, 1 \leq j \leq W$)のマスが黒く塗られているとき文字列$S_i$の$j$文字目は#となっており、白く塗られているとき文字列$S_i$の$j$文字目は.となっています。

黒く塗られたマス$c_1$と白く塗られたマス$c_2$の組であって、以下の条件を満たすものの個数を求めてください。

• 上下左右に隣り合うマスへの移動を繰り返してマス$c_1$からマス$c_2$へ行く方法であって、通るマスの色が黒、白、黒、白・・・と交互になっているものが存在する。

制約

• $1 \leq H, W \leq 400$
• $|S_i| = W$ ($1 \leq i \leq H$)
• 各$i$ ($1 \leq i \leq H$)に対して、文字列$S_i$は文字#と文字.だけからなる。

入力

入力は以下の形式で標準入力から与えられる。

H W
S1
S2
…
SH

出力

答えを出力せよ。

※ 茶番に付き合いたくない方は次の節「自前でスタックを管理する」まで飛ばしても大丈夫です。

この問題を解くには、マス目たちを黒、白、黒、白……という移動で行き来可能なグループ（連結成分）に分けることを考えます。そのグループ内に黒のマスが$b$個、白のマスが$w$個あった場合、グループ内のどの黒いマスからどの白いマスに行くこともできますから、そのグループ内に条件を満たす組み合わせは$b \times w$個あることになります。また、異なるグループ同士を行き来することはできませんから、これ以外のマスの組み合わせを考える必要はありません。よって、各グループに対して$b \times w$を求めてそれを全部合計すると求める答えになります。

なお、筆者は競プロに関してはクソザコなので解法に対するつっこみなどはご容赦ください。

さて、上記の方法でこの問題を解くには、マス目たちをグループに分ける処理を書く必要があります。そのための1つの方法が深さ優先探索です。`そして、深さ優先探索は再帰関数を使って簡単に書けることが知られています。

下のコードでは、searchという再帰関数を定義しています。これは引数xとyを受け取り、そのマスを含むグループ内の黒いマスの数blackと白いマスの数whiteを[black, white]という配列にして返します。関数searchは今の位置の上下左右のうち移動可能な方向（すなわち今の場所と同じグループに属する方向）に探索を行い、それらの結果と今の位置の情報を足すことでblackとwhiteを計算します。ただし、すでにカウント済みのところを再度カウントしないように、既にカウントしたかどうかという情報を配列visitedに記録しています。

素晴らしい回答コード

function main(input) {
  // 標準入力を行ごとに分解
  const lines = input.split("\n");
  // HとWを受け取る
  const [H, W] = lines[0]
    .match(/^(\d+)\s+(\d+)$/)
    .slice(1)
    .map(i => parseInt(i, 10));
  // Sたちを取り出す
  const S = lines.slice(1, H + 1);

  // 各マスを既に訪れたかどうかを記録する2次元配列を作成
  const visited = Array.from({ length: H }, x => new Array(W).fill(false));
  // 各連結成分を深さ優先探索
  let result = 0;
  for (let x = 0; x < W; x++) {
    for (let y = 0; y < H; y++) {
      const [black, white] = search(x, y);
      result += black * white;
    }
  }
  // 答えを出力
  console.log(result);
  function search(x, y) {
    if (visited[y][x]) {
      // このマスは探索済みだ
      return [0, 0];
    }
    visited[y][x] = true;

    let black = 0,
      white = 0;
    // 現在の位置をカウント
    const here = S[y][x];
    if (here === "#") {
      black++;
    } else {
      white++;
    }
    // 上下左右を探索
    for (const [dx, dy] of [[-1, 0], [1, 0], [0, -1], [0, 1]]) {
      const nextx = x + dx,
        nexty = y + dy;
      if (nextx < 0 || nexty < 0 || nextx >= W || nexty >= H) {
        continue;
      }
      // 隣が自分と異なる場合のみ探索可能
      if (S[nexty][nextx] !== here) {
        const [b, w] = search(nextx, nexty);
        black += b;
        white += w;
      }
    }
    return [black, white];
  }
}

// 標準入力を文字列で受け取ってmain関数を実行
main(require("fs").readFileSync("/dev/stdin", "utf8"));

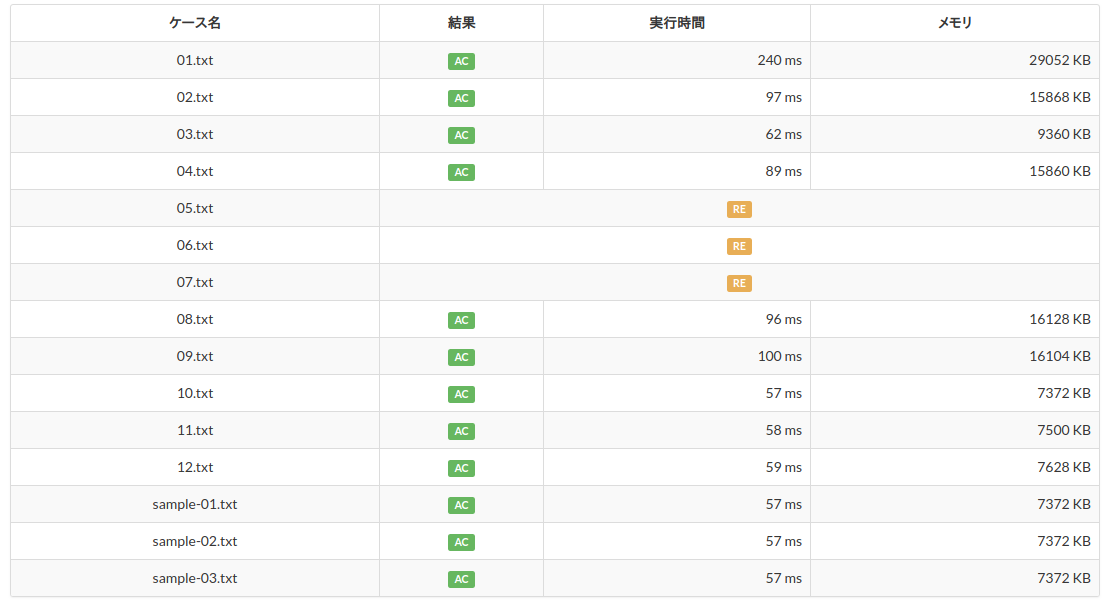
では、早速このコードを提出してみましょう。

提出 #4015744

ACは正解ということですが、なんかREというのが3つありますね。これはランタイムエラーのことです。

そうです。これこそが正しく再帰の回数が足りないということです。上の制約というところをよく見ると$1 \leq H, W \leq 400$と書いてありますから、マスは最大で$400 \times 400$、すなわち16万個あることになります。上のアルゴリズムは1マス探索するたびに1回再帰しますから、この上に万単位の大きさのグループが存在する場合は再帰の上限を超えてしまうわけです。これが実行時エラーとなり、REという結果になっています。

前置きが長くなりましたが、この記事では再帰の上限を超えてしまうという問題を解決することを目標とします。

自前でスタックを管理する

今回のアルゴリズムは深さ優先探索でしたが、深さ優先探索は再帰以外にもスタックというデータ構造を用いて実装できることが知られています。スタックというのは、要素を追加したり取り出したりすることができ、取り出すときは最後に追加されたものから逆順に取り出されるというデータ構造です。

これを一歩進めて、そもそも再帰関数一般はスタックを用いることでループに変換することができます。しかし、アルゴリズムを再帰関数を使ったものからループに使ったものに書き換えるのはちょっと頭を使う作業ですし、せっかく直感的な方法があるのだから再帰を使って書きたいものです。

そこで、この記事では再帰を用いたアルゴリズムをなるべく形を変えずにループに書き換えます。そのために使う道具がジェネレータ関数です。

ジェネレータ関数は、中でyield式という特殊な式を用いることができる関数です。yield式が実行されると関数がその場で中断され、関数を呼び出した側に処理が戻ります。その後ジェネレータ関数を再開することも可能です。その際関数に対して値を渡すことができ、その値はyield式の返り値として利用されます。

今回のアイデアは、再帰関数を書く代わりにジェネレータ関数を書き、再帰呼出しの代わりにyield式を実行することで再帰の処理を外側に委譲するというものです。委譲される側は関数呼び出しや返り値の扱いをスタックを用いて管理します。

というわけで、新しいコードを示します。

function main(input) {
  // 標準入力を行ごとに分解
  const lines = input.split("\n");
  // HとWを受け取る
  const [H, W] = lines[0]
    .match(/^(\d+)\s+(\d+)$/)
    .slice(1)
    .map(i => parseInt(i, 10));
  // Sたちを取り出す
  const S = lines.slice(1, H + 1);

  // 各マスを既に訪れたかどうかを記録する2次元配列を作成
  const visited = Array.from({ length: H }, x => new Array(W).fill(false));
  // 各連結成分を深さ優先探索
  let result = 0;
  for (let x = 0; x < W; x++) {
    for (let y = 0; y < H; y++) {
      // 再帰関数を呼び出す
      const [black, white] = runRecursive(search, x, y);
      result += black * white;
    }
  }
  // 答えを出力
  console.log(result);
  function* search(x, y) {
    if (visited[y][x]) {
      // このマスは探索済みだ
      return [0, 0];
    }
    visited[y][x] = true;

    let black = 0,
      white = 0;
    // 現在の位置をカウント
    const here = S[y][x];
    if (here === "#") {
      black++;
    } else {
      white++;
    }
    // 上下左右を探索
    for (const [dx, dy] of [[-1, 0], [1, 0], [0, -1], [0, 1]]) {
      const nextx = x + dx,
        nexty = y + dy;
      if (nextx < 0 || nexty < 0 || nextx >= W || nexty >= H) {
        continue;
      }
      // 隣が自分と異なる場合のみ探索可能
      if (S[nexty][nextx] !== here) {
        // 再帰呼出しはyieldで行う
        const [b, w] = yield [nextx, nexty];
        black += b;
        white += w;
      }
    }
    return [black, white];
  }
}

// 標準入力を文字列で受け取ってmain関数を実行
main(require("fs").readFileSync("/dev/stdin", "utf8"));

function runRecursive(func, ...args) {
  // 最終結果を受け取るオブジェクトを用意
  const rootCaller = {
    lastReturnValue: null
  };
  // 自前のコールスタックを用意
  const callStack = [];
  // 最初の関数呼び出しを追加
  callStack.push({
    iterator: func(...args),
    lastReturnValue: null,
    caller: rootCaller
  });
  while (callStack.length > 0) {
    const stackFrame = callStack[callStack.length - 1];
    const { iterator, lastReturnValue, caller } = stackFrame;
    // 関数の実行を再開
    const { value, done } = iterator.next(lastReturnValue);
    if (done) {
      // 関数がreturnしたので親に返り値を記録
      caller.lastReturnValue = value;
      callStack.pop();
    } else {
      // 関数がyieldした（valueは再帰呼び出しの引数リスト）
      callStack.push({
        iterator: func(...value),
        lastReturnValue: null,
        caller: stackFrame
      });
    }
  }
  return rootCaller.lastReturnValue;
}

まず、真ん中あたりにあるsearch関数に注目してください。定義がfunction* search(x, y){ ... }となり、*がつきました。このfunction*宣言がジェネレータ関数の宣言です。search関数の中身は前とほとんど変わりません。唯一の違いは、search(nextx, nexty)という再帰呼び出しがyield [nextx, nexty]というyield式で置き換わっている点です。yield式に渡す値は配列であり、これが再帰呼出ししたい引数リストを表しています。そして、yield式の結果が再帰呼出しの結果として扱われています。

そして、上のほうでsearchを呼ぶ場面は、search(x, y)となっていたのがrunRecursive(search, x, y)となっています。このrunRecursive関数が、裏で再帰呼出しの処理を担当する関数です。定義は上のコードの下のほうにあります。

中で作られているcallStackという配列が自前で用意した関数のコールスタックです。現在処理されている関数呼び出しがスタックの末尾（配列の一番後ろ）にオブジェクトとして追加されます。スタックに乗るオブジェクト（スタックフレーム）はiterator、lastReturnValue、callerプロパティを持ちます。

callerは今の関数呼び出しの呼び出し元、すなわち“親”のスタックフレームへの参照です¹。iteratorは現在処理されているジェネレータオブジェクトです。ジェネレータ関数は呼び出すとジェネレータオブジェクトを返し、ジェネレータオブジェクトのメソッドを用いて関数の実行を制御できるのです。具体的には、iterator.nextを呼ぶとジェネレータ関数の実行が再開されます。引数に渡した値はyield式の返り値となります²。

iterator.nextによって関数の実行を再開した場合、結果は関数の実行が終了する（doneがtrue）か次のyield式に到達して停止する（doneがfalse）かのどちらかです。前者の場合、親のスタックフレームに呼び出しの返り値を記録します。後者の場合、再帰呼出しが行なわれるので新しいスタックフレームを追加します。

一番最初の呼び出しは親が存在しないので、代わりにrootCallerというオブジェクトを入れておきます。全部の処理が終わったら（すなわち、最初の関数呼び出しが終了したら）、rootCallerから結果を取り出して返します。

以上、ざっくりとした説明でしたが、今回定義したrunRecursiveがコールスタックの管理を行うことで擬似的に再帰関数の処理を実行することができました。そのために、再帰関数本体はジェネレータ関数となり、再帰関数を呼び出すのにyield式を用いるというのが今回のアイデアでした。

使いどころがあるようで使いどころがあまり見当たらないジェネレータ関数ですが、たくさん再帰したくなったときに使ってみるのも一興かもしれません。

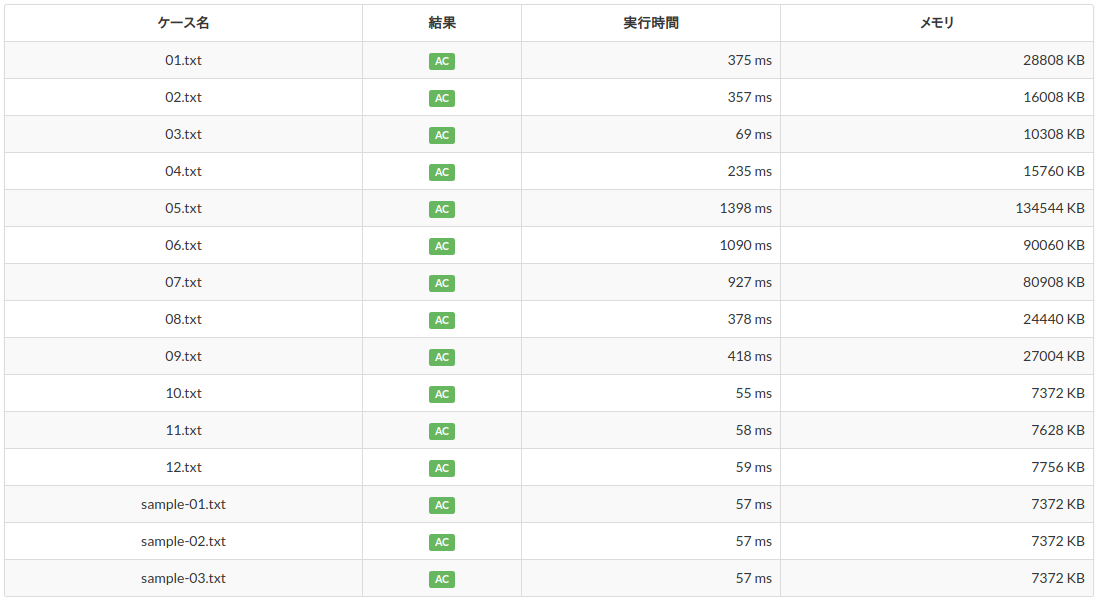
なお、この新しいコードを提出するとちゃんと全部ACになります³。上のコードにより無限に再帰できるようになったことが分かりますね（メモリ量などの制限はもちろんありますが）。

提出 #4015922

結論

???「競プロやるなら**C++**とか使えよ」
ぼく「😇」

追記

この記事を書くまで知りませんでしたが、再帰によるスタックオーバーフローを防ぐ手法はトランポリンと呼ばれているようです。例えば以下の記事が参考になります。

• JavaScript・再帰・トランポリン

軽く調べてみた限りだと、簡単に見つかる資料はいずれも末尾再帰（再帰呼出しの結果をそのままreturnするタイプの再帰）を同様の手法でループに変換するものです。この記事の内容は、末尾再帰以外に対するトランポリンをジェネレータ関数を用いることで行なったということで理解するのがよいでしょう。一般に再帰関数はCPS変換によって末尾再帰に変換できますが、プログラムの分かりやすさの観点からはCPS変換を避けるほうが望ましいのではないかと思います。

追記2

再帰関数をジェネレータ関数に書き換えるところを勝手にやってくれるBabelマクロを作りました。

• 作って理解するBabelマクロ

1. callerは常に今のスタックフレームの1つ前を指していますからこれは不要かもしれません。ただ、インデックスをいじりたくないのと一番最初の場合の場合分けが面倒だったので、参照を持たせる形にしています。 ↩

2. 一番最初の呼び出しのみ対応するyield式がありません。このあたりの細かい事情はfunction.sentで検索してください。 ↩

3. AtCoderのnode.jsのバージョンで動作するようにBabelを用いてプログラムをトランスパイルしてから提出しています。 ↩