LoginSignup
0
0

More than 1 year has passed since last update.

@uene

フーリエ変換と計測：周波数分解能とは

Last updated at Posted at 2023-06-04

はじめに．

FFTをする際は，
Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manual
にある，以下のコードを実行することが多いかもしれません．

from scipy.fft import fft, fftfreq
import numpy as np
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = fftfreq(N, T)[:N//2]
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()

0603_0.png

このコードを見たときにいくつか不思議に思う点があると思います．

  • なぜ[0:N//2]でスライスしているの？
  • なぜ2.0/N * np.abs(yf[0:N//2])と表示しているの？
  • 本当にIFFTで元の信号の戻るの？
  • 振幅スペクトル，位相スペクトルやパワースペクトルとの違いはなに？
  • 振幅が1になってないのはなぜ？

前回の記事では，
「振幅スペクトルと位相スペクトルを導出してみました．」

今回は，周波数分解能について考察し，STFTへの第一歩を踏み出しましょう！

周波数分解能とは．

例えば，以下のようなコードを実行してみましょう．

from scipy.fft import fft, ifft, fftfreq
import numpy as np
import soundfile as sf


T = 4
fs = 8

f1 = 1
f2 = 2
f3 = 2.01

N = int(fs * T)
dT = 1.0 / fs

time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array)+ \
                        0.5*np.sin(f2 * 2.0*np.pi*time_array)+ \
                        np.sin(f3 * 2.0*np.pi*time_array)

fft_result = fft(signal)

amp = np.abs(fft_result / N)

freq = fftfreq(N, dT)

import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import cycler
colors = ['#000000', '#404040', '#808080', '#C0C0C0', '#FFFFFF']

with mpl.rc_context({'lines.linewidth': 2,
                     'lines.linestyle': '-',
                     'font.family': 'Meiryo',
                     'font.size': 15,
                     'axes.spines.left': True,
                     'axes.spines.bottom': True,
                     'axes.spines.top': False,
                     'axes.spines.right': False,
                     'axes.prop_cycle': cycler(color=colors),
                     'axes.xmargin': 0,
                     'axes.ymargin': 0,
                     'axes.autolimit_mode': 'round_numbers',
                     'xtick.top': False,
                     'xtick.bottom': False,
                     'ytick.left': False,
                     'ytick.right': False,   
                     'figure.autolayout': True,
                     'figure.constrained_layout.use': False,
                     'figure.figsize': (6,4),
                     }):
    fig = plt.figure()
    ax = fig.add_subplot()
    ax.plot(time_array, signal)
    ax.set_aspect('auto')
    plt.xlabel('Time[s]')
    plt.ylabel('Amplitude') 
    plt.xlim(0, max(time_array))
    plt.yticks([-3, -2, -1, 0, 1, 2, 3],
                ['-3.0', '-2.0', '-1.0', '            0', '1.0', '2.0', '3.0'])
    plt.show()

    fig = plt.figure()
    ax = fig.add_subplot()
    ax.plot(freq[0:N//2], 2*amp[0:N//2])
    ax.set_aspect('auto')
    plt.xlabel('Frequency[Hz]')
    plt.ylabel('Amplitude')
    plt.xlim(0, max(freq[0:N//2]))
    plt.yticks([0, 0.5, 1, 1.5],
                ['            0', '0.5', '1.0', '1.5'])
    plt.show()

0603_5a.png
0603_5b.png

画像が生成されました，うれしいですね．

不安．

何か不安を感じませんか？

じっくりこの結果を見てください．

えっ．．．．．．．．．．．．．．．

そうなんです．

x(t) = \sin(1 \times 2\pi t) + 0.5\sin(2 \times 2\pi t) + \sin(2.01 \times 2\pi t)

という波形をスペクトル解析したはずなのに，なにかグラフがおかしくないですか？

不安の正体．

この波形は，

周波数（Hz） 1.00 2.00 2.01
振幅 1.00 0.50 1.00

という波形のはずです．

しかし，グラフでは，

周波数 (Hz) 1.00 1.50 1.75 2.00 2.25 2.50 2.75
振幅 1.01 0.02 0.04 1.49 0.04 0.02 0.02

という結果になっています．

結論．

結論から説明すると周波数分解能が甘く，
周波数2.01の振幅が分散してしまっているため，
このような結果になっています．

エネルギーの観点からの考察．

例えば，以下のようなコードを実行してみましょう．

from scipy.fft import fft, ifft, fftfreq
import numpy as np
import soundfile as sf


T = 4
fs = 8

f1 = 1
f2 = 2
f3 = 2.01

N = int(fs * T)
dT = 1.0 / fs

time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array)+ \
                        0.5*np.sin(f2 * 2.0*np.pi*time_array)+ \
                        np.sin(f3 * 2.0*np.pi*time_array)

fft_result = fft(signal)

amp = np.abs(fft_result / N)

print(np.sum(np.power(np.abs(signal),2))/N)
print(np.sum(np.power(amp,2)))

という記事でも示した通り，

\begin{align}
\mathrm{POWER} = \frac{1}{T} \int_{0}^{T} |x[n]|^2 = \sum_{n~=~-\infty}^{\infty} | c_n |^2
\end{align}

が，エネルギーに関して，振幅スペクトル$| c_n |$が満たす式であり，
エネルギーの観点からは，どちらも1.6265072913519325という値であることがわかったため，
エネルギーの観点からは損失していないことがわかります．

周波数分解能という概念．

この結果から，本来

周波数（Hz） 1.00 2.00 2.01
振幅 1.00 0.50 1.00

というエネルギーの分布になるはずが，
何かしらの理由で，正しい分布になっていないため，

0603_5b.png

のような結果になっていると考えられます．

ここで，freq[0:N//2]変数の中身を見てみましょう．

周波数（Hz）
0.00
0.25
0.50
0.75
1.00
1.25
1.50
1.75
2.00
2.25
2.50
2.75
3.00
3.25
3.50
3.75

そうなんです．周波数2.01Hzが存在しません．
つまり，時間が4秒，サンプリング周波数が8Hzという条件では，正しい計測が出来ていないことになります．

ナイキスト定理と周波数分解能にはご注意．

我々は40kHzの信号を計測する際には，サンプリング周波数を
80kHzより大きい値にしなければならいことを学部の授業に習うでしょう．

では，40.001kHzの信号はサンプリング周波数を
80kHzより大きい値にすれば確実に計測できているのでしょうか？

答えは信号長に依るという回答になります．

簡単に以下のような例で考えてみましょう．

サンプリング周波数 (Hz) ナイキスト周波数の範囲 (Hz) 信号長 (秒) 信号点数
8 -4 ~ 4 4 32

の場合，8Hzの帯域を32点で分解しているため，周波数分解能は

\frac{8\mathrm{Hz}}{32\text{点}} = \frac{1\mathrm{Hz}}{4\text{点}} = 0.25\text{[Hz/点]}

であることがわかります．今回のような，2.01Hzの信号を観測したい場合は，
周波数分解能を0.01Hz以上にする必要があります．

解決策．

再度，式に着目しましょう．
サンプリング周波数$f_s$，信号長$\mathrm{T}$，信号点数$\mathrm{N}$，周波数分解能$\Delta f$に関して，

\Delta f = \frac{f_s}{\mathrm{N}} = \frac{f_s}{f_s\times\mathrm{T}} = \frac{1}{\mathrm{T}}

となるので，周波数分解能は信号長の逆数であることがわかります．
つまり，周波数分解能を向上させるためには，信号長を長くすることが必要です．

周波数分解能は信号長の逆数

解決策を実装しよう．

例えば，以下のようなコードを実行してみましょう．

from scipy.fft import fft, ifft, fftfreq
import numpy as np
import soundfile as sf


T = 100
fs = 8

f1 = 1
f2 = 2
f3 = 2.01

N = int(fs * T)
dT = 1.0 / fs

time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array)+ \
                        0.5*np.sin(f2 * 2.0*np.pi*time_array)+ \
                        np.sin(f3 * 2.0*np.pi*time_array)

fft_result = fft(signal)

amp = np.abs(fft_result / N)

freq = fftfreq(N, dT)

print(2*amp[np.round(freq,2)==f1])
print(2*amp[np.round(freq,2)==f2])
print(2*amp[np.round(freq,2)==f3])

import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import cycler
colors = ['#000000', '#404040', '#808080', '#C0C0C0', '#FFFFFF']

with mpl.rc_context({'lines.linewidth': 2,
                     'lines.linestyle': '-',
                     'font.family': 'Meiryo',
                     'font.size': 15,
                     'axes.spines.left': True,
                     'axes.spines.bottom': True,
                     'axes.spines.top': False,
                     'axes.spines.right': False,
                     'axes.prop_cycle': cycler(color=colors),
                     'axes.xmargin': 0,
                     'axes.ymargin': 0,
                     'axes.autolimit_mode': 'round_numbers',
                     'xtick.top': False,
                     'xtick.bottom': False,
                     'ytick.left': False,
                     'ytick.right': False,   
                     'figure.autolayout': True,
                     'figure.constrained_layout.use': False,
                     'figure.figsize': (6,4),
                     }):
    fig = plt.figure()
    ax = fig.add_subplot()
    ax.plot(time_array, signal)
    ax.set_aspect('auto')
    plt.xlabel('Time[s]')
    plt.ylabel('Amplitude') 
    plt.xlim(0, max(time_array))
    plt.yticks([-3, -2, -1, 0, 1, 2, 3],
                ['-3.0', '-2.0', '-1.0', '            0', '1.0', '2.0', '3.0'])
    plt.show()

    fig = plt.figure()
    ax = fig.add_subplot()
    ax.plot(freq[0:N//2], 2*amp[0:N//2])
    ax.set_aspect('auto')
    plt.xlabel('Frequency[Hz]')
    plt.ylabel('Amplitude')
    plt.xlim(0, max(freq[0:N//2]))
    plt.yticks([0, 0.5, 1, 1.5],
                ['            0', '0.5', '1.0', '1.5'])
    plt.show()

0603_7a.png
0603_7b.png

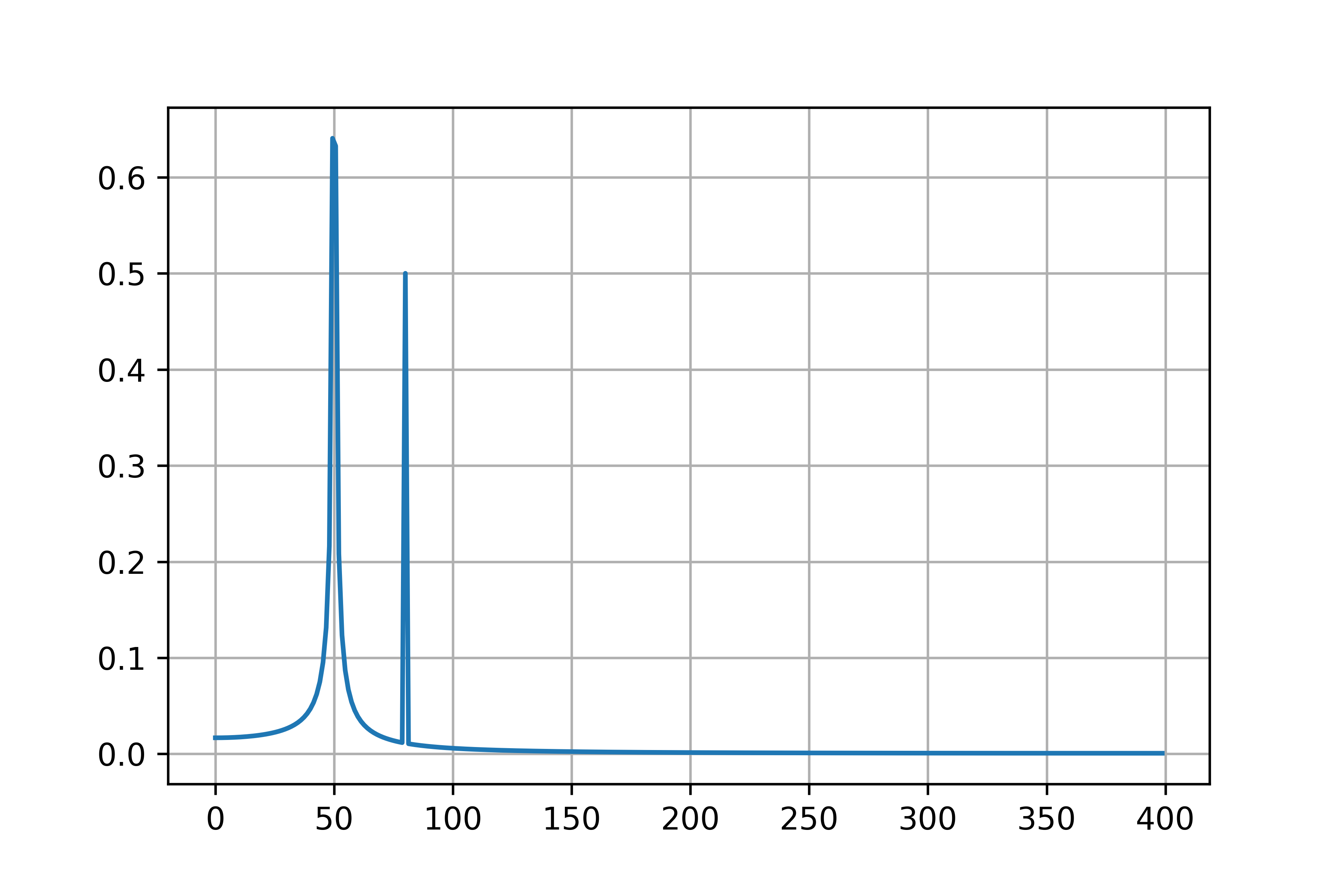
画像が生成されました，うれしいですね．

プリントされた結果から，正しく，

周波数（Hz） 1.00 2.00 2.01
振幅 1.00 0.50 1.00

となっていることがわかるはずです．
信号長を100秒にして周波数分解能を0.01Hzにすることで，
正しく2.01Hzの信号を計測することができました．

常に信号長を長くすることができるのか．

しかし，上記の解決策では不満に思う方も多いでしょう．
0.01秒しか計測することがそもそも不可能な信号は，
必ず，周波数分解能が必ず10Hzになってしまう！

そんな方のためにZero Padding1という手法が存在します．

信号の最後に0を付け加えることによって，仮想的に信号長を長くするのです．

最後に．

二日間だけと決めていましたが，楽しかったので，またいつか続きを書くかもです！
次の記事でお会いしましょう！
失礼します．

  1. Zero Padding Applications - MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT) WITH AUDIO APPLICATIONS SECOND EDITION ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0