はじめに.
FFTをする際は,
Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manual
にある,以下のコードを実行することが多いかもしれません.
from scipy.fft import fft, fftfreq
import numpy as np
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = fftfreq(N, T)[:N//2]
import matplotlib.pyplot as plt
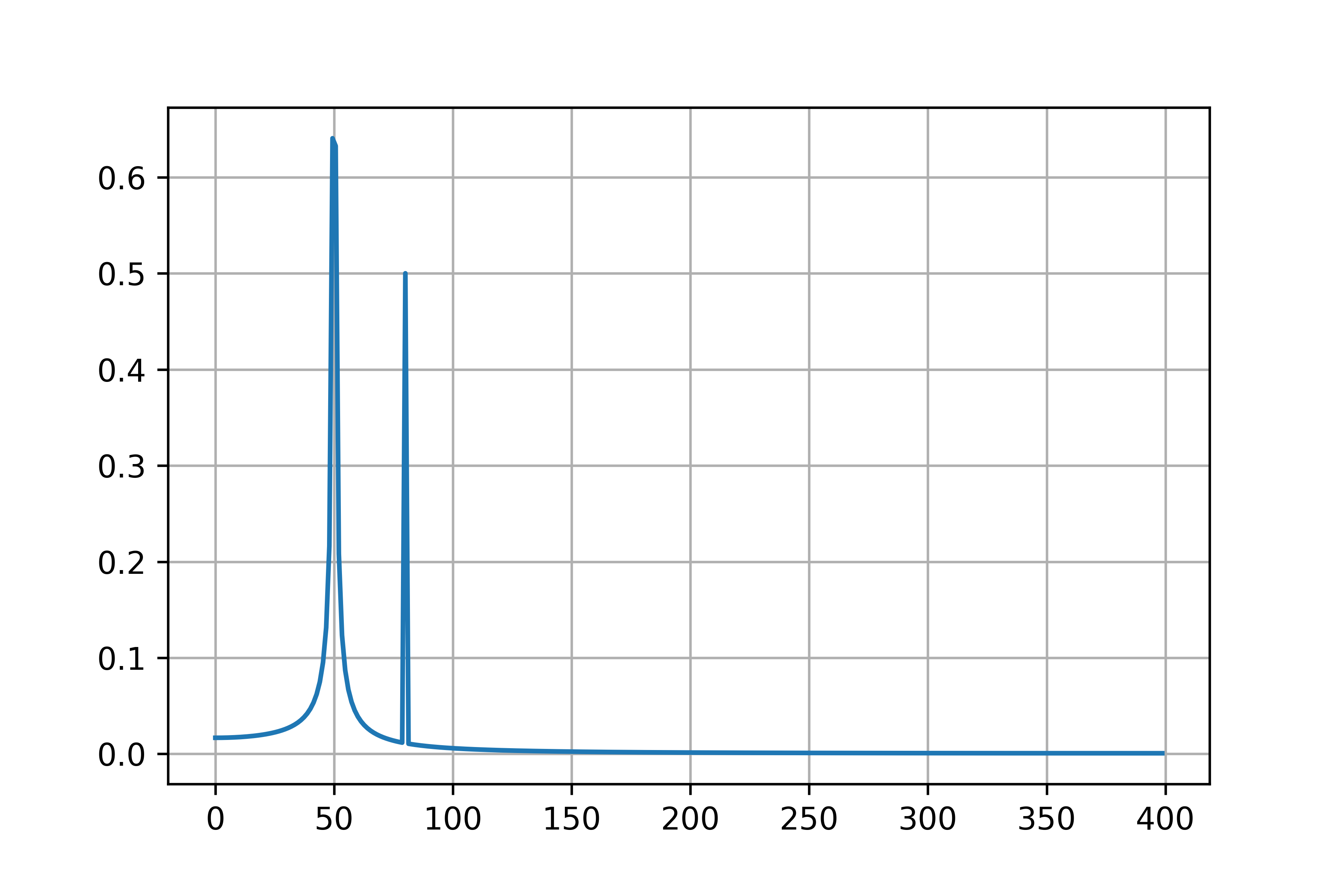
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()
このコードを見たときにいくつか不思議に思う点があると思います.
- なぜ
[0:N//2]でスライスしているの? - なぜ
2.0/N * np.abs(yf[0:N//2])と表示しているの? - 本当にIFFTで元の信号の戻るの?
- 振幅スペクトル,位相スペクトルやパワースペクトルとの違いはなに?
- 振幅が1になってないのはなぜ?
前回の記事では,
「なぜ[0:N//2]でスライスしているの?」
という疑問に対して私なりの結論を提示させていただきました.
具体的には,
一般にフーリエ変換の結果を示す際は対称性から正の周波数成分のみで良い.
という理由から,スライスが実行されていました.
今回は,
「なぜ2.0/N * np.abs(yf[0:N//2])と表示しているの?」
という疑問を解消したいと思います.
この疑問は二つの疑問に分割可能だと考えております.
- なぜフーリエ変換の結果に2をかけているの?
- なぜフーリエ変換の結果を要素数で割っているの?
それぞれの疑問に対して私なりの回答を示せればと思っております.
ちなみにこの記事は論文執筆の気分転換に書いているものなのでどこまで続くかは不明です.
要素数で割る理由.
この疑問に答える際に,皆様に問わなければならないことがあります.
それは,
あなたはフーリエ変換を通して何を知りたいですか?OR求めたいですか?
という質問です.
不快に感じられたら申し訳ないですが,それが本当に重要なので,
問わせていただきました.
例えば問題に(教授,講師,上司が),振幅スペクトルもしくは,位相スペクトルもしくは,
パワースペクトル,パワースペクトル密度を求めよということを記載(発言)されていると思います.
あなたは何を求めたいのか,それが重要なのです!
では,まず最初に結論からですが,2.0/N * np.abs(yf[0:N//2])は,scipy.fftにおいて,
振幅スペクトルを求める計算です.
離散フーリエ変換の定義.
プログラムでは離散信号$x(t)$に対してフーリエ変換を扱います.
そのようなフーリエ変換を離散フーリエ変換と呼びます.
また,プログラム(モジュール)によって,離散フーリエ変換の定義は異なります.
今回は,scipy.fftを基準に考えてみましょう.
離散信号$x(t)$に対して,離散フーリエ変換を,
\begin{align}
\mathrm{X}[k] = \sum_{n~=~0}^{N-1} x[n] e^{-j 2 \pi \frac{kn}{N}}
\end{align}
逆変換を,
\begin{align}
x[n] = \frac{1}{N} \sum_{k~=~0}^{N-1} \mathrm{X}[k] e^{j 2 \pi \frac{kn}{N}}
\end{align}
と定義します.
パワースペクトルとは.
信号処理におけるパワーとは二乗平均値のことです.1
つまり,定義に従うと,
\begin{align}
\mathrm{POWER} &= \frac{1}{N} \sum_{n~=~0}^{N-1} |x[n]|^2 \\
&= \frac{1}{N} \sum_{n~=~0}^{N-1} | \frac{1}{N} \sum_{k~=~0}^{N-1} \mathrm{X}[k] e^{j 2 \pi \frac{kn}{N}} |^2 \\
&= \frac{1}{N} \sum_{n~=~0}^{N-1} | \frac{1}{N} \sum_{k~=~0}^{N-1} \mathrm{X}[k] |^2 \\
&= \frac{1}{N} \sum_{n~=~0}^{N-1} \sum_{k~=~0}^{N-1} \left| \frac{\mathrm{X}[k]}{N} \right| ^2 \\
&= \frac{1}{N} N \sum_{k~=~0}^{N-1} \left| \frac{\mathrm{X}[k]}{N} \right| ^2 \\
&= \sum_{k~=~0}^{N-1} \left| \frac{\mathrm{X}[k]}{N} \right| ^2 \\
\end{align}
そして,パワースペクトルとは,それぞれの周波数帯にどれだけのパワーが存在するか示すものです.
つまり,scipy.fftで,パワースペクトルは
\begin{align}
\mathrm{POWER(k)} &= \left| \frac{\mathrm{X}[k]}{N} \right| ^2 \\
&= np.power( np.abs( \frac{\text{フーリエ変換の結果}}{\text{要素数}} ) ,2)
\end{align}
であることが分かりました.
振幅スペクトルとは.
振幅スペクトルとは,それぞれの周波数帯にどれだけの振幅が存在するか示すものです.
その定義から,複素フーリエ級数の絶対値であることが分かります.
連続信号$x(t)$に対して,複素フーリエ級数$c_n$
\begin{align}
c_n &= \frac{1}{T} \int_{0}^{T} x(t) e^{-jn\omega t} dt
\end{align}
を定義したとき,複素フーリエ級数展開は,
\begin{align}
x(t) = \sum_{n~=~-\infty}^{\infty} c_n e^{jn\omega t} \\
\end{align}
と定義されます.
ここで,信号処理におけるパワーとは二乗平均値のことなので1,
連続信号$x(t)$に対して,区間$[ 0 , T ]$におけるパワーは,
\begin{align}
\mathrm{POWER} &= \frac{1}{T} \int_{0}^{T} |x[n]|^2 \\
&= \frac{1}{T} \int_{0}^{T} |\sum_{n~=~-\infty}^{\infty} c_n e^{jn\omega t}|^2 \\
&= \frac{1}{T} \int_{0}^{T} \sum_{n~=~-\infty}^{\infty} | c_n |^2 \\
&= \frac{1}{T} T \sum_{n~=~-\infty}^{\infty} | c_n |^2 \\
&= \sum_{n~=~-\infty}^{\infty} | c_n |^2 \\
\end{align}
つまり,
\begin{align}
\sum_{k~=~0}^{N-1} \left| \frac{\mathrm{X}[k]}{N} \right| ^2 = \sum_{n~=~-\infty}^{\infty} | c_n |^2
\end{align}
であり,十分なサンプリング周波数を確保し,標本化定理を満たすとき,
離散信号$x(t)$から連続信号$x(t)$へ変換可能なので,
上記式を一対一で満たす,$k$と$n$の組は存在します.
よって,scipy.fftで,振幅スペクトルは
\begin{align}
\mathrm{AMPLITUDE(k)} &= \left| \frac{\mathrm{X}[k]}{N} \right| \\
&= np.abs( \frac{\text{フーリエ変換の結果}}{\text{要素数}} )
\end{align}
であることが分かりました.
例えば,
from scipy.fft import fft, ifft, fftfreq
import numpy as np
T = 4
fs = 8
f1 = 1
f2 = 2
N = int(fs * T)
dT = 1.0 / fs
time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array) + 0.5*np.sin(f2 * 2.0*np.pi*time_array)
fft_result = fft(signal)
print( np.sum( np.power(np.abs(fft_result / N),2) ) )
print( np.sum(np.power(np.abs(signal),2) / N) )
を実行してみると,どちらも0.625となり,同じ値であることがわかります.
2をかける理由.
前回の記事で,
一般にフーリエ変換の結果を示す際は対称性から正の周波数成分のみで良い.
ことがわかりました.
ここで,片側スペクトルのみを表示する場合,
振幅スペクトルの二乗値の合計がパワーとならないと元の信号に戻らないため,二倍されています.
振幅スペクトルを表示する.
例えば,以下のようなコードを実行してみましょう.
from scipy.fft import fft, ifft, fftfreq
import numpy as np
T = 4
fs = 8
f1 = 1
f2 = 2
N = int(fs * T)
dT = 1.0 / fs
time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array) + 0.5*np.sin(f2 * 2.0*np.pi*time_array)
fft_result = fft(signal)
freq = fftfreq(N, dT)
import matplotlib.pyplot as plt
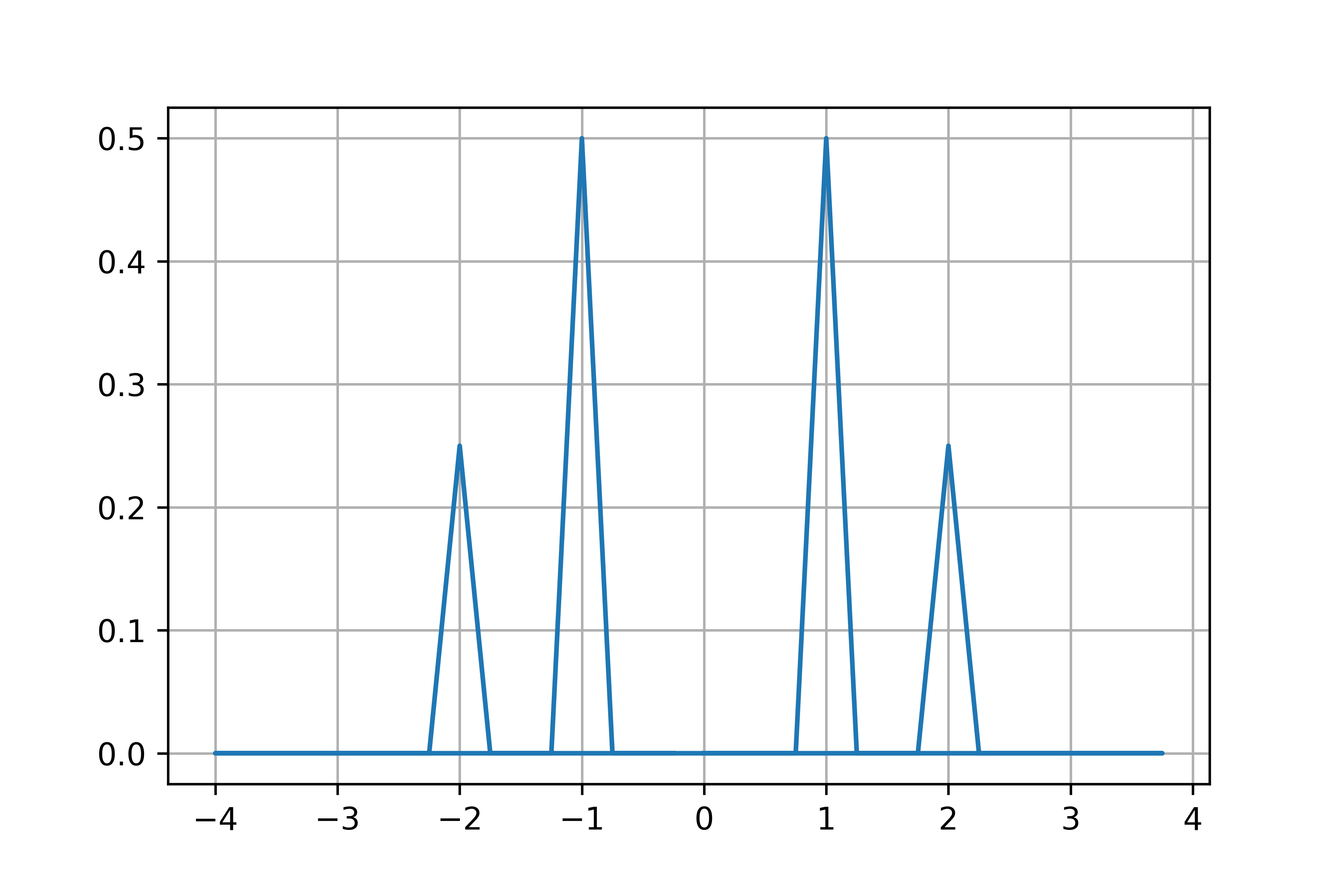
plt.plot(freq, np.abs(fft_result / N))
plt.grid()
plt.show()
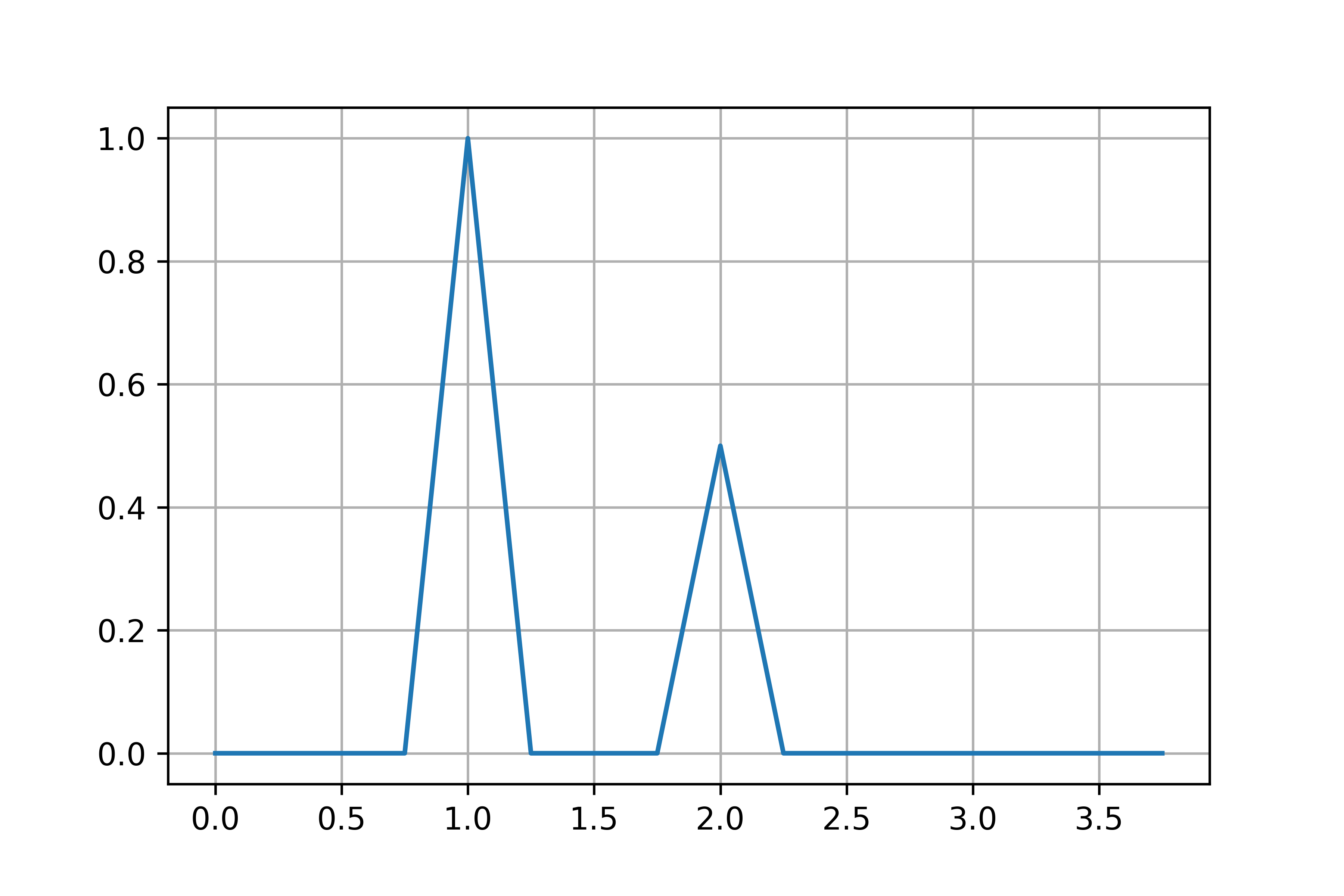
plt.plot(freq[0:N//2], 2*np.abs(fft_result / N)[0:N//2])
plt.grid()
plt.show()
画像が生成されました,うれしいですね.
上画像が,両側の振幅スペクトルであり,下画像が片側の振幅スペクトルです.
一般的にスペクトルは合計値がパワーになることを前提に作られていると思います.
(分野によって諸説はありますが.)
また,前回の記事の結論から,
振幅スペクトルを求めよ,と言われた際は基本的には片側スペクトルを提出すれば良いのではないかと思います.
最後に.
ですます調になってない部分もあるかもしれません.
次の記事でお会いしましょう!
失礼します.