はじめに.
FFTをする際は,
Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manual
というコードを参照されると思いますが,
様々な疑問が生じると思います.
2日間でどこまで書けるか分かりませんが,気分転換にいろいろ書きたいと思います.
FFTをしてみる.
Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manual
のコードを参照します.
from scipy.fft import fft, fftfreq
import numpy as np
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
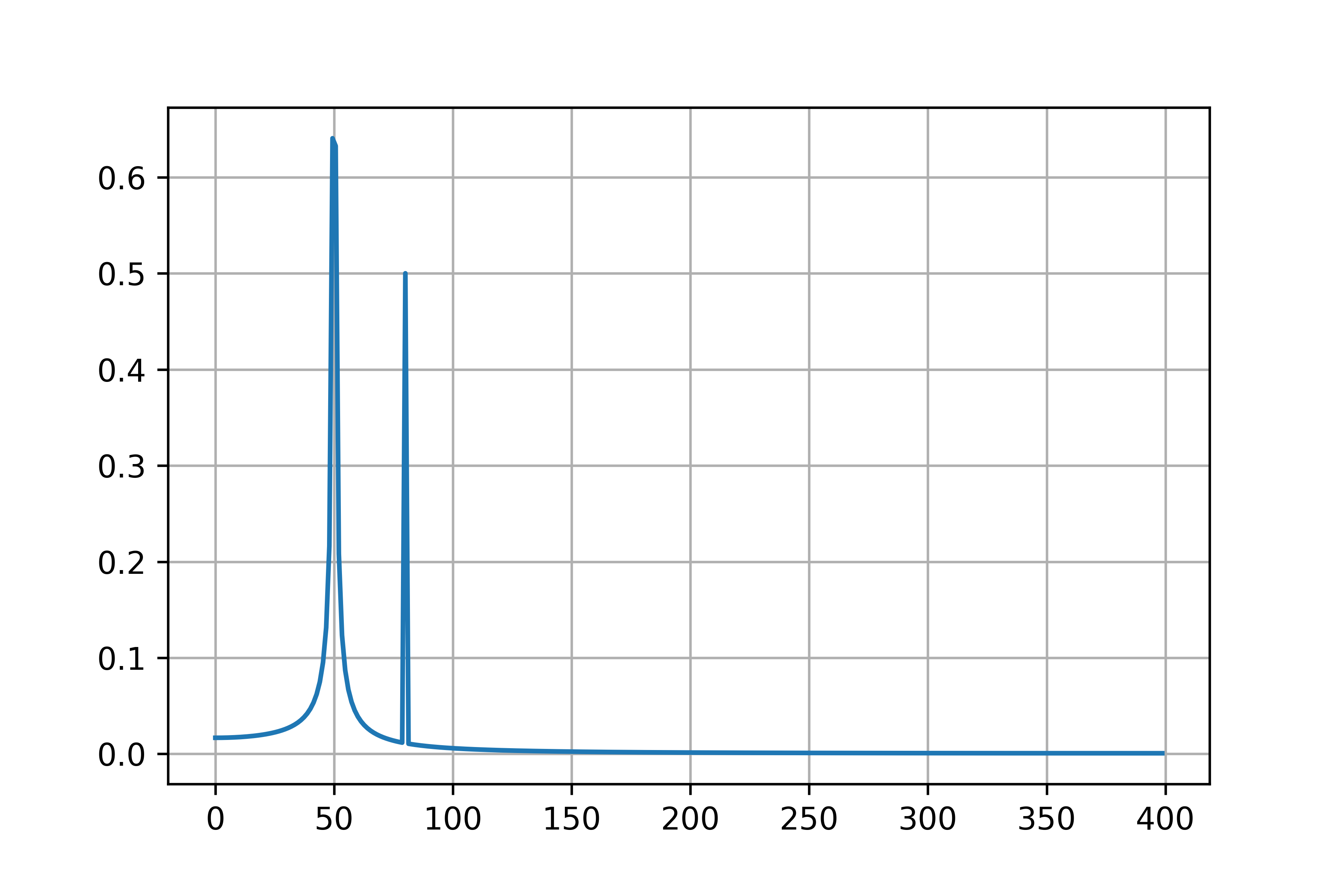
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = fftfreq(N, T)[:N//2]
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()
画像が生成されました,うれしいですね.
このコードを見たときに2点不思議に思う点があると思います.
- なぜ
[0:N//2]でスライスしているの? - なぜ
2.0/N * np.abs(yf[0:N//2])と表示しているの?
詳しい人であれば,
- 本当にIFFTで元の信号の戻るの?
- 振幅スペクトル,位相スペクトルやパワースペクトルとの違いはなに?
という疑問を持ちながら,この記事を読んでいる人もいるかもしれません.
注意深く画像を見ると,
- 振幅が1になってないのはなぜ?
という疑問も出てくると思います.
上記の疑問に対して少しでも解決になればと思い,記事を執筆しました.
サンプリング周波数を導入する.
それぞれコードを解釈しながら,少しづつコードを変更してみましょう.
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
この二つは,サンプル点数とサンプル点の間隔を決めていますね.
一般的に信号時間(信号長)とサンプリング周波数からこれら二つを導出できるので,
少し変更してみましょう.
# Total duration of the signal (in seconds)
T = 6/8
# Sampling frequency (in Hz)
fs = 800
# Number of sample points
N = int(fs * T)
# sample spacing
dT = 1.0 / fs
と変更しましょう.これは6/8秒,サンプリング周波数が800Hzの信号という意味です.
サンプリング周波数は1秒間に何回信号をサンプルしたかという意味なので,
サンプル点数は,$fs \times T$で表せます.
同様に,どれぐらいのサンプル間隔かはサンプリング周波数の逆数で表現できます.
IFFTを試してみる.
例えば,以下のようなコードを実行してみましょう.
from scipy.fft import fft, ifft, fftfreq
import numpy as np
T = 4
fs = 8
f1 = 1
f2 = 2
N = int(fs * T)
dT = 1.0 / fs
time_array = np.linspace(0.0, N*dT, N, endpoint=False)
signal = np.sin(f1 * 2.0*np.pi*time_array) + 0.5*np.sin(f2 * 2.0*np.pi*time_array)
fft_result = fft(signal)
r_signal = ifft(fft_result)
freq = fftfreq(N, dT)
import matplotlib.pyplot as plt
plt.plot(freq, np.abs(fft_result))
plt.grid()
plt.show()
plt.plot(time_array, signal)
plt.grid()
plt.show()
plt.plot(time_array, r_signal.real)
plt.grid()
plt.show()
print(np.round(signal,5) == np.round(r_signal.real,5))
たくさん画像が生成されました,うれしいですね.
コードを解釈する.
このコードは先程のコードと少し変更した点があります.
定義した値の変更.
このコードでは,時間が4秒,サンプリング周波数が8Hz.
また,生成した信号は1Hzと2Hzの信号です.
スライスの廃止.
スライスをするのは不思議ですよね,一度,スライスをやめてみましょう.
IFFTの実行.
FFTを行った値に,IFFT関数を実行すると,元の信号が復元できましたね.
print(np.round(signal, 5) == np.round(r_signal.real, 5))でも,
[ True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True]
と表示され,同一の値であることが確認できたと思います.
コードの解釈.
定義の部分.
4秒,サンプリング周波数が8Hzの信号です.
また,1Hzと2Hzの信号を組み合わせています,それぞれ,振幅は1と0.5です.
スライスをする理由.
一枚目の画像をよく見ると,0に対して対称であるように感じませんか?
Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manual
にもそのような記述がありますね.
For N even, the elements $y[1] \dots y[N/2-1]$
contain the positive-frequency terms, and the elements $y[N/2] \dots y[N-1]$
contain the negative-frequency terms, in order of decreasingly negative frequency.
For N odd, the elements $y[1] \dots y[(N-1)/2]$
contain the positive-frequency terms, and the elements $y[(N+1)/2] \dots y[N-1]$
contain the negative-frequency terms, in order of decreasingly negative frequency.
Nが偶数の場合,要素$y[1] \dots y[N/2-1]$には正の周波数項が含まれ,
要素$y[N/2] \dots y[N-1]$には負の周波数項が含まれます.
負の周波数項は,負の周波数の減少順に並んでいます.
Nが奇数の場合,要素$y[1] \dots y[(N-1)/2]$には正の周波数項が含まれ,
要素$y[(N+1)/2] \dots y[N-1]$には負の周波数項が含まれます.
負の周波数項は,負の周波数の減少順に並んでいます.
ただこの記述だけでは,本当に対称かは分かりません,
数学的に示してみましょう.
対称性の説明.
$y(t)\in \mathbb{R}$をフーリエ変換した際の,結果を$\mathcal{F}[y(t)]=\mathrm{Y}(\omega)$とします.
ここで,$\mathcal{F}[y(t)]=\mathrm{Y}(\omega)=\mathrm{Re}(\omega)-i\mathrm{Im}(\omega)$と表現できるとします.$y(t)\in \mathbb{R}$なので,$\omega>0$について
\begin{align}
\mathrm{Re}(\omega) &= \int_{-\infty}^{\infty} y(t) \cos(\omega t) dt \\
\mathrm{Im}(\omega) &= \int_{-\infty}^{\infty} y(t) \sin(\omega t) dt
\end{align}
となります.ここで,
\begin{align}
\mathrm{Re}(-\omega) &= \int_{-\infty}^{\infty} y(t) \cos(-\omega t) dt = \int_{-\infty}^{\infty} y(t) \cos(\omega t) dt = \mathrm{Re}(\omega) \\
\mathrm{Im}(-\omega) &= \int_{-\infty}^{\infty} y(t) \sin(-\omega t) dt = -\int_{-\infty}^{\infty} y(t) \sin(\omega t) dt = - \mathrm{Im}(\omega)
\end{align}
よって,
\mathrm{Y}(-\omega)=\mathrm{Re}(-\omega)-i\mathrm{Im}(-\omega)=\mathrm{Re}(\omega)+i\mathrm{Im}(\omega)=\overline{\mathrm{Y}(\omega)}
また,
\mathrm{ABSOLUTE}(\mathrm{Y}(-\omega)) = \sqrt{ \mathrm{Re^2}(\omega) + \mathrm{Im^2}(\omega) } = \mathrm{ABSOLUTE}(\mathrm{Y}(\omega))
ただし,
\mathrm{Y}(0) = \int_{-\infty}^{\infty} y(t) e^{j0 t}dt = \int_{-\infty}^{\infty} y(t)dt
なので,$y(t)\in \mathbb{R}$をフーリエ変換した際,フーリエ変換の結果は$0Hz$を除いて正負で対称であることがわかります.
フーリエ変換の結果は0Hzを除いて正負で対称である.
ついでに,フーリエ変換周りの重要な定理に関して一つ証明をしたいと思います.
パーシバルの定理(Rayleigh Energy Theorem / Parseval's Theorem)の説明.
フーリエ変換を
\begin{align}
\mathrm{X}(\omega) = \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt
\end{align}
逆変換を,
\begin{align}
x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{X}(\omega) e^{j\omega t} d\omega
\end{align}
と定義したとしましょう.
(Fourier Transforms (scipy.fft) — SciPy v1.10.1 Manualにおける定義と本質は同じです.)
ここで,$x(t)\in \mathbb{R}$に対して,
\begin{align}
\int_{-\infty}^{\infty} |x(t)|^2 dt &= \int_{-\infty}^{\infty} x(t) x(t) dt \\
&= \int_{-\infty}^{\infty} x(t) \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{X}(\omega) e^{j\omega t} d\omega dt \\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{X}(\omega) \int_{-\infty}^{\infty} x(t) e^{j\omega t} dt d\omega \\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{X}(\omega) \mathrm{X}(-\omega) d\omega \\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{X}(\omega) \overline{\mathrm{X}(\omega)} d\omega \\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} | \mathrm{X}(\omega) |^2 d\omega \\
\end{align}
フーリエ変換対$x(t)$,$\mathrm{X}(\omega)$に対して,
\int_{-\infty}^{\infty} |x(t)|^2 dt = \frac{1}{2\pi} \int_{-\infty}^{\infty} | \mathrm{X}(\omega) |^2 d\omega
が成立する.このことをパーセバルの定理と呼ぶ.
真・スライスをする理由.
パーセバルの定理の証明が挟まり,若干脱線してしまいましたね.
失礼しました.
気を取り直して,スライスをする理由としては,
フーリエ変換の結果は対称性を持っているためスライスをしている.
というのが回答になるのではないでしょうか.
つまり見やすさですね.
ここからは個人的な感想を箇条書きにします.一種のお気持ち表明です.
- フーリエ変換は負の周波数まで定義されている.
- グラフなどで表示した際,負の周波数は理解しずらい.
- 負の周波数の結果と正の周波数の結果は同じである.
という思考の結果,
一般的に負の周波数を除いた,正の周波数のみが表示されているのではないかと思います.
一般にフーリエ変換の結果を示す際は対称性から正の周波数成分のみで良い.
最後に.
少し長くなったので次の記事でお会いしましょう!
失礼します.