More than 5 years have passed since last update.

ロジスティック回帰に対するFeature Hashingの影響

Posted at 2019-07-28

はじめに

AI.RL.LYsのtyoshitakeです。
今回はカテゴリカル変数を含んだデータに対してロジスティック回帰を行う際にFeature Hashingを用いた場合、ロジスティック回帰の性能にどのような影響を及ぼすかを調べました。

Feature Hashingとは

解析対象データがカテゴリカル変数を含む場合、解析しやすいように数値的な表現に変換する必要があります。その際によく用いられるのがone-hotエンコーディングやダミーコーディングなどです。¹
例えば以下の表のように社員データの特徴量ベクトルはone-hotエンコーディングすると下の式のようになります。

	職種	趣味
社員A	営業	釣り
社員B	デザイナー	サッカー
社員C	エンジニア	盆栽

社員A = \left( \begin{matrix} 職種＿営業 \\ 職種＿デザイナー \\ 職種＿エンジニア \\ 趣味＿釣り \\ 趣味＿サッカー \\ 趣味＿盆栽 \end{matrix} \right)
= \left( \begin{matrix} 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{matrix}\right),\quad
社員B=\left( \begin{matrix} 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{matrix}\right),\quad
社員C=\left( \begin{matrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{matrix}\right)

カテゴリ変数のカテゴリーの種類がN種類の場合、one-hotエンコーディングするとある１つの成分のみが1で他が0のN次元ベクトルとなります。したがってカテゴリ変数のカテゴリー数が非常に多い場合、特徴量ベクトルは成分の殆どが0となる、疎(スパース)なベクトルとなります。²この表現ベクトルは重要な情報(1)に対して余分な情報(0)が多く、また計算上も大きなメモリ領域をとってしまう³ので扱いづらいです。

Feature Hashingではハッシュ関数を用いてカテゴリカル変数データを指定した次元のベクトルに圧縮します。
例えば社員Aのデータを{"職種": "営業", "趣味": "釣り"}と表現します。Feature Hashingの指定次元を$m$、ハッシュ関数を$hash$、符号に関するハッシュ関数を$hash_s$、Feature Hashing後の$m$次元特徴量ベクトルを$\boldsymbol{x_A}$とすると社員Aデータに対するFeature Hashingの処理は以下のようになります。

Feature Hashing

特徴量ベクトル$\boldsymbol{x_A}$の各成分を0で初期化する。
ハッシュ値 $h=hash("職種":"営業")$ を計算する。
符号ハッシュ値 $h_{s}=hash_s("職種":"営業")$ を計算する。
$i = mod(h, m)$
$mod(h_s, 2) = 0$ なら $\boldsymbol{x_A}[i] += 1$
$mod(h_s, 2) = 1$ なら $\boldsymbol{x_A}[i] += -1$
2-4を**"趣味":"釣り"**についても計算する。

以上の処理⁴によってデータを指定した次元の特徴量ベクトルで表現できます。
Feature Hashingではデータをハッシュ関数で処理しても、それによって大きなバイアスが生じないことがわかっています。⁵

実験

実際にFeature Hashingを用いて次元の削減を行った場合にロジスティック回帰によるクラス分類の精度がどのように変化するかを調べてみます。

開発環境

python 3.6.5
numpy 1.16.4
pandas 0.24.2
scikit-learn 0.21.2
matplotlib 3.1.1

開発・実行はjupyter notebookで行っています。

データセット

データセットはアメリカの成人の収入と種々の因子との関連について調べた国勢調査データを用いました。
https://www.kaggle.com/johnolafenwa/us-census-data

データセットにはおよそ3万件のデータが有り、各データの属性(カラム名)は以下のようになっています。

カラム名	内容	取りうる値の数
age	年齢
workclass	雇用形態	9
fnlwgt	統計処理に用いる重み
education	学歴	16
education.num	学歴(数値表現)	16
marital.status	結婚の有無・状態	7
occupation	職業	15
relationship	家庭内の立場	6
race	人種	5
sex	性別	2
capital.gein	キャピタルゲイン
capital.loss	キャピタルロス
hours.per.week	１週間辺りの労働時間
native.country	出身国	42
income	収入	2

カテゴリ変数のみ取りうる値の数を記載しています。

以下では、年収が５万ドル以上か以下かの2クラスに分類するクラス分類問題に対してロジスティック回帰を用いて学習・予測を行い、予測精度に対する次元削減の影響を調べました。

データの前処理

データの前処理として以下を行います。

"fnlwgt"は予測には関係ない因子なので除外
"education.num"は"education"と同じ内容なので除外
"age", "capital.gain", "capital.loss", "hours.per.week"は10個程度のビンで量子化する
予測変数"income"の数値化(5万ドル超え: 1, 5万ドル以下: 0)

数値変数の量子化は必ずしも行う必要はありませんが、今回扱うデータの変数をすべてカテゴリカル変数にするために行っています。

以下がデータの前処理のコードです。

import pandas as pd
import numpy as np

# データの読み込み
data = pd.read_csv('path/to/data')

# 不要な項目を除く
data = data.drop(columns=['education.num', 'fnlwgt'])

# 数値変数の量子化
# age
bins_age = np.linspace(10, 90, 9)
data['age'] = np.digitize(data['age'], bins=bins_age)

# capital.gain
bins_cg = np.linspace(0, 100000, 11)
data['capital.gain'] = np.digitize(data['capital.gain'], bins=bins_cg)

# capital.loss
bins_cl = np.linspace(0, 5000, 11)
data['capital.loss'] = np.digitize(data['capital.loss'], bins=bins_cl)

# hours.per.week
bins_hpw = np.linspace(0, 100, 11)
data['hours.per.week'] = np.digitize(data['hours.per.week'], bins=bins_hpw)

# 予測変数の数値化
data['income'] = (data['income'] == '>50K').astype(int)

# 数値を文字列化
column_names = ['age', 'capital.gain', 'capital.loss', 'hours.per.week']
for column_name in column_names:
    data[column_name] = data[column_name].astype('str')

最後の文字列化の処理はscikit-learnでFeature Hashingを行うための処理です(後述)。

One-Hotエンコーディングに対する結果

まず比較の基準としてOne-Hotエンコーディングしたデータに対しロジスティック回帰を行っています。
ロジスティック回帰は正則化パラメータを変えて行い、精度の正則化パラメータ依存性をグラフとして出力しています。

コードは以下です。

import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# one-hotエンコーディング
dummy_columns = list(data.columns)
dummy_columns.remove('income')
data_oh = pd.get_dummies(data, columns=dummy_columns, sparse=True)

X = data_oh.drop(columns='income')
y = data_oh['income']

# 訓練データとテストデータに分割(訓練データ: 75%, テストデータ: 25%)
random_state = 4
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=random_state, test_size=0.25)

# 正則化定数を変えて精度を記録
reg_params = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
training_acc = []
test_acc = []

for reg_param in reg_params:
    
    # 線形ロジスティック回帰モデルを作成
    clf = LogisticRegression(random_state=random_state, solver='lbfgs', C=reg_param, max_iter=1000, fit_intercept=False).fit(X_train, y_train)
    
    # 訓練セット精度を記録
    training_acc.append(clf.score(X_train, y_train))
        
    # 汎化精度を記録
    test_acc.append(clf.score(X_test, y_test))
    
# 精度の正則化定数依存性を図示
plt.plot(reg_params, training_acc, label="training accuracy")
plt.plot(reg_params, test_acc, label="test accufacy")
ax = plt.gca()
ax.set_xscale('log')
plt.ylabel("Accuracy")
plt.xlabel("Reguralization parameter")
plt.legend()

結果は以下の図のようになりました。

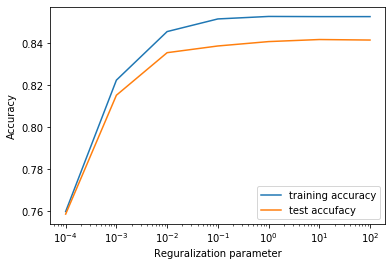
グラフ横軸が正則化パラメータの逆数でグラフ縦軸が精度です。グラフ上には訓練データとテストデータに対する結果をプロットしています。
グラフ上を左に行くほど正則化が強くパラメータの自由度が小さくなっており、右に行くほど正則化が弱くパラメータの自由度が高くなっています。
図より、テストデータに対する精度は0.835程度であることがわかります。
ちなみにone-hotエンコーディングした特徴量ベクトルのサイズは137次元となりました。

Feature Hashingによる影響

次にFeature Hashingにより特徴量ベクトルの次元削減を行った場合、先程の精度がどのように変化するかを調べました。特徴量ベクトルのサイズはone-hotエンコーディング時の特徴量ベクトル次元が137であることを考慮して、2~130の間で振っています。
Feature Hashingはscikit-learnのFeatureHasherを用いています。
https://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.FeatureHasher.html
コードは以下です。

from sklearn.feature_extraction import FeatureHasher

dims = [2, 5, 10, 20, 30, 40, 50, 100, 130]
reg_params = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0]

# グラフ設定
fig, axes = plt.subplots(3, 3, figsize=(20, 14))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
plt.rcParams["font.size"] = 14

# データ
X = data.drop(columns='income')
y = data['income']

# 訓練データとテストデータに分割(訓練データ: 75%, テストデータ: 25%)
random_state = 4
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=random_state, test_size=0.25)

# FeatureHasherで処理するためにデータを辞書化する
X_train_dict = [X_train.iloc[i_row].to_dict() for i_row in range(len(X_train))]
X_test_dict = [X_test.iloc[i_row].to_dict() for i_row in range(len(X_test))]

for dim, ax in zip(dims, axes.reshape(-1)):
    
    # Feature Hashing
    fh = FeatureHasher(n_features=dim)
    X_fh_train = fh.fit_transform(X_train_dict).toarray()
    X_fh_test = fh.fit_transform(X_test_dict).toarray()
    y_fh_train = y_train
    y_fh_test = y_test
    
    # 精度格納変数の初期化
    training_acc = []
    test_acc = []
    
    # 各正則化定数で線形ロジスティック回帰を実行
    for reg_param in reg_params:

        # 線形ロジスティック回帰モデルを作成
        clf = LogisticRegression(random_state=random_state, solver='lbfgs', C=reg_param, max_iter=1000, fit_intercept=False).fit(X_fh_train, y_train)

        # 訓練セット精度・汎化精度を記録
        training_acc.append(clf.score(X_fh_train, y_train))
        test_acc.append(clf.score(X_fh_test, y_test))

    # 結果の図示
    ax.plot(reg_params, training_acc, label="training_acc")
    ax.plot(reg_params, test_acc, label="test_acc")
    ax.yaxis.set_major_formatter(plt.FormatStrFormatter('%.2f'))
    ax.set_title("{} features".format(dim))
    ax.set_xscale('log')
    ax.set_ylabel("Accuracy")
    ax.set_xlabel("Reguralization parameter")

axes.reshape(-1)[0].legend()

結果は以下の図のようになりました。

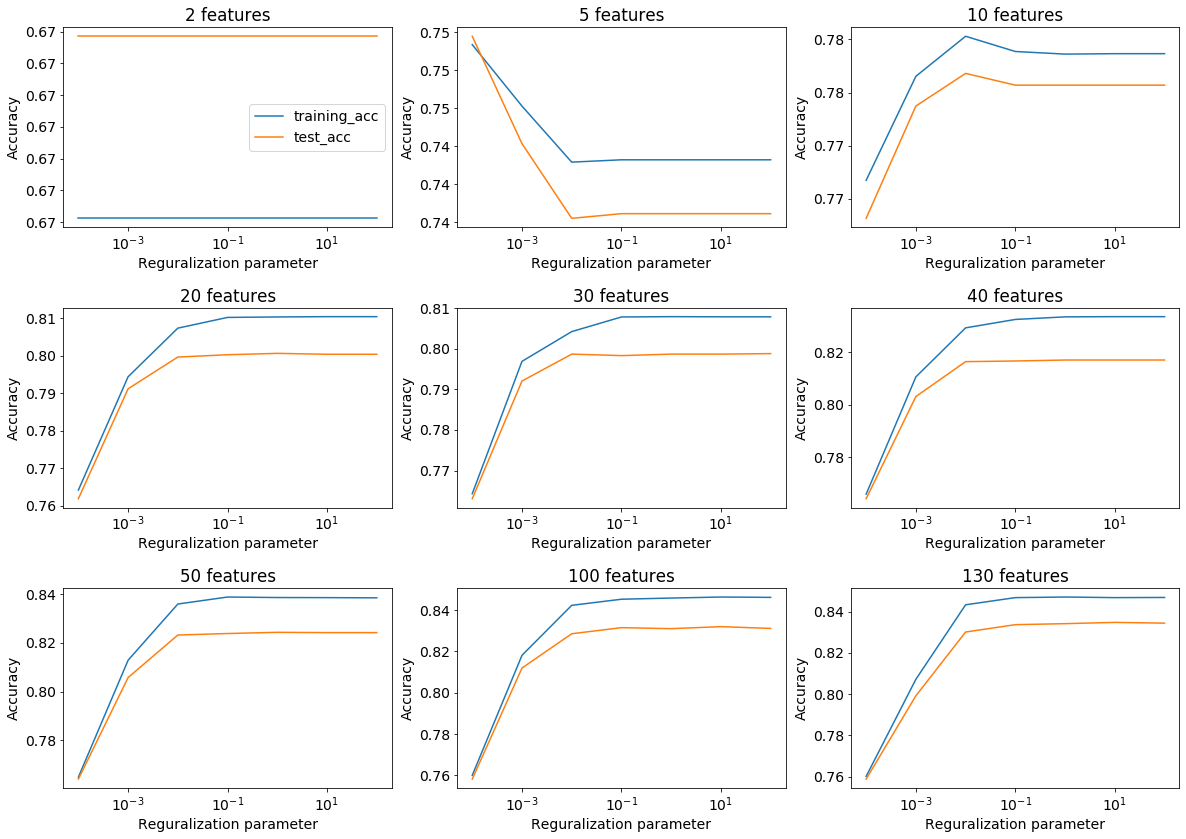
図を見たところ以下のことがわかります。

特徴量ベクトルサイズが40~130ではテストデータに対する精度が0.82~0.83程度
特徴量ベクトルサイズが20~30では40~130にくらべ精度が下がる(0.8程度)
特徴量ベクトルサイズが2~10ではベクトルサイズの減少に応じてテストデータに対する精度が大きく減少する。

one-hotエンコーディングしたデータに対する解析結果(テストデータに対する精度が0.835)と比べるとFeature Hashingにより精度の低下が起きていることがわかります。しかし、特徴量ベクトルサイズが40~130の範囲では次元が1/3程度まで圧縮できているのにも関わらず、それほど精度が低下していません。一般にデータの次元が大きければ大きいほど、線形モデルを用いて分類しやすくなりますが、今回のデータでは40次元ほどあれば十分分類可能であるといえます。
したがって、実際の計算コストによってはFeature Hashingにより次元削減することが有効な手段となりえます。

今回用いたデータセットはカテゴリの種類が最大でも40程度なので、特徴量ベクトルもそこまで疎でなくFeature Hashingによる圧縮率も大きくはありませんでしたが、カテゴリ変数の取りうる値が数百・数千となると圧縮率もより大きくなると期待され、計算コストの増加も相まってFeature Hashingの有効性が高まります。

参考

機械学習のための特徴量エンジニアリングその原理とPythonによる実践
https://www.amazon.co.jp/dp/4873118689
Pythonはじめる機械学習
https://www.amazon.co.jp/dp/4873117984
scikit-learn公式ドキュメント
https://scikit-learn.org/stable/documentation.html

カテゴリ変数のエンコーディングについては以前書いた記事があります。
https://qiita.com/tyoshitake/items/cf244287254b92b0e7c4 ↩
実際には各データの特徴量ベクトルを並べて作成した行列に対して計算処理を行うことが多いので、疎(スパース)な行列と表現されることが多いです。 ↩
注釈2同様計算処理の対象は各データの特徴量ベクトルからなる行列なので、データセット内のデータ数と特徴量ベクトルサイズによっては膨大なメモリ領域が必要になります。 ↩
Feature Hashingの処理の概要の説明であり、実際のの実装内容を考慮していません。今回用いたscikit-learnのFeatureHasherの実装内容については以下のドキュメントを参照してください。
https://scikit-learn.org/stable/modules/feature_extraction.html#feature-hashing ↩
https://alex.smola.org/papers/2009/Weinbergeretal09.pdf ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up