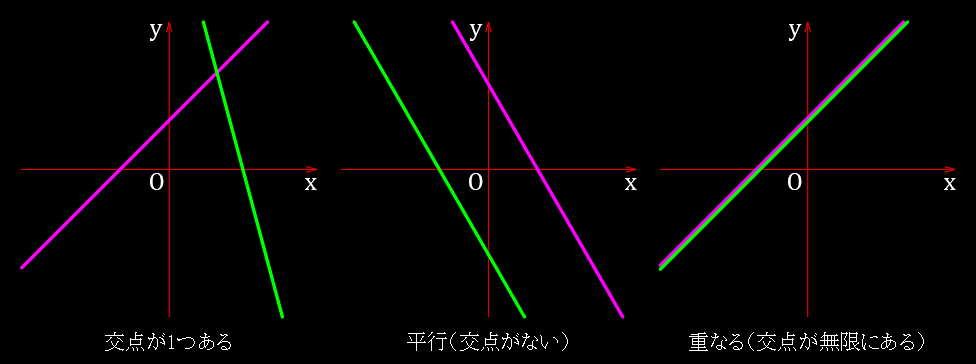
平面上の2直線の位置関係
平面上の2直線の位置関係は、
- 交点がある
- 平行(交点がない)
- 重なる(交点は無限)
のいずれか。
2直線の交点の求め方
直線の方程式一般形の形で表された2直線、
$a_1x+b_1y+c_1=0\ \ \ と\ \ \ a_2x+b_2y+c_2=0$
の交点を求める。

この2直線に交点があると仮定して、その交点を $P(x_0,y_0)$ とすると、
交点 $P$ は2直線両方の上にあるので、2直線の2つの式の連立方程式、
$$\begin{cases}
a_1x+b_1y+c_1=0\ \cdots \ ① \
a_2x+b_2y+c_2=0\ \cdots \ ②
\end{cases}$$
を解くことで求めることができる。
2直線の交点を求める
①② の式の $y$ を消去する。
① の両辺に $b_2$ を、 ② の両辺に $b_1$ を掛けて、
$$\begin{cases}
a_1b_2x+b_1b_2y+b_2c_1=0\ \cdots \ ①' \
a_2b_1x+b_1b_2y+b_1c_2=0\ \cdots \ ②'
\end{cases}$$
①' から ②' を引いて整理すると、
$$(a_1b_2-a_2b_1)x+b_2c_1-b_1c_2=0$$
$$(a_1b_2-a_2b_1)x=(b_1c_2-b_2c_1)\ \cdots \ ③$$
①② の式の $x$ を消去する。
② の両辺に $a_1$ を、① の両辺に $a_2$ を掛けて、
$$\begin{cases}
a_1a_2x+a_1b_2y+a_1c_2=0\ \cdots \ ②'' \
a_1a_2x+a_2b_1y+a_2c_1=0\ \cdots \ ①''
\end{cases}$$
②'' から ①'' を引いて整理すると、
$$(a_1b_2-a_2b_1)y+a_1c_2-a_2c_1=0$$
$$(a_1b_2-a_2b_1)y=(a_2c_1-a_1c_2)\ \cdots \ ④$$
となる。式 ③ ④ より、
$$a_1b_2-a_2b_1\neq0\ \ すなわち\ \ \frac{a_1}{a_2}\neq\frac{b_1}{b_2}$$
であれば、2直線の交点は存在して、その座標は
$$x=\frac{b_1c_2-b_2c_1}{a_1b_2-a_2b_1}\ \ ,\ \ y=\frac{a_2c_1-a_1c_2}{a_1b_2-a_2b_1}$$
となる。また、
$$a_1b_2-a_2b_1=0\ \ かつ\ \ b_1c_2-b_2c_1\neq0\ \ ,\ \ a_2c_1-a_1c_2\neq0$$
すなわち、
$$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$$
の場合、この連立方程式は不能で解は存在しない。
これは、2直線の関係が平行であることを表している。
さらに、
$$a_1b_2-a_2b_1=0\ \ かつ\ \ b_1c_2-b_2c_1=0\ \ ,\ \ a_2c_1-a_1c_2=0$$
すなわち、
$$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$$
ならば、この連立方程式は不定で解は無限に存在する。
これは、2直線の関係がが重なっていることを表している。
2直線、$a_1x+b_1y+c_1=0\ \ \ と\ \ \ a_2x+b_2y+c_2=0$ の交点は、
$$\left(\frac{b_1c_2-b_2c_1}{a_1b_2-a_2b_1}\ \ ,\ \ \frac{a_2c_1-a_1c_2}{a_1b_2-a_2b_1}\right)\ \ \ \ \ \ \ ただし、a_1b_2-a_2b_1\neq0$$
2線分を選択、交点を出力するプログラム
;; 2線分を選択して、交点を出力する
(defun c:SelectTwoLineAndOutputIntersection
(/ lineSeg1 lineSeg2 line1 line2 ip)
(setq lineSeg1 (editor:EntselLine "線分1を選択")
lineSeg2 (editor:EntselLine "線分2を選択")
)
;; 線分1を含む直線の方程式を取得
(setq line1
(line:GetEquation
(line:GetStartPoint lineSeg1)
(line:GetEndPoint lineSeg1)
)
)
;; 線分2を含む直線の方程式を取得
(setq line2
(line:GetEquation
(line:GetStartPoint lineSeg2)
(line:GetEndPoint lineSeg2)
)
)
;; 交点を出力
(if (setq ip (line:GetIntersection line1 line2))
(progn
(princ "\n交点の座標 : ") (princ ip)
)
(princ "\n2つの線分は平行です。\n")
)
(princ)
)
Subfunctions
;;;; == Subfunctions ==
;; 図形のDXF定義データの値を取得
(defun entity:GetDxf (g e)
(cond
((= (type e) 'ENAME) (cdr (assoc g (entget e))))
((listp e) (cdr (assoc g e)))
)
)
;; 図形のタイプを取得
(defun entity:GetType (e) (entity:GetDxf 0 e))
;; 線分図形をentsel 選択
(defun editor:EntselLine (msg / lineSeg)
;; 線分を選択
(while (null lineSeg)
(setvar 'ERRNO 0)
(setq lineSeg (car (entsel (strcat "\n" msg " :\n"))))
(cond
;; 空振り
((= 7 (getvar 'ERRNO))
(princ "\n... 空振り! 再選択 ...\n")
(setq lineSeg nil)
)
;; 空Enter
((= 52 (getvar 'ERRNO))
(princ "\n... 空Enter! 再選択 ...\n")
(setq lineSeg nil)
)
;; 図形が選択された
(lineSeg
(if (/= "LINE" (entity:GetType lineSeg))
(progn
(princ "\n... 線分ではありません! 再選択 ...\n")
(setq lineSeg nil)
)
(princ "\n... 線分が選択されました。\n")
)
)
)
)
lineSeg
)
;; 線分の始点を取得 // ss:line:sp
(defun line:GetStartPoint (e) (entity:GetDxf 10 e))
;; 線分の終点を取得 // ss:line:ep
(defun line:GetEndPoint (e) (entity:GetDxf 11 e))
;; 2点から直線の方程式を求める ax + by + c = 0
(defun line:GetEquation (p q / x1 y1 x2 y2 l)
(setq x1 (car p) y1 (cadr p)
x2 (car q) y2 (cadr q)
l (distance p q)
)
(if (> l 1.0e-08)
(mapcar
(function
(lambda (x) (/ x l))
)
(list (- y2 y1) (- x1 x2) (- (* x2 y1) (* x1 y2)))
)
)
)
;; 2直線の交点を求める
;; 2直線が平行の場合は nil を返す
(defun line:GetIntersection (l1 l2 / a1 b1 c1 a2 b2 c2 d)
(if (zerop
(setq a1 (car l1)
b1 (cadr l1)
c1 (caddr l1)
a2 (car l2)
b2 (cadr l2)
c2 (caddr l2)
d (- (* a1 b2) (* a2 b1))
)
)
nil
(list
(/ (- (* b1 c2) (* b2 c1)) d)
(/ (- (* a2 c1) (* a1 c2)) d)
)
)
)
2線分を選択、交点を出力するプログラム(inters関数使用)
AutoLISP関数の inters を使ったプログラム
;; inters 関数を使った場合
(defun c:c:SelectTwoLineAndOutputInters (/ lineSeg1 lineSeg2 ip)
(setq lineSeg1 (editor:EntselLine "線分1を選択")
lineSeg2 (editor:EntselLine "線分2を選択")
)
;; 交点を取得して出力
(if (setq ip (inters
(line:GetStartPoint lineSeg1)
(line:GetEndPoint lineSeg1)
(line:GetStartPoint lineSeg2)
(line:GetEndPoint lineSeg2)
nil
)
)
(progn
(princ "\n交点の座標 : ") (princ ip)
)
(princ "\n2つの線分は平行です。\n")
)
(princ)
)