0.はじめに

競技プログラミングでは制限時間内に解を求めるようなプログラムが求められます。競技プログラミングでなくとも、必要に応じてプログラムを高速化したい場面は無数にあります。逐次処理のプログラムを並行化することで処理を高速化する、並行プログラミング/マルチスレッドプログラミングを活用できる機会は多いのではないでしょうか。¹

本記事は Golang で逐次処理で計算できる処理を並行化/高速化することで、並行処理の威力や Golang の並行化の書きやすさを体感することを目標とします。

1.様々な計算の高速化

Go at Google: Language Design in the Service of Software Engineering にもあるように Golang の並行処理は CSP をベースにしており、並行処理が書きやすい言語と言えます。
Golang に組み込まれている goroutine や channel を用いて以下の計算処理を高速化することを試みます。

配列の総和
累積和
正方行列の積

1.1 配列の総和

高速化のための基本的なアイデア

まずは配列のそれぞれの要素の値を合計して表示させるようなシンプルな処理を高速化してみます。

基本的なアイデアは以下のようになります。

配列をいくつかの配列に分割する
分割したそれぞれの配列ごとに合計値を求める
2. で求めた結果を集約する

例として以下の $1$ から $10$ までの値がある配列の合計値を、上記のアイデアで計算してみます。答えは $55$ になります。

の処理を実施します。例では分割する数を $3$ としておきます。分割は以下のようになります。視覚的に分かりやすいように分割した配列それぞれに色をつけています。

の処理を実施します。結果は以下のようになります。

の処理を実施します。2. のそれぞれの分割した配列の合計を加算すると $6 + 15 + 34$ となり $55$ が得られます。

実装

この処理を Go で実装してみます。

sum/parallel_sum.go

// 並行化した実装
func ParallelSum(arr *[]int, concurrency int) int {
    n, m := len(*arr), concurrency
    c := make(chan int, m)

    // 配列を並行数で分割
    var start, end int
    for t := 0; t < m; t++ {
        start = n / m * (t)
        end = n / m * (t + 1)
        if t == m-1 {
            end = n
        }

        // 分割した配列の区間について、並行して総和を計算
        go func(arr *[]int, start, end int) {
            tmp := 0
            for i := start; i < end; i++ {
                tmp += (*arr)[i]
            }
            c <- tmp
        }(arr, start, end)
    }

    // 並行して計算した結果を集約
    sum := 0
    for i := 0; i < m; i++ {
        sum += <-c
    }
    return sum
}

// ナイーブな実装
func Sum(arr *[]int) int {
    ret := 0
    for i := 0; i < len(*arr); i++ {
        ret += (*arr)[i]
    }
    return ret
}

実験

本記事のすべての実験は AWS の Amazon EC2 c5.18xlarge² インスタンスの環境で確認しました。Go のバージョンは go1.12.7 linux/amd64 です。OS は Amazon Linux 2 です。

$ go version
go version go1.12.7 linux/amd64

$ cat /etc/system-release
Amazon Linux release 2 (Karoo)

上記の並行化した実装が実際にどれくらい高速化されるのか実験してみます。

ベンチマークのコードは以下です。

sum/sum_test.go

var (
    array       []int
    ans         int
)

func init() {
    rand.Seed(time.Now().UnixNano())
    for i := 0; i < pow(10, 9); i++ {
        tmp := rand.Intn(1 << 20)
        array = append(array, tmp)
        ans += tmp
    }
}

func BenchmarkParallelSum1(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 1)
}

func BenchmarkParallelSum2(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 2)
}

func BenchmarkParallelSum3(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 3)
}

func BenchmarkParallelSum4(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 4)
}

func BenchmarkParallelSum5(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 5)
}

func BenchmarkParallelSum6(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 6)
}

func BenchmarkParallelSum7(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 7)
}

func BenchmarkParallelSum8(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 8)
}

func BenchmarkParallelSum16(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 16)
}

func BenchmarkParallelSum24(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 24)
}

func BenchmarkParallelSum32(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 32)
}

func BenchmarkParallelSum36(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 36)
}

func BenchmarkParallelSum64(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 64)
}

func BenchmarkParallelSum128(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 128)
}

func BenchmarkParallelSum256(b *testing.B) {
    b.ResetTimer()
    ParallelSum(&array, 256)
}

func BenchmarkSum(b *testing.B) {
    b.ResetTimer()
    Sum(&array)
}

func pow(a, exp int) int {
    ret := 1
    for i := 0; i < exp; i++ {
        ret *= a
    }
    return ret
}

ベンチマークしたときのコマンドは以下です。明示的に³ 反復回数を $1000$ 万回としています。

$ go test --bench . -benchtime=10000000x

実験結果

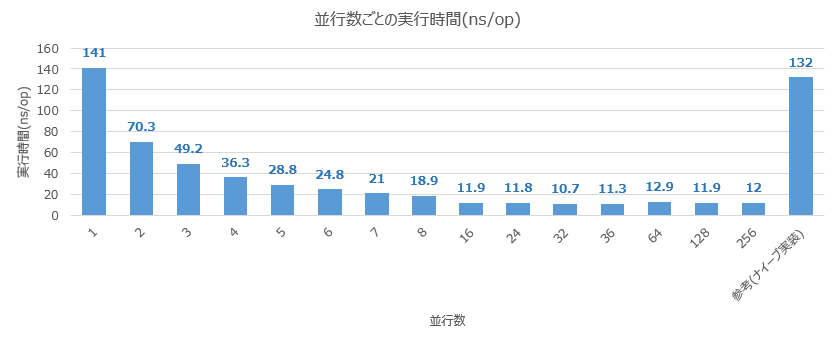
実験結果は以下のようになりました。

並行数が $1$ のときにが $141$ ns です。並行数を水平に $2,\ 3,\ 4,\ 5,\ \cdots$ と変化させると $70.3,\ 49.2,\ 36.3,\ 28.8,\ \cdots$ となっていることがわかります。
$\displaystyle \frac{141}{2} = 70.5,\ \frac{141}{3} = 47,\ \frac{141}{4} = 35.25,\ \frac{141}{5} = 28.2$ ですから、実験結果と比較すると、実験で得られた結果は非常にきれいにスケールしていることがわかります。

なお、最速は並行数は $32$ のときに $10.7$ ns となっています。その後は並行数を増やしても実行時間が改善されることはありませんでした。

1.2 累積和

累積和とは

累積和とは配列上の任意の区間の総和を高速に求める手法です。累積和がどのようなものか、またその応用についての説明はこちらが詳しいです。

端的に言うと、累積和は以下で定義されるものです。

配列 $a_0,\ a_1,\ a_2,\ \dots,\ a_{N-1}$ に対して、配列 $s_0,\ s_1,\ s_2,\ \dots,\ s_{N-1}$ を以下のように定めたもの

$s_0 = a_0$
$s_1 = a_0 + a_1$
$s_2 = a_0 + a_1 + a_2$
$\cdots$
$s_{N-1} = a_0 + a_1 + a_2 + \cdots + a_{N-1}$

なお、累積和 $s_0$ を $0$ とするか $a_0$ とするかは意見が分かれるところですが、本記事では $s_0 = a_0$ としておきます。

$1$ から $16$ までの配列の累積和は以下のようになります。

もとの配列がこちらです。

上記配列の累積和を求めると以下のようになります。

高速化のための基本的なアイデア

累積和計算高速化の基本的なアイデアは以下のようになります。

配列をいくつかの配列に分割する
分割したそれぞれの配列ごとに累積和を求める
2. で求めたそれぞれの累積和の一番最後の値の累積和を求める
3. で求めた結果を分割する前の配列に足し込む

となります。2.1 配列の合計のアイデアと似ていますが、計算の過程で前の計算結果を利用するところが異なる点のひとつです。

$1$ から $16$ までの配列の累積和計算の高速化を図解してみます。今回は $4$ 並列で計算することにします。
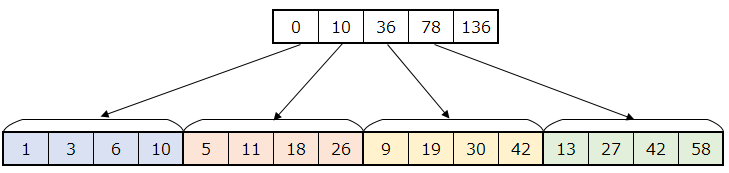
「2. 分割したそれぞれの配列ごとに累積和を求める」の処理をしたあとの配列は以下のようになります。$4$ 分割した配列それぞれで独立して累積和を計算しています。

「3. 2. で求めたそれぞれの累積和の一番最後の値の累積和を求める」は以下のようになります。
以下の図のようにそれぞれの分割した配列の最後の値を利用します。

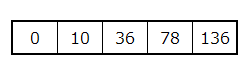
$0$ と上記の値のみで構成された以下の図の配列に対して累積和を計算します。

累積和計算後は以下です。

「4. 3. で求めた結果を分割する前の配列に足し込む」の計算は以下のようになります。

上記の計算によって、求めるべき以下の累積和が求めることができました。

この方法で常に正しい累積和が得られることは、累積和の定義から明らかです。

実装

さて、求める方法は分かったので Go で実装しましょう！

累積和の並行化では、計算過程で待ち合わせが必要です。いくつかの方法がありますが、今回は sync.WaitGroup によって待ち合わせを実装しています。

sum/cumulative_sum.go

// 並行化した実装
func ParallelCumulativeSum(arr *[]int, concurrency int) {
    n, m := len(*arr), concurrency
    tmpArray := make([]int, m+1)

    // 配列を並行数で分割
    wg := &sync.WaitGroup{}
    var start, end int
    for t := 0; t < m; t++ {
        start = n / m * (t)
        end = n / m * (t + 1)
        if t == m-1 {
            end = n
        }

        // 分割した配列ごとに累積和を計算
        wg.Add(1)
        go func(arr *[]int, start, end, t int) {
            defer wg.Done()
            for i := start; i < end-1; i++ {
                (*arr)[i+1] += (*arr)[i]
            }
            tmpArray[t+1] = (*arr)[end-1]
        }(arr, start, end, t)
    }

    // 分割した配列の累積和の並行処理の計算が全て完了するまで待機
    wg.Wait()

    // 分割した配列の累積和の一番最後の値の累積和を計算
    for i := 0; i < m; i++ {
        tmpArray[i+1] += tmpArray[i]
    }

    // 累積和の値を並行して配列に加算
    for t := 0; t < m; t++ {
        start = n / m * (t)
        end = n / m * (t + 1)
        if t == m-1 {
            end = n
        }

        wg.Add(1)
        go func(arr *[]int, start, end int, t int) {
            defer wg.Done()
            for i := start; i < end; i++ {
                (*arr)[i] += tmpArray[t]
            }
        }(arr, start, end, t)
    }
    wg.Wait()
}

// ナイーブな実装
func CumulativeSum(arr *[]int) {
    for i := 0; i < len(*arr)-1; i++ {
        (*arr)[i+1] += (*arr)[i]
    }
}

実験

ベンチマークのコードは以下です。

sum/sum_test.go

func BenchmarkParallelCumulativeSum1(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 1)
}

func BenchmarkParallelCumulativeSum2(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 2)
}

func BenchmarkParallelCumulativeSum3(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 3)
}

func BenchmarkParallelCumulativeSum4(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 4)
}

func BenchmarkParallelCumulativeSum5(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 5)
}

func BenchmarkParallelCumulativeSum6(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 6)
}

func BenchmarkParallelCumulativeSum7(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 7)
}

func BenchmarkParallelCumulativeSum8(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 8)
}

func BenchmarkParallelCumulativeSum16(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 16)
}

func BenchmarkParallelCumulativeSum24(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 24)
}

func BenchmarkParallelCumulativeSum32(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 32)
}

func BenchmarkParallelCumulativeSum36(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 36)
}

func BenchmarkParallelCumulativeSum64(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 64)
}

func BenchmarkParallelCumulativeSum128(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 128)
}

func BenchmarkParallelCumulativeSum256(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    ParallelCumulativeSum(&cArray, 256)
}

func BenchmarkCumulativeSum(b *testing.B) {
    cArray := make([]int, len(array))
    copy(cArray, array)
    b.ResetTimer()
    CumulativeSum(&cArray)
}

ベンチマークしたときのコマンドは以下です。明示的に反復回数を $1000$ 万回としています。

$ go test --bench . -benchtime=10000000x

実験結果

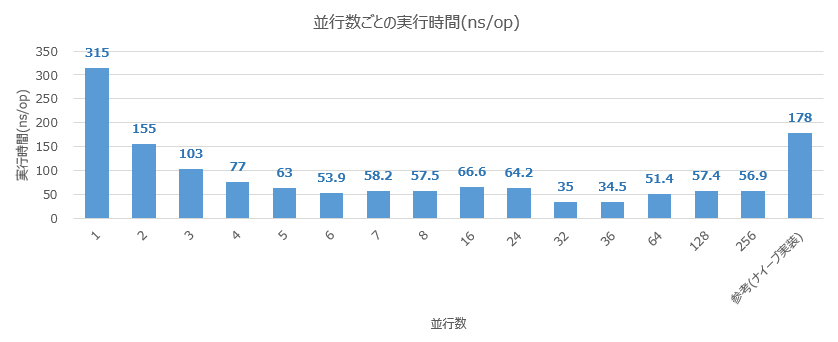
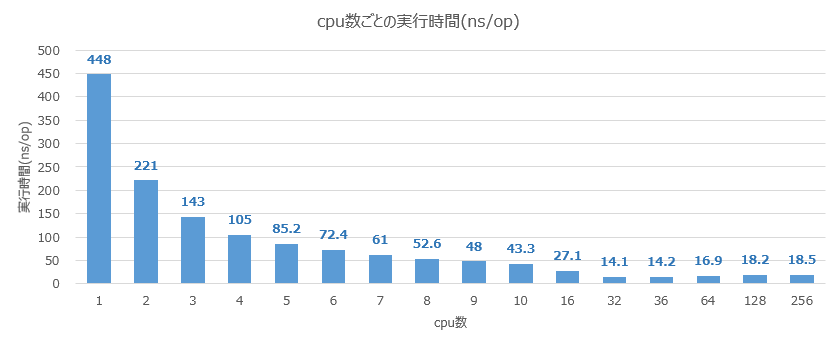
実験結果は以下のようになりました。

並行数が $1$ のときは、ナイーブな実装よりも $2$ 倍程度実行時間が伸びています。スケールに関しては並行数が $6$ までのときはきれいにスケールしていることがわかります。最良値は並行数が $36$ のときで $34.5$ ns でした。並行数を $36$ よりも大きくすると最良値よりも実行時間が悪化していることがわかります。

1.3 正方行列の積 ⁴

高速化のための基本的なアイデア

行列の積は一般的に以下で定義されます。

行列 $A=(a_{ij}),B=(b_{ij})$ に対して $C=AB=(c_{ij})$ であって、$c_{ij}=\sum_{k=1}^na_{ik}b_{kj}$

各行列の成分は独立に計算できることから、 それぞれの成分計算を並行化 することができます。

ただし、 $C$ の各成分計算 $(c_{ij})$ をすべて並行化すると goroutine の数は元の行列のサイズを $N$ とするとき $N^2$ になります。$N=1000$ 程度を想定しているので、$N^2={1000}^2=1000000$ は制御する goroutine 数が過剰にも思えます⁵。また、どちらも $2$ 重ループの計算が必要であることから、制御する goroutine の数は $N$ で抑えるのが良さそうです。

今回は実験として goroutine 数を $N$ と $N^2$ の $2$ つのパターンに分けて実験してみます。

実装

matrix/matrix.go

type Matrix [][]int

// N^2 個の成分計算をすべて並行化
func ParallelAllProductMatrix(a, b *Matrix) *Matrix {
    n := len(*a)
    c := make(Matrix, n)

    wg := &sync.WaitGroup{}
    for i := 0; i < n; i++ {
        c[i] = make([]int, n)
        for j := 0; j < n; j++ {
            wg.Add(1)

            // 成分ごとに並行化して計算
            go func(i, j int) {
                defer wg.Done()
                value := 0
                for k := 0; k < n; k++ {
                    value += (*a)[i][k] * (*b)[k][j]
                }
                c[i][j] = value
            }(i, j)
        }
    }
    wg.Wait()

    return &c
}

// N^2 個の成分計算を N つの goroutine で並行化
func ParallelRowProductMatrix(a, b *Matrix) *Matrix {
    n := len(*a)
    c := make(Matrix, n)

    wg := &sync.WaitGroup{}
    for i := 0; i < n; i++ {
        wg.Add(1)
        c[i] = make([]int, n)

        // 行ごとに並行化して計算
        go func(i int) {
            defer wg.Done()
            for j := 0; j < n; j++ {
                value := 0
                for k := 0; k < n; k++ {
                    value += (*a)[i][k] * (*b)[k][j]
                }
                c[i][j] = value
            }
        }(i)
    }
    wg.Wait()

    return &c
}

// ナイーブな実装
func ProductMatrix(a, b *Matrix) *Matrix {
    n := len(*a)
    c := make(Matrix, n)

    for i := 0; i < n; i++ {
        c[i] = make([]int, n)
        for k := 0; k < n; k++ {
            for j := 0; j < n; j++ {
                c[i][j] += (*a)[i][k] * (*b)[k][j]
            }
        }
    }

    return &c
}

実験

ベンチマークのコードは以下です。

matrix/matrix_test.go

var (
    a, b Matrix
)

func init() {
    rand.Seed(time.Now().UnixNano())
    n := 1000

    // make random matrix
    a, b = make(Matrix, n), make(Matrix, n)
    for i := 0; i < n; i++ {
        a[i] = make([]int, n)
        b[i] = make([]int, n)
        for j := 0; j < n; j++ {
            a[i][j] = rand.Intn(1 << 20)
            b[i][j] = rand.Intn(1 << 20)
        }
    }
}

func BenchmarkParallelAllProductMatrix(bench *testing.B) {
    bench.ResetTimer()
    ParallelAllProductMatrix(&a, &b)
}

func BenchmarkParallelRowProductMatrix(bench *testing.B) {
    bench.ResetTimer()
    ParallelRowProductMatrix(&a, &b)
}

func BenchmarkProductMatrix(bench *testing.B) {
    bench.ResetTimer()
    ProductMatrix(&a, &b)
}

この実験では制御する goroutine 数は $N$ と $N^2$ と固定して実装しています。並行数を制御するために、ベンチマーク実行の際に -cpu で cpu 数( GOMAXPROCS )を制御して実験しました。以下のテスト用シェルを作成し、実行しました。

test.sh

#!/bin/bash

for cnt in 1 2 3 4 5 6 7 8 9 10 16 32 36 64 128 256
do
  echo "[DEBUG] start matrix_test.go -cpu $cnt"
  /usr/local/go/bin/go test --bench . -benchtime=10000000x -cpu=$cnt
  echo ""
done

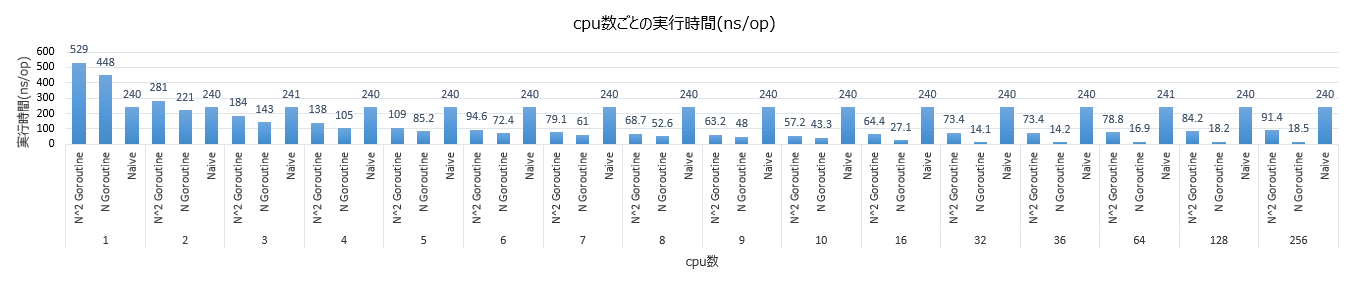
実験結果

実験結果は以下のようになりました。$N$ の goroutine 数の並行化の結果が $N^2$ の goroutine 数の並行化の結果よりも良い結果が得られています。
最良の実行時間は cpu 数が $32$ のときに $14.1$ ns となっています。

cpu 数が $N$ のときの結果をみると cpu 数が $32$ あたりまではきれいにスケールしていることがわかります。

2. まとめ

Golang で自然に逐次処理を並行化することができました。並行数による高速化の限界は見定める必要がありますが、並行化によって高速化することができました。

ただし 2019/7/23 現在、AtCoder の実行環境のスレッド数は、コードテストからスレッド数を調査したところ $2$ でした。そのため、一般的に想定解よりもオーダーが悪い実装を並行処理で高速化して、正答することは難しそうです。 ↩
vCPU: $72$, 物理CPU: $36$, メモリ: $144$ GiB https://aws.amazon.com/jp/ec2/instance-types/c5/ ↩
Go1.12 から利用できるようになりました。 https://tip.golang.org/doc/go1.12 ↩
今回は自前で行列計算を実装しましたが、行列を扱うパッケージとしては gonum などがあります。 ↩
ただし $N=1000$ としても cpu 数に対して制御する goroutine の数は過剰でしょう。 ↩

Golangを用いた様々な計算の高速化

0.はじめに

1.様々な計算の高速化

1.1 配列の総和

高速化のための基本的なアイデア

実装

実験

実験結果

1.2 累積和

累積和とは

高速化のための基本的なアイデア

実装

実験

実験結果

1.3 正方行列の積 4

高速化のための基本的なアイデア

実装

実験

実験結果

2. まとめ

1.3 正方行列の積 ⁴