LoginSignup
8
6

More than 3 years have passed since last update.

@tttamaki(Toru Tamaki)

Pyroでいろいろな分布を最尤推定

Posted at

Pyroでいろいろな1次元の連続確率分布のパラメータを最尤推定する．

  • 正規分布
  • ベータ分布
  • T分布
  • ラプラス分布
  • コーシー分布
  • 指数分布
  • ガンマ分布
  • ガンベル分布

最尤推定は解析解が得られるものもあるが（正規分布など），
反復法によるものもある（ガンマ分布など）．
また分布によって方法が異なり，実装がバラバラ．
それをここではpyroを使って，
確率分布をmodelで定義するだけで
あとは同一のコードで反復法で最尤推定を行う．

詳しく解説するのは正規分布だけ．他のコードは以下のgistにあり．
https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e

Tips

  • ガイドにはAutoDeltaを使う（点推定）
  • 学習時のモニタはhook
  • 推定値はpoutine.traceで持ってくる

準備

準備．notebook用です
import matplotlib.pyplot as plt
%matplotlib inline

from collections import defaultdict
import os

import numpy as np


import torch
import torch.distributions.constraints as constraints

import pyro
from pyro.optim import Adam
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import AutoDelta, AutoNormal
from pyro.infer.autoguide.initialization import init_to_feasible

# import pyro.poutine as poutine
from pyro import poutine

pyro.enable_validation(True)
pyro.set_rng_seed(101)


from tqdm.notebook import tqdm
import daft

1次元正規分布

真のパラメータ

真のmとstdをランダムに作成
true_m = np.random.rand() * 10
true_std = np.abs(np.random.rand() * 2)
print('m =', true_m, 'std =', true_std)

x_range = np.arange(true_m - 4*true_std, true_m + 4*true_std, 0.01)
x_max = x_range.max()
x_min = x_range.min()
print('x_range: from {0:.3f} to {1:.3f}'.format(x_min, x_max))

m = 2.3235366181476067 std = 0.16712286732668735
x_range: from 1.655 to 2.985

データ作成

真の分布からデータをサンプリング
# sampling
target_dist = dist.Normal(true_m, true_std)
data = torch.tensor([target_dist() for i in range(100)])
# pdf：分布関数
true_y = [target_dist.log_prob(torch.tensor([x])).exp() for x in x_range]


fig = plt.figure(figsize=(10,5))
plt.plot(x_range, true_y, c='k', label=r'Normal(m,$\sigma$)')
plt.hist(data, range=(x_min, x_max), bins=100, density=True, alpha=0.2, label=r'observed data $\{x_i\}$')

plt.title(r'm={0:.3f} $\sigma$={1:.3f}'.format(true_m, true_std))

plt.ylim(0,)
plt.xlabel('x')
plt.legend()
plt.savefig('obs-data')
plt.show()

normal_obs-data.png

ちなみに最尤推定の解析解は，正規分布の場合は平均と分散．

ml_m = data.numpy().mean()
ml_std = data.numpy().std()
print('m={0:.3f}, sigma={1:.3f}'.format(ml_m, ml_std))

m=2.318, sigma=0.157

グラフィカルモデル

モデルmodelは以下の構造を持つ．

  • $p_\theta(X)$
  • $X = {x_1, \ldots, x_N }$は観測されたデータ
  • パラメータは$\theta = { m, \sigma }$
    • $x_i \sim \mathrm{Gauss}(m, \sigma)$

normal-graph.png

グラフィカルモデルをdaftで描く
pgm = daft.PGM()

pgm.add_node("xn", r"$x_n$", 2, 1, observed=True)
pgm.add_node("m", "m", 1.5, 2, fixed=True)
pgm.add_node("std", r"$\sigma$", 2.5, 2, fixed=True)
pgm.add_edge("m", "xn")
pgm.add_edge("std", "xn")
pgm.add_plate([1, 0.5, 2, 1], label=r"$n = 1, \ldots, N$", shift=-0.2)

pgm.show()  # render and show

モデルとガイド

モデルは，pyro.paramでパラメータにmとstdを設定．

モデル
def model(data=None):

    # 推定初期値は0.0にする
    m = pyro.param("m", torch.tensor(0.0))

    # 推定初期値は1.0にする
    # std > 0なので，positive制約を追加
    std = pyro.param("std", torch.tensor(1.0), constraint=constraints.positive)

    # dataはすべてのデータを表す（つまりベクトル・リスト・アレイ）
    with pyro.plate('observe_data'):  # 各観測obsは独立を仮定するからplateを利用
        pyro.sample('obs', dist.Normal(m, std), obs=data)  # vector-plateを利用

ガイドには点推定のAutoDeltaを使用

guide = AutoDelta(
    poutine.block(model, hide=['obs']),  # modelのobsを隠し，それ以外（mとstd）を使う
    init_loc_fn=init_to_feasible  # 初期値は妥当な値
)

推定準備

adam_params = {"lr": 0.005, "betas": (0.95, 0.999)}
optimizer = Adam(adam_params)  # とりあえずAdam


svi = SVI(model=model,
          guide=guide,
          optim=optimizer,
          loss=Trace_ELBO()
         )

パラメータの初期化とhookの設定．パラメータの途中の値を保存するため．

pyro.clear_param_store()  # pyro.get_param_store()は空になる

svi.loss(model, guide, data)  # これを一回やらないとpyro.get_param_store()は空のママ

trace_dic = defaultdict(list)  # 値を保存する（このリストをここではtraceと呼ぶことにする）
for name, value in pyro.get_param_store().named_parameters():
    print('tracing', name, type(value), value)
    # hookは勾配計算毎に呼び出される．勾配の値gradは無視，nameを利用してparam(name)で値を取得してdicのlistに追加
    value.register_hook(lambda grad, name=name: trace_dic[name].append(pyro.param(name).item()))

tracing m <class 'torch.Tensor'> tensor(0., requires_grad=True)
tracing std <class 'torch.Tensor'> tensor(0., requires_grad=True)

推定

反復推定．

num_steps = 5000

with tqdm(range(num_steps)) as pbar:
    for i,p in enumerate(pbar):

        loss = svi.step(data)  # 勾配計算，更新

        trace_dic['loss'].append(loss)

        if i > 100 and np.isclose(trace_dic['loss'][-100], loss):
            break  # 100回前と値が変わらなければ収束

        if i % 10 == 0:  # 毎回表示すると早すぎて見えないので10回に1回表示
            pbar.set_postfix(loss=loss)

収束の様子

fig = plt.figure(figsize=(10,5))
plt.plot(trace_dic['loss'])
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
savefig("loss")
plt.show()


fig = plt.figure(figsize=(15,5))

for i,param in enumerate(['m', 'std']):
    plt.subplot(1,2,i+1)
    plt.plot(trace_dic[param])
    plt.ylabel(param)

plt.tight_layout()
savefig("params")
plt.show()

lossの減少の様子
normal_loss.png

パラメータmとstdの収束の様子
normal_params.png

結果

最尤推定値と真値の比較

trace = poutine.trace(model).get_trace()

print('m', trace.nodes['m']['value'].item(), 'true m', true_m)
print('std', trace.nodes['std']['value'].item(), 'true std', true_std)

ほぼ真値に近い．

m 5.083353042602539 true m 5.163986277024462
std 1.1655045747756958 true std 1.1413351737362796

最尤推定値の分布と真の分布の比較

fig = plt.figure(figsize=(10,5))


# traceでパラメータを取得
trace = poutine.trace(model).get_trace()
m = trace.nodes['m']['value'].item()
std = trace.nodes['std']['value'].item()

# generate a pdf
estimated_dist = dist.Normal(m, std)
y = [estimated_dist.log_prob(torch.tensor([x])).exp() for x in x_range]


# plot
plt.plot(x_range, y, c='k', label='ML estimated pdf')
plt.plot(x_range, true_y, c='r', label=r'true pdf')
plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, l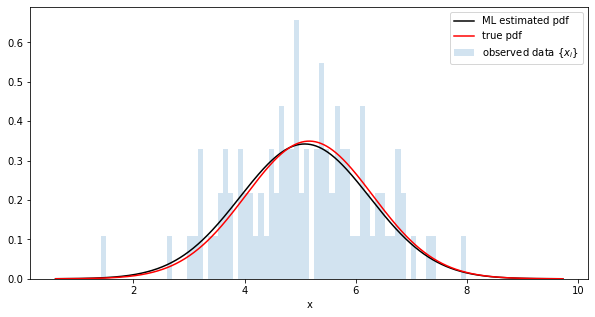![normal_sampled-pdf.png](https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/44835/0d36d454-fce6-9b62-a42c-a8aa546733f6.png)
abel=r'observed data $\{x_i\}$')


plt.xlabel('x')
plt.legend()
savefig("sampled-pdf")
plt.show()

normal_sampled-pdf.png

推定した分布からサンプリングして元データと比較

fig = plt.figure(figsize=(10,5))

obs = []
for _ in range(5000):
    trace = poutine.trace(model).get_trace()
    obs.append(trace.nodes['obs']['value'].item())

plt.xlabel('posterior samples')

plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, label=r'observed data $\{x_i\}$')
plt.hist(obs, range=(x_min, x_max), bins=100, alpha=0.2, density=True, color='r', label=r'sampled data$')

plt.legend()
savefig("pdf-obs")
plt.show()

normal_pdf-obs.png

その他の分布

以下は元データ（青），真の分布（赤），最尤推定パラメータでの推定分布（黒）のみを表示．

コードは
https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e
にあります．

ベータ分布

beta_sampled-pdf.png

t分布

student-t_sampled-pdf.png

ラプラス分布

laplace_sampled-pdf.png

コーシー分布

cauchy_sampled-pdf.png

指数分布

Exponential_sampled-pdf.png

ガンマ分布

gamma_sampled-pdf.png

ガンベル分布

gumbel_sampled-pdf.png

8
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
6