 この記事の目的
この記事の目的
量子ゲート計算における回転について、数式やブロッホ球を用いてしっかり学びます。
また。次の章では実際に回転ゲートを用いたプログラミングを行います。
 回転とは
回転とは
量子計算における回転とは、ブロッホ球のある量子状態に対して操作を行い、別の量子状態へ変化(発展)させる操作のことを言います。特に、前章で確認したブロッホ球上のある状態(位置)と軸との間の角$\theta$、$\phi$(※1)に対して、この角度を変えることで様々な量子状態を実現させることができます。
※1 … 以下参照
![]() 量子コンピュータの基本 - ブロッホ球の数式をしっかり解説
量子コンピュータの基本 - ブロッホ球の数式をしっかり解説
https://qiita.com/ttabata/items/0e839d03963d656551e0
ブロッホ球上で角$\theta$、$\phi$を変えるためには、X、Y、Z軸を軸の中心として回転させるので、この操作のことを回転(または回転操作)と呼びます。
 回転行列(回転ゲート)を学ぶ
回転行列(回転ゲート)を学ぶ
回転操作において、実際に量子状態を回転させるには回転行列(回転ゲート)を使用します。
補足として、回転行列はユニタリ行列で、ある量子状態にユニタリ行列を適用して別の量子状態に変化させることを一般にユニタリ発展と呼びます。
1. X、Y、Z軸上の回転行列
X、Y、Z軸それぞれの軸を中心とした回転操作で使用する回転行列は以下に定義されます。
**注意:**以下で表記される角$\Delta\theta$はブロッホ球上の各軸とのなす角を表すのではなく、回転させる角度(の増減)を意味します。また、$i$は虚数単位です。
X軸回転 \mkern{2em} R_x(\Delta\theta) = \begin{pmatrix}
\cos(\frac{\Delta\theta}{2}) & -i\sin(\frac{\Delta\theta}{2}) \\
-i\sin(\frac{\Delta\theta}{2}) & \cos(\frac{\Delta\theta}{2}) \end{pmatrix} \mkern{2em} ... 式(1)\\
Y軸回転 \mkern{2em} R_y(\Delta\theta) = \begin{pmatrix}
\cos(\frac{\Delta\theta}{2}) & -\sin(\frac{\Delta\theta}{2}) \\
\sin(\frac{\Delta\theta}{2}) & \cos(\frac{\Delta\theta}{2}) \end{pmatrix} \mkern{2em} ... 式(2)\\
Z軸回転 \mkern{2em} R_z(\Delta\theta) = \begin{pmatrix}
\exp(-i\frac{\Delta\theta}{2}) & 0 \\
0 & \exp(i\frac{\Delta\theta}{2}) \end{pmatrix} \mkern{2em} ... 式(3)
2. 任意回転の回転行列
X、Y、Z軸上で個別に回転させるものではなく、それら全方向を一度に回転させて計算を行うための行列です。この回転行列の一つは、Y、Z軸の二つの軸の回転成分を用いて表現されます。これをZ-Y分解と呼びます。
以下のユニタリ行列で表します。
\begin{align}
U_{Z-Y} &= e^{i\gamma}R_z(\Delta\phi)R_y(\Delta\theta)R_z(\Delta\lambda)\\
&= \begin{pmatrix}
e^{i(\gamma-\frac{\Delta\phi}{2}-\frac{\Delta\lambda}{2})}\cos(\frac{\Delta\theta}{2}) & -e^{i(\gamma-\frac{\Delta\phi}{2}+\frac{\Delta\lambda}{2})}\sin(\frac{\Delta\theta}{2}) \\
e^{i(\gamma+\frac{\Delta\phi}{2}-\frac{\Delta\lambda}{2})}\sin(\frac{\Delta\theta}{2}) & e^{i(\gamma+\frac{\Delta\phi}{2}+\frac{\Delta\lambda}{2})}\cos(\frac{\Delta\theta}{2}) \end{pmatrix} \mkern{2em} ... 式(4)
\end{align}
また、以下のようにX、Y軸の二つの軸の回転成分で表現することもできます。これをX-Y分解と呼びます。
\begin{align}
U_{X-Y} &= e^{i\gamma}R_x(\Delta\phi)R_y(\Delta\theta)R_x(\Delta\lambda)\\
&= e^{i\gamma}\begin{pmatrix}
u_{11} & u_{12} \\
u_{21} & u_{22} \end{pmatrix} \mkern{2em} ... 式(5)
\end{align}
ここで$u_{11},u_{12},u_{21},u_{22}$は以下となります。
u_{11} = \cos(\frac{\Delta\theta}{2})\Big(\cos(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})-\sin(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})\Big)\\
\mkern{4em} -i\sin(\frac{\Delta\theta}{2})\Big(\sin(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})-\cos(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})\Big) \\
u_{12} = -\sin(\frac{\Delta\theta}{2})\Big(\sin(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})+\cos(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})\Big)\\
\mkern{4em} -i\cos(\frac{\Delta\theta}{2})\Big(\cos(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})+\sin(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})\Big) \\
u_{21} = \sin(\frac{\Delta\theta}{2})\Big(\cos(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})+\sin(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})\Big)\\
\mkern{4em} -i\cos(\frac{\Delta\theta}{2})\Big(\sin(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})+\cos(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})\Big) \\
u_{22} = -\cos(\frac{\Delta\theta}{2})\Big(\sin(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})-\cos(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})\Big)\\
\mkern{4em} +i\sin(\frac{\Delta\theta}{2})\Big(-\cos(\frac{\Delta\phi}{2})\sin(\frac{\Delta\lambda}{2})+\sin(\frac{\Delta\phi}{2})\cos(\frac{\Delta\lambda}{2})\Big)
![]() 実際の任意回転行列
実際の任意回転行列
式(4)の回転行列は、さらに式を変形して以下のように整理します。
U_{Z-Y} = e^{i(\gamma-\frac{\Delta\theta}{2}-\frac{\Delta\lambda}{2})}
\begin{align}
\begin{pmatrix}
\cos(\frac{\Delta\theta}{2}) & -e^{i\Delta\lambda}\sin(\frac{\Delta\theta}{2}) \\
e^{i\Delta\phi}\sin(\frac{\Delta\theta}{2}) & e^{i(\Delta\lambda+\Delta\phi)}\cos(\frac{\Delta\theta}{2}) \end{pmatrix} \mkern{2em} ... 式(6)
\end{align}
上記で用いられる以下の項は大域位相(全体位相)と呼ばれます。
e^{i(\gamma-\frac{\Delta\theta}{2}-\frac{\Delta\lambda}{2})}
これはブロッホ球上の回転操作や回転角に直接関わることはなく、また実際に観測される量ではないため、回転行列では省略されます。
よって、実際の任意回転行列は以下を使用します。
**注意:**以下では角度の増減を表す記号$\Delta$を省略し、一般的な数式として表記しましたが、角$\theta$、$\phi$はそれぞれあくまで増減量を取ります。
\begin{pmatrix}
\cos(\frac{\theta}{2}) & -e^{i\lambda}\sin(\frac{\theta}{2}) \\
e^{i\phi}\sin(\frac{\theta}{2}) & e^{i(\lambda+\phi)}\cos(\frac{\theta}{2}) \end{pmatrix}
\mkern{2em} ... 式(7)
 代表的な回転操作(X,Y,Z軸回転)と回転計算結果
代表的な回転操作(X,Y,Z軸回転)と回転計算結果
ここでは実際にX、Y、Z軸それぞれの軸ごとに90度($\pi/2$:ラジアン)、180度($\pi$)の回転操作を行い、量子状態がブロッホ球上でどのように動くか、また回転計算後の状態を確認します。
※計算では回転の角度を**弧度法(単位:ラジアン)**を用いて表記しています。
※ブロッホ球上の回転前の位置を赤矢印、回転後の位置を青矢印で表現しています。
1. X軸上で90度(π/2)回転
X軸上の回転を行うため、式(1)を使用して回転操作(回転計算)を行います。今、初期状態をブロッホ球上の北極点とすると、回転前の量子状態(赤矢印)は$|0〉$となります。また、回転後の量子状態(青矢印)を$|\psi〉$とします。

回転操作はX軸方向に90度(π/2)回転(※2)させれば良いことがわかります。
回転の計算は以下のようになります。
\begin{align}
|\psi〉&= R_x(\frac{\pi}{2})|0〉\\
&= \begin{pmatrix}
\cos(\frac{\frac{\pi}{2}}{2}) & -i\sin(\frac{\frac{\pi}{2}}{2}) \\
-i\sin(\frac{\frac{\pi}{2}}{2}) & \cos(\frac{\frac{\pi}{2}}{2}) \end{pmatrix}
\begin{pmatrix} 1 \\ 0 \end{pmatrix} \\
&= \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 0 \end{pmatrix}
-i\frac{1}{\sqrt{2}}\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\
&= \frac{1}{\sqrt{2}}|0〉-i\frac{1}{\sqrt{2}}|1〉\mkern{2em}... 式(8)
\end{align}
※2 … 回転方向は軸の正の方向に右回りと定義します。
回転操作後の量子状態は式(8)となりますが、ここで、さらにこれをブロッホ球上の位置及び軸となす角がわかる式に直すと、以下のように変形することができます。
\begin{align}
\frac{1}{\sqrt{2}}|0〉-i\frac{1}{\sqrt{2}}|1〉 &= \frac{1}{\sqrt{2}}|0〉+e^{-i\frac{\pi}{2}}\frac{1}{\sqrt{2}}|1〉
\end{align}\\
∵オイラーの公式より\cos(-\frac{\pi}{2})+i\sin(-\frac{\pi}{2}) = e^{-i\frac{\pi}{2}}\\
右辺=\cos(\frac{\pi}{4})|0〉+e^{-i\frac{\pi}{2}}\sin(\frac{\pi}{4})|1〉\mkern{2em}... 式(9)\\
これより、\thetaについては、\frac{\theta}{2}=\frac{\pi}{4}、すなわち\theta=90度(\frac{\pi}{2})、\\
\phiについては、\phi=-\frac{\pi}{2}、すなわち\phi=-90度
上記の結果、$\theta$と$\phi$を見ると、ブロッホ球の青矢印に一致することがわかります。
2. X軸上で180度(π)回転
初期状態をブロッホ球上の北極点|0〉とし、式(1)のX軸回転行列を使用して回転操作(回転計算)を行います。
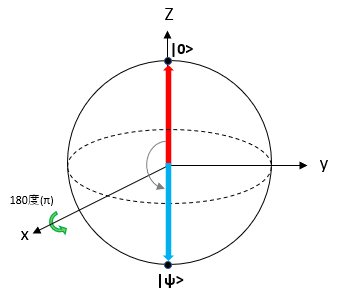
回転の計算は以下のようになります。
\begin{align}
|\psi〉&= R_x(\pi)|0〉\\
&= \begin{pmatrix}
\cos(\frac{\pi}{2}) & -i\sin(\frac{\pi}{2}) \\
-i\sin(\frac{\pi}{2}) & \cos(\frac{\pi}{2})
\end{pmatrix}
\begin{pmatrix} 1 \\ 0 \end{pmatrix}\\
&= \begin{pmatrix}
0 & -i \\ -i & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}\\
&= -i\begin{pmatrix} 0 \\ 1 \end{pmatrix}\\
&= -i|1〉\mkern{2em}... 式(10)
\end{align}
回転操作後の量子状態は式(10)となりますが、同様にブロッホ球上の位置及び軸となす角がわかる式に直すと、以下のようになります。
\begin{align}
式(10) &= 0・|0〉-i|1〉\\
&= \cos(\frac{\pi}{2})|0〉+e^{-i\frac{\pi}{2}}\sin(\frac{\pi}{2})|1〉
\mkern{2em}... 式(11)
\end{align}\\
これより、\thetaについては、\theta=180度(\pi)、\\
\phiについては、\phi=-\frac{\pi}{2}、すなわち\phi=-90度
上記の結果、$\theta$と$\phi$はブロッホ球の青矢印に一致することがわかります。
3. Y軸上で90度(π/2)回転
初期状態をブロッホ球上の北極点|0〉とし、式(2)のY軸回転行列を使用して回転操作(回転計算)を行います。

回転の計算は以下のようになります。
式(2)において$\theta$にπ/2を代入して、
\begin{align}
|\psi〉&= R_y(\frac{\pi}{2})|0〉\\
&= \begin{pmatrix}
\cos(\frac{\frac{\pi}{2}}{2}) & -\sin(\frac{\frac{\pi}{2}}{2}) \\
\sin(\frac{\frac{\pi}{2}}{2}) & \cos(\frac{\frac{\pi}{2}}{2})
\end{pmatrix}
\begin{pmatrix} 1 \\ 0 \end{pmatrix}\\
&= \begin{pmatrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}\\
&= \frac{1}{\sqrt{2}}\begin{pmatrix}1 & -1 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}\\
&= \frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ 1 \end{pmatrix}\\
&= \frac{1}{\sqrt{2}}\left\{\begin{pmatrix} 1 \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ 1 \end{pmatrix}\right\}\\
&= \frac{1}{\sqrt{2}}|0〉+\frac{1}{\sqrt{2}}|1〉\mkern{2em}... 式(12)
\end{align}
回転結果は上記となりました。これはアダマール変換(Hゲート変換)による重ね合せ状態と同じ結果となります。
ブロッホ球上の位置を確認すると以下となります。
\theta=\frac{\pi}{2} (90度)\\
\phi=0 (0度)
$\theta$と$\phi$はブロッホ球の青矢印の位置となります。
同様にして、Y軸上の180度(π)回転も計算することができます。
4. Z軸上で90度(π/2)回転
初期状態を式(12)の位置として、Z軸回転行列を使用して回転操作(回転計算)を行います。

上記のブロッホ球上で初期状態$|\psi_0〉$を式(12)とするため、以下のように$|\psi_0〉$を設定します。
|\psi_0〉= \frac{1}{\sqrt{2}}|0〉+\frac{1}{\sqrt{2}}|1〉
また、回転行列$R_z$は式(3)を用いて以下のように設定します。
\begin{align}
R_z(\frac{\pi}{2}) &= \begin{pmatrix}
exp(-i\frac{\frac{\pi}{2}}{2}) & 0 \\
0 & exp(i\frac{\frac{\pi}{2}}{2})
\end{pmatrix}\\
&= \begin{pmatrix}
exp(-i\frac{\pi}{4}) & 0 \\
0 & exp(i\frac{\pi}{4})
\end{pmatrix}\\
&= \begin{pmatrix}
e^{-i\frac{\pi}{4}} & 0 \\
0 & e^{i\frac{\pi}{4}}
\end{pmatrix}\\
&= \begin{pmatrix}
\cos\frac{\pi}{4}-i\sin\frac{\pi}{4} & 0 \\
0 & \cos\frac{\pi}{4}+i\sin\frac{\pi}{4}
\end{pmatrix}\\
&= \begin{pmatrix}
\frac{1}{\sqrt{2}}(1-i) & 0\\
0 & \frac{1}{\sqrt{2}}(1+i)
\end{pmatrix}\\
\end{align}
上記の条件を用いて、回転の計算は以下のようになります。
\begin{align}
|\psi〉&= R_z(\frac{\pi}{2})|\psi_0〉\\
&= \begin{pmatrix}
\frac{1}{\sqrt{2}}(1-i) & 0\\
0 & \frac{1}{\sqrt{2}}(1+i)
\end{pmatrix}\frac{1}{\sqrt{2}}\left\{
\begin{pmatrix} 1\\0\end{pmatrix}+\begin{pmatrix} 0\\1\end{pmatrix}
\right\}\\
&= \frac{1}{2}\left\{\begin{pmatrix} 1-i\\0\end{pmatrix}+\begin{pmatrix} 0\\1+i\end{pmatrix}\right\}\\
&= \frac{1}{2}(1-i)|0〉+\frac{1}{2}(1+i)|1〉\mkern{2em}... 式(13)
\end{align}
回転操作後の量子状態は式(13)となります。
ここで、ブロッホ球上の位置及び軸となす角がわかるように式を変形してみましょう。
\begin{align}
式(13) &= \frac{1}{2}(1-i)\Bigg(|0〉+\frac{1+i}{1-i}|1〉\Bigg)\\
&= \frac{1}{2}(1-i)\Big(|0〉+i|1〉\Big)\\&= \frac{1}{\sqrt{2}}(1-i)\left\{\frac{1}{\sqrt{2}}|0〉+\frac{1}{\sqrt{2}}i|1〉\right\}\mkern{2em}... 式(14)
\end{align}
式(14)についてもう少し詳しく見てみます。式(14)は前半の定数項$\frac{1}{\sqrt{2}}(1-i)$と、後半{ }(括弧)内部の以下の項に分けることができます。
\frac{1}{\sqrt{2}}|0〉+\frac{1}{\sqrt{2}}i|1〉\mkern{2em}... 式(15)
前半部分は回転角度に影響を持つ項ではなく、大域位相項と見なすことができます。
そして、後半の式(15)に注目しこの式をさらに変形すると以下の通りとなり、ブロッホ球上の位置$\theta$及び$\phi$を算出することができます。
\begin{align}
式(15) &= \cos(\frac{\pi}{4})|0〉+e^{i\frac{\pi}{2}}\sin(\frac{\pi}{4})|1〉\\
&= \cos(\frac{\frac{\pi}{2}}{2})|0〉+e^{i\frac{\pi}{2}}\sin(\frac{\frac{\pi}{2}}{2})|1〉\end{align}\\
よって、\theta=\frac{\pi}{2}、\phi=\frac{\pi}{2}
上記の結果、$\theta$と$\phi$はブロッホ球の青矢印に一致することがわかります。
5. Z軸上で180度(π)回転

初期状態$\psi_0$を上記「4. Z軸上で90度(π/2)回転」で回転操作で得られた状態(式(13))とし、これをZ軸方向に180度(π)だけ回転操作を行います。
回転行列$R_z$は式(3)を用いて以下とします。
\begin{align}
R_z(\pi) &= \begin{pmatrix}exp(-i\frac{\pi}{2}) & 0 \\
0 & exp(i\frac{\pi}{2})\end{pmatrix}\\
\end{align}
以下、回転計算を行います。
\begin{align}
|\psi〉&= R_z(\pi)|\psi_0〉\\
&= \begin{pmatrix}e^{-i\frac{\pi}{2}} & 0 \\
0 & e^{i\frac{\pi}{2}}\end{pmatrix}\left\{\frac{1}{2}(1-i)|0〉+\frac{1}{2}(1+i)|1〉\right\}\\
&= \frac{1}{2}\begin{pmatrix} -i & 0 \\ 0 & i \end{pmatrix}\left\{\begin{pmatrix} 1-i \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ 1+i \end{pmatrix}\right\}\\
&= \frac{1}{2}\left\{\begin{pmatrix} -i(1-i) \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ i(1+i) \end{pmatrix}\right\}\\
&= \frac{1}{2}\left\{\begin{pmatrix}-1-i \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ -1+i \end{pmatrix}\right\}\\
&= -\frac{1+i}{2}|0〉-\frac{1-i}{2}|1〉\mkern{2em}... 式(16)
\end{align}
回転操作後の量子状態は式(16)となりますが、同様にブロッホ球上の位置及び軸となす角がわかる式に直すと、以下のようになります。
\begin{align}
式(16) &= -\frac{1}{2}\left\{(1+i)|0〉+(1-i)|1〉\right\}\\
&= -\frac{1}{2}(1+i)\Big(|0〉+\frac{1-i}{1+i}|1〉\Big)\\
&= -\frac{1+i}{2}\Big(|0〉+\frac{1-i}{(1+i)(1-i)}|1〉\Big)\\
&= -\frac{1+i}{2}(|0〉-i|1〉)\\
&= -\frac{1+i}{\sqrt{2}}\Big(\frac{1}{\sqrt{2}}|0〉-\frac{1}{\sqrt{2}}i|1〉\Big)\\
&= -\Big(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\Big)\Big(\frac{1}{\sqrt{2}}|0〉-\frac{1}{\sqrt{2}}i|1〉\Big)\\
&= -e^{i\frac{\pi}{4}}\Big(\cos\frac{\pi}{4}|0〉+e^{-i\frac{\pi}{2}}\sin\frac{\pi}{4}|1〉\Big)
\end{align}
ここで、$-e^{i\frac{\pi}{4}}$は大域位相項となるため省略すると、計算結果は以下となります。
\cos\frac{\frac{\pi}{2}}{2}|0〉+e^{-i\frac{\pi}{2}}\sin\frac{\frac{\pi}{2}}{2}|1〉\mkern{2em}... 式(17)\\
よって、\theta=90度(\frac{\pi}{2})、\phi=-90度(-\frac{\pi}{2})
上記の結果、$\theta$と$\phi$はブロッホ球の青矢印に一致することがわかります。
 任意回転操作と回転計算結果
任意回転操作と回転計算結果
式(7)を使用した任意回転の計算方法について確認します。
まず、回転操作として以下を考えます。初期状態を式(12)とし、$\theta$として-45度、$\phi$として45度を取る回転を行います。

回転に関する式(7)のユニタリ行列を以下とします。位相回転が伴うため$\lambda$は0またはπを取りますが、ここでは0とします。πとした場合も結果的には同じとなります。
U=\begin{pmatrix}
\cos(\frac{-\frac{\pi}{4}}{2}) & -e^{i・0 }\sin(\frac{-\frac{\pi}{4}}{2}) \\
e^{i\frac{\pi}{4}}\sin(\frac{-\frac{\pi}{4}}{2}) & e^{i(0+\frac{\pi}{4})}\cos(\frac{-\frac{\pi}{4}}{2})
\end{pmatrix}\mkern{2em}... 式(18)
上記ユニタリ行列と式(12)より、回転操作の計算結果は以下となります。
\begin{align}
|\psi〉 &= U|\psi_0〉\\
&= \begin{pmatrix}
\cos(\frac{-\frac{\pi}{4}}{2}) & -e^{i・0 }\sin(\frac{-\frac{\pi}{4}}{2}) \\
e^{i\frac{\pi}{4}}\sin(\frac{-\frac{\pi}{4}}{2}) & e^{i(0+\frac{\pi}{4})}\cos(\frac{-\frac{\pi}{4}}{2})
\end{pmatrix}\frac{1}{\sqrt{2}}(|0〉+|1〉)\\
&= \frac{1}{\sqrt{2}}\begin{pmatrix}\cos\frac{\frac{\pi}{4}}{2}-\sin\frac{\frac{\pi}{4}}{2}\\
\Big(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\Big)\Big(-\sin\frac{\frac{\pi}{4}}{2}+\cos\frac{\frac{\pi}{4}}{2}\Big)
\end{pmatrix}\\
&= \frac{1}{\sqrt{2}}\Big(\cos\frac{\frac{\pi}{4}}{2}-\sin\frac{\frac{\pi}{4}}{2}\Big)\begin{pmatrix}1 \\ \cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\end{pmatrix}\\
&= \frac{\cos\frac{\frac{\pi}{4}}{2}-\sin\frac{\frac{\pi}{4}}{2}}{\sqrt{2}}\Big(|0〉+e^{i\frac{\pi}{4}}|1〉\Big)
\end{align}
よって、ブロッホ球上の位置及び軸となす角は以下となります。
\theta=45度(\frac{\pi}{4})\\
\phi=45度(\frac{\pi}{4})
ブロッホ球の青矢印に一致することがわかりました。
以上で、量子状態の回転操作(回転計算)についての解説を一旦終了します。
次節は、python及びblueqatを使用した回転計算とプログラミングについて解説します。
 関連情報
関連情報
![]() 量子コンピュータの基本 - ブロッホ球の数式をしっかり解説
量子コンピュータの基本 - ブロッホ球の数式をしっかり解説
https://qiita.com/ttabata/items/0e839d03963d656551e0
 ご意見など
ご意見など
ご意見、間違い訂正などございましたらお寄せ下さい。