この記事の目的
量子コンピューターや量子情報を利用した量子科学計算に必須の知識であるブロッホ球について学びます。数式の裏付けも行います。
量子ビットの重ね合せの原理について
ノートパソコンやスマートフォンなど、私達が日常で使用しているコンピュータは量子コンピュータに対して古典コンピュータと呼ばれます。
古典コンピュータでは、0と1を情報の基礎単位として、この0または1(ビットと呼びます)を大量に集めて、記憶させたり、足したり引いたりなど高速に処理することで計算を行います。0と1は明確に識別され、混同したり、狂うことは許されません。
これに対して、量子コンピュータはこの0と1が混ざり合った状態を取り扱います。この0と1が混ざり合った状態を重ね合せ状態と呼びます。
混ざり合うことは古典コンピュータでは許されないため一見矛盾しているように見えますが、これは量子力学に基づいた原理の上の事象であるため物理的に(自然原理的に)は許され、さらに、量子力学を用いてこの重ね合せ状態を理解・応用することで、新たな、そしてより高度な計算技術として利用しようする試みが量子コンピュータです。
重ね合せの原理(重ね合せ状態)を式で表してみます。
0と1の2つの要素が重ね合っていて、そのうちの0が占める割合が$\alpha$で表される量、1が占める割合が$\beta$で表される量とすると、以下のように表すことができます。
|\psi〉 = \alpha|0〉 + \beta|1〉 … ①
ただし、$\alpha$、$\beta$は以下を満たす複素数です。
|\alpha|^2 + |\beta|^2 = 1 … ②
記号$|\psi〉$はプサイと読み、0と1が重ね合わされている状態を表す変数です。
すなわち、$|\psi〉$の中身が、0と1が何らかの混合状態となっている、ということです。
また、量子コンピュータや量子計算では、0を$|0〉$、1を$|1〉$と書きます。
この記号"|"と"〉"で文字を囲って書く書き方は、物理学者のP.A.M.ディラックにより考案され、Diracの表記法と呼ばれます。
記号"|"と"〉"で表現する値はケットベクトルと呼ばれます。
|\psi〉 → ケットベクトル
また、記号"〈"と"|"で表現する値はブラベクトルと呼ばれます。
〈\phi| → ブラベクトル
上記で、|0〉と|1〉のそれぞれの占める割合を「$\alpha$で表される量、$\beta$で表される量」と表現しました。
ここで、$\alpha$と$\beta$は確率ではなく、確率振幅と呼ばれます。
実際の確率は、それぞれ2乗した値となります。
|0〉が占める割合(確率) → $|\alpha|^2$
|1〉が占める割合(確率) → $|\beta|^2$
確率の原則から②が導かれます。
ブロッホ球の事前準備
ブロッホ球を学ぶ前に、以下を考えてみます。
|0〉と|1〉が重ね合された1量子ビットを以下に定義します。
|\psi〉 = cos(\theta / 2)|0〉 + e^{i\phi}sin(\theta / 2)|1〉 ... ③
冒頭では、1量子ビットを①のように書きましたが、上記の③のように書いても良いことを確認します。
③を重ね合せの原理①と比較すると、$\alpha$、$\beta$はそれぞれ以下の関係を得ます。
\alpha = cos(\theta / 2) \\
\beta = e^{i\phi}sin(\theta / 2)
オイラーの公式から、$\beta$は以下となります。
\begin{align}
\beta &= e^{i\phi}sin(\theta / 2) \\
&= (cos(\phi) + isin(\phi))sin(\theta / 2) \\
&= cos(\phi)sin(\theta / 2) + isin(\phi)sin(\theta / 2)
\end{align}
$\alpha$、$\beta$は複素数であり、それぞれの実部と虚部は以下となります。
$\alpha$の実部 … $cos(\theta / 2)$
$\alpha$の虚部 … なし
$\beta$の実部 … $cos(\phi)sin(\theta / 2)$
$\beta$の虚部 … $sin(\phi)sin(\theta / 2)$
一般に、以下のような複素数$Z$について、その大きさ$|Z|$は④の通りとなります。
Z = x + iy \\
|Z| = \sqrt{x^2 + y^2} ... ④
上記では、$x$は$Z$の実部、$y$は$Z$の虚部です。
④の性質を用いると、$|\alpha|$と$|\beta|$は以下のように計算できます。
|\alpha| = \sqrt{cos^2(\theta / 2)} \\
|\beta| = \sqrt{\big(cos(\phi)sin(\theta / 2)\big)^2 + \big(sin(\phi)sin(\theta / 2)\big)^2}
上記を用いて$|\alpha|^2 + |\beta|^2$を計算すると、
|\alpha|^2 + |\beta|^2 = \bigg(\sqrt{cos^2(\theta / 2)}\bigg)^2 + \\
\bigg(\sqrt{\big(cos(\phi)sin(\theta / 2)\big)^2 + \big(sin(\phi)sin(\theta / 2)\big)^2}\bigg)^2 \\
= cos^2(\theta / 2) + \big(cos(\phi)sin(\theta / 2)\big)^2 + \big(sin(\phi)sin(\theta / 2)\big)^2 \\
= cos^2(\theta / 2) + cos^2(\phi)sin^2(\theta / 2) + sin^2(\phi)sin^2(\theta / 2) \\
= cos^2(\theta / 2) + \big(cos^2(\phi) + sin^2(\phi)\big)sin^2(\theta / 2) \\
= cos^2(\theta / 2) + sin^2(\theta / 2) \\
=1 ... ⑤
⑤より②を導くことができました。
よって、重ね合せの1量子ビットは③のように書いて良いことが確認できました。
ブロッホ球
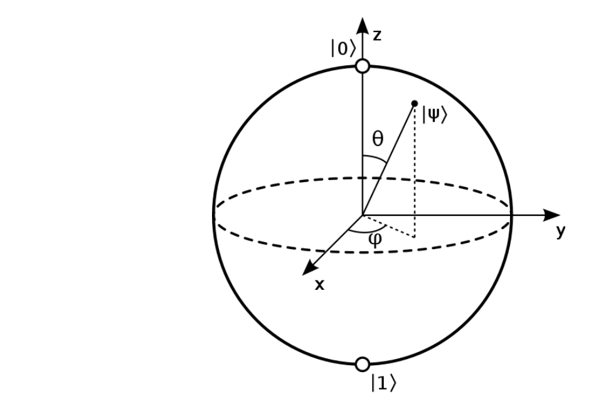
ブロッホ球(Bloch ball)は、量子ビットの状態を半径1の単位球面上の点として表したモデルです(下図)。
量子ビットの表記は前述の③を用います。特に、$\theta$と$\phi$は以下の範囲を取るものとします。
|\psi〉 = cos(\theta / 2)|0〉 + e^{i\phi}sin(\theta / 2)|1〉\\
ただし、0≦\theta≦\pi、0≦\phi≦2\pi
図の通り、北極にあたる位置が量子ビット|0〉、南極にあたる位置が量子ビット|1〉に対応します。
また、xyz3次元直交座標の原点をブロッホ球の中心に合わせたとき、$\theta$はz軸とのなす角、$\phi$は$|\psi〉$からxy平面上に下ろした垂線がとx軸となす角となります。
さらに、球面上の$|\psi〉$を3次元座標x,y,zで表した場合、$\theta$,$\phi$及びx,y,zは以下の関係があります。
x = sin\theta cos\phi \\
y = sin\theta sin\phi \\
z = cos\theta
ブロッホ球上の点と量子ビットを比較してみる
それでは、ここでブロッホ球上の点と実際の量子ビット(量子状態)の代表的ないくつかを比較してみます。
①量子ビットが|0〉の場合
量子ビット(量子状態)$|\psi〉$が|0〉の場合はブロッホ球上では以下となります。
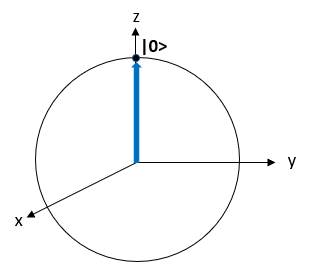
それぞれの角度$\theta$、$\phi$は0なので、$|\psi〉$は以下のようになります。
\begin{align}
|\psi〉 &= cos(0)|0〉 + e^{0}sin(0)|1〉\\
&= |0〉
\end{align}
|0〉はブロッホ球上の北極点であることから、図と式の結果は一致します。
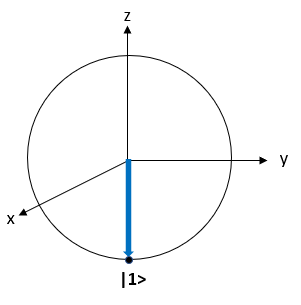
②量子ビットが|1〉の場合
量子ビット(量子状態)$|\psi〉$が|1〉となる場合を考えます。
\begin{align}
|\psi〉 &= cos(\theta / 2)|0〉 + e^{i\phi}sin(\theta / 2)|1〉\\
&= |1〉
\end{align}
これを満たす条件は、$cos(\theta / 2) = 0$、$e^{i\phi} = 1$、$sin(\theta / 2) = 1$となるため、$\theta$、$\phi$は以下となります。
\theta = \pi \\
\phi = 0
よって、ブロッホ球上では下図のように南極点を指します。
③量子ビットが$\frac{1}{\sqrt{2}}(|0〉+|1〉)$の場合
量子ビット(量子状態)が$\frac{1}{\sqrt{2}}(|0〉+|1〉)$となる場合を考えます。
\begin{align}
|\psi〉 &= cos(\theta / 2)|0〉 + e^{i\phi}sin(\theta / 2)|1〉\\
&= \frac{1}{\sqrt{2}}(|0〉+|1〉)
\end{align}
これを満たす条件は以下となります。
cos(\theta / 2) = \frac{1}{\sqrt{2}} \\
e^{i\phi}sin(\theta / 2) = \frac{1}{\sqrt{2}}
よって、上記を満たす解$\theta$,$\phi$は以下となります。
\theta = \pi / 2 \\
\phi = 0
ブロッホ球上では下図の点を指します。
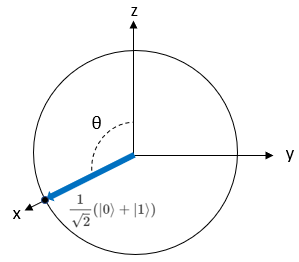
上記$\frac{1}{\sqrt{2}}(|0〉+|1〉)$は、アダマール変換を行ったときの量子状態です。つまり、|0〉と|1〉の重ね合せ状態を意味します。
関連情報
■blueqatで量子ゲートを操作し、量子もつれ（エンタングルメント）状態を生成する
https://qiita.com/ttabata/items/eb3ded49b96cb89f9a46
ご意見など
ご意見、間違い訂正などございましたらお寄せ下さい。